基于最小二乘的N-S方程算子分裂有限元法

王大国,任燕纬,沈连山,THAM Leslie George

(1.大连大学材料破坏力学数值试验研究中心,辽宁 大连 116622;2.大连大学信息工程学院,辽宁 大连 116622;3.香港大学土木工程系,香港 999077)

求解N-S方程的数值计算方法主要有有限差分法[1]、有限体积法[2]和有限元法。其中,有限元法由于适合处理复杂几何形状和边界条件而成为计算力学中的优选方法,目前已经发展了多种有限元数值计算方法,传统的Galerkin有限元法实质上采用的是中心差分格式,随着雷诺数的增大,N-S方程中的对流项越来越强,呈现强非线性特性,从而引起数值解的振荡失真。Petrov-Galerkin法(P-G法)[3]通过将权函数取为基函数的某种修正形式使计算格式具有人工耗散能力,提高了解的精度,随后发展了多种迎风方法,如流线迎风Petrov-Galerkin法(SUPG法)[4]等。许多其他近似方法也可以得到与P-G法相同的结果,如Galerkin最小二乘近似法(GLS法)[5]等。上述各方法都包含一个对原Galerkin法的耗散修正项,产生了一个包括二阶空间导数的附加项。Taylor-Galerkin有限元法(T-G法)[6]时间方向上的Taylor展开先于空间上的Galerkin离散,相比P-G法不需要使用特殊的权函数,也无需确定人工耗散自由参数来达到高精度。在T-G法的基础上发展了多种有限元法,如二阶全展开Euler-Taylor-Galerkin有限元法(ETG法)[7]、特征线Galerkin法[8]、基于Taylor展开的分步有限元格式[9]等。基于特征线的分离算法(CBS法)[10]是结合分离算法与特征线Galerkin法的一种比较新的算法。算子分裂法是Yanenko[11]在1971年提出的经典分裂法,该算法具有格式灵活、稳定性好等特点。Ying[12]采用算子分裂法求解流函数涡量形式的线性N-S方程,证明了近似解的收敛性,但未给出数值解。曹志先等[13]用算子分裂法求解Burgers方程,并分析了该算法的稳定性条件。Wang等[14]提出了CBOS方法,将N-S方程分裂成扩散项和对流项,对流项求解采用特征线Galerkin法。

本文在文献[5,11-14]的基础上,采用基于最小二乘的N-S方程算子分裂有限元法(least-squarebased operator-splitting,简称LSBOS)求解二维非定常黏性不可压缩流体N-S方程,在每个时间层上应用算子分裂技术将N-S方程分裂成扩散项和对流项,这样可以避免两种不同性质的物理过程在一起求解时计算的困难。扩散项是一个抛物线方程,时间离散采用向后差分格式,空间离散采用标准Galerkin有限元法,将其结果作为求解对流项的初值。对流项是一个双曲线方程,时间离散仍采用向后差分格式,空间离散采用最小二乘法,并且依据最小二乘法的原理直接给出权函数,避免了其他有限元法依据经验或人为选择权函数的困难。分别对方腔流和后台阶流进行数值模拟,在方腔流数值模拟中,给出了速度对比曲线,分析了时间步长和空间步长对数值模拟结果的影响;在后台阶流数值模拟中,描述了不同雷诺数下的流场特征和速度对比曲线,所得计算结果与试验结果吻合很好,说明该方法有很好的收敛性和较高的精度,认为该方法具有良好的应用前景。

1 控制方程

二维非定常黏性不可压缩流体N-S方程的无量纲形式为

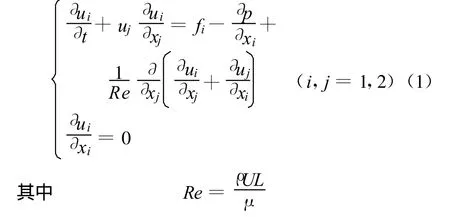
式中:(u1,u2)=(u,v),u和v分别为水平方向和垂直方向的速度;t为时间;p为压强;f1和f2分别为水平方向和垂直方向的外力;(x1,x2)=(x,y),x,y分别为水平方向和垂直方向的坐标;Re为雷诺数;ρ为流体密度;U为特征速度;L为特征长度;μ为黏性系数。

2 计算方法

2.1 算子分裂法

采用LSBOS有限元法求解式(1),计算中用算子分裂法将式(1)分成扩散项(式(2))和对流项(式(3)):扩散项

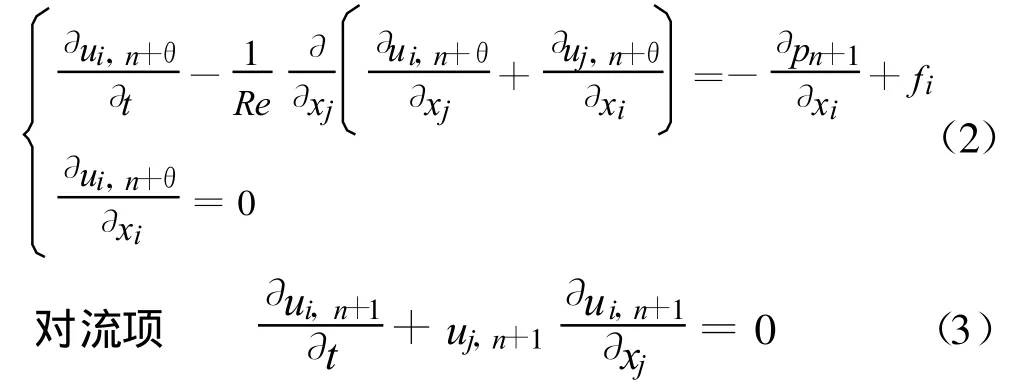
式中:ui,n+θ,uj,n+θ为扩散项(式(2))在 n+1时刻的解,同时也是对流项(式(3))在 n时刻的初值;ui,n+1,uj,n+1为对流项(式(3))在 n+1时刻的解,同时也是N-S方程(式(1))在n+1时刻的解。

2.2 对流项最小二乘法

将式(3)采用向后差分格式进行时间离散,并将ui,n+θ简记为ui:

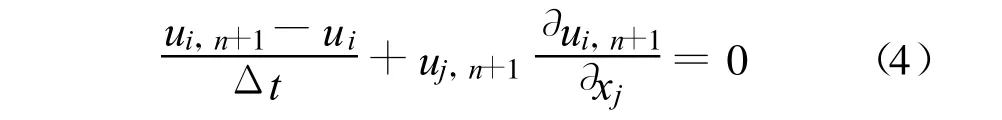
式中:Δt为计算时间步长。

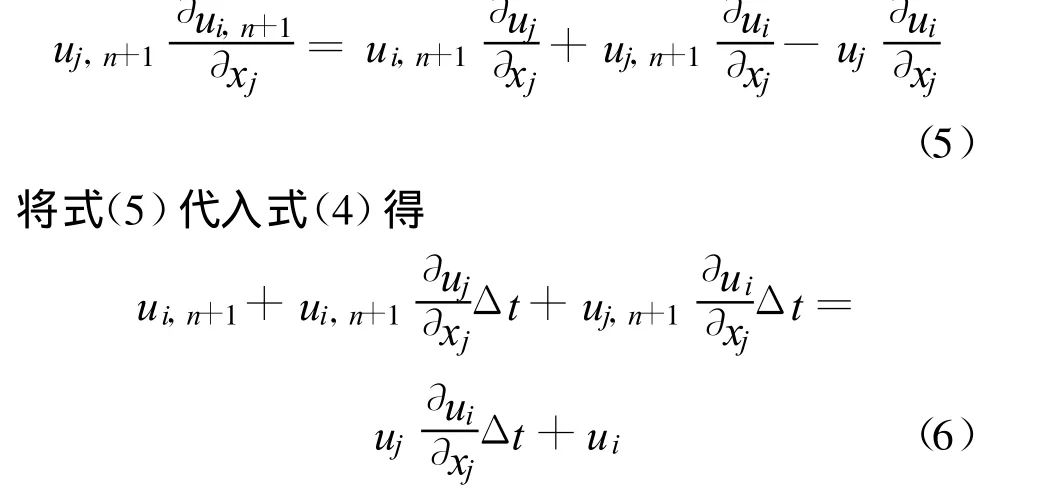
然后用最小二乘法求解式(6),其虚功方程如下:

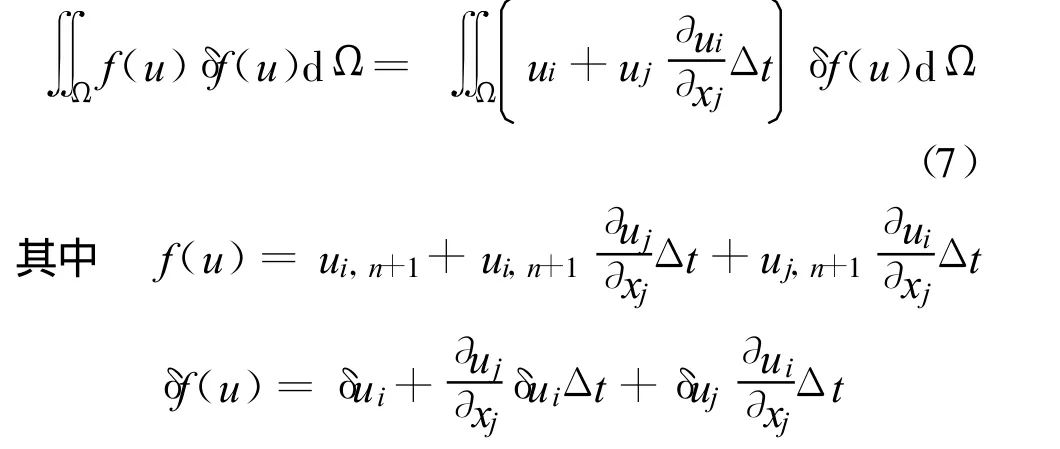
式中:Ω为求解区域;δui,δuj为虚位移。

3 有限元求解

3.1 扩散项有限元求解

扩散项有限元求解的详细推导过程与文献[14]中扩散项有限元求解的过程相同,在整个计算域合成可得总体有限元方程:

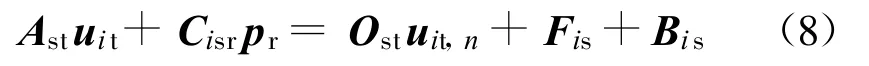
式中:Ast为速度对应的刚度矩阵;Cisr为压力对应的刚度矩阵;Ost,Fis,Bis均为载荷矩阵,具体推导参见文献[14];s,t为速度的总体节点号;r为压力总体节点号。求解式(8)可得 p和ui,n+θ。

3.2 对流项有限元求解

类似扩散项的单元分析及插值,对式(7)进行分析,得到单元有限元方程:

合成总体有限元方程:

在电商购物平台上有很大一部分不满意的评价是来自于物流配送过程中造成的快件丢失、快件破损以及快递慢递等原因，而导致这些原因的主要问题在于快递员的服务质量不过关，快递员的暴力丢件和私藏快件等都是导致快递丢件、破损的主要原因。圆通承接了电商平台很大一部分的订单，提高服务质量势在必行。

式中:D st为刚度矩阵;G i s为载荷矩阵。

求解式(10)可得式(1)在 n+1时刻的速度值ui,n+1。

4 边界条件处理及N-S方程的求解过程

4.1 边界条件处理

采用LSBOS有限元法求解N-S方程,求解过程中只需给出扩散项的边界条件。扩散项是一个抛物线方程,边界条件见第5节数值验证中的具体数值模型。

4.2 求解过程

已知n时刻的值,求解 n+1时刻的值时,N-S方程的求解过程为:①以n时刻的速度场ui,n和压力场pn作为初值,求解扩散项(式(2)),得到 n+1时刻速度场的过渡值 ui,n+θ和压力场pn+1;②以ui,n+θ作为初值,求解对流项(式(3)),得到 n+1时刻的速度场 ui,n+1,完成n+1时刻的求解;③转到下一时刻,重复步骤①和②。

5 数值验证

5.1 方腔流验证

方腔流是流体力学中用来检验数值模拟可靠性的经典算例,利用本文所建立的模型对方腔流进行数值模拟。如图1所示,方腔无量纲尺度为1×1,内部流体的初始速度和压力都是零;顶边施加无量纲速度u=1,v=0,其他三边都是固壁,施加无滑移边界条件u=0,v=0。坐标原点在方腔左下角,在该点置相对压力p=0。整个计算域划分为30×30个九节点四边形单元,共有3721个节点。

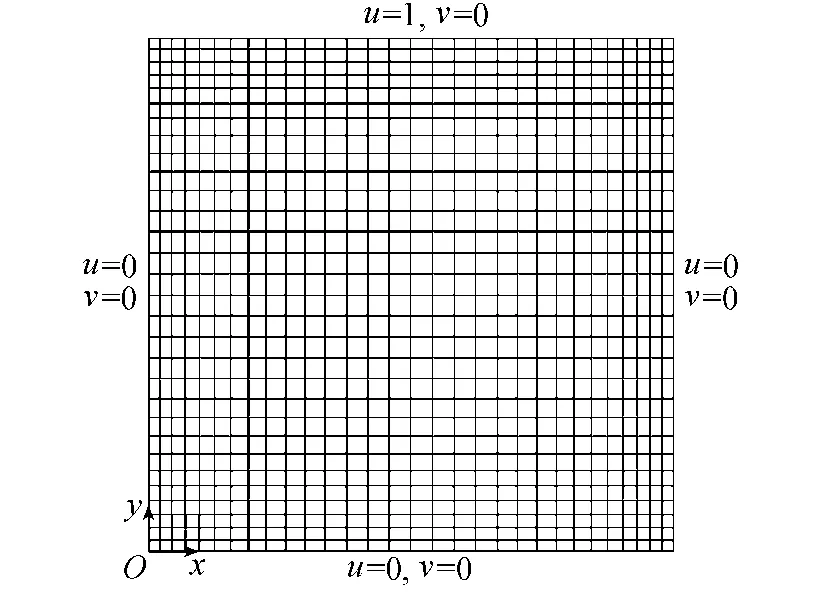
图1 方腔流几何构型和边界条件

5.1.1 不同雷诺数的影响

从图 2可以看出,本文模型计算结果与Ghia等[17]的计算结果吻合很好。本文选择的网格数为30×30,而Ghia等[17]计算的网格数为129×129,本文算法在采用较少单元数的情况下得到了较精确的结果,这表明基于最小二乘的N-S方程算子分裂有限元法具有较高的精度和很好的收敛性。

5.1.2 空间步长对计算精度的影响

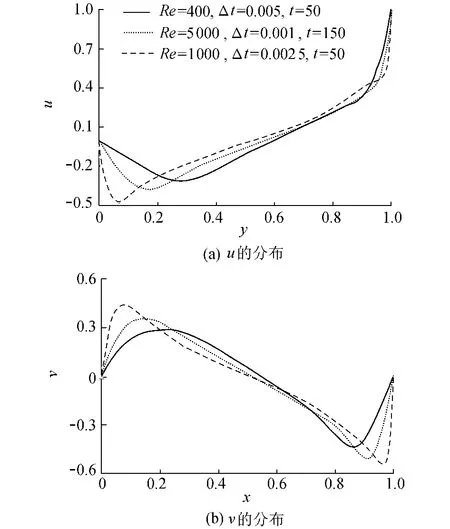
图2 不同雷诺数下速度沿中线的分布

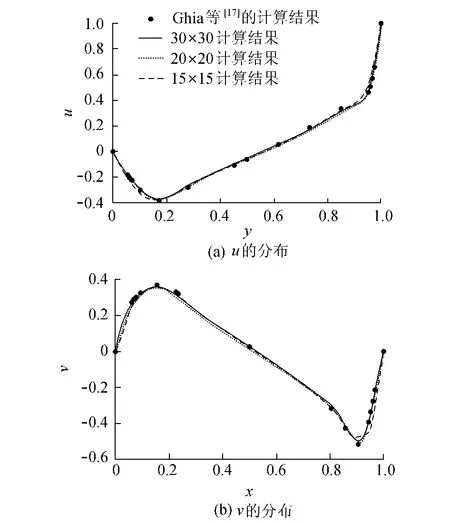
图3 Re=1000,Δt=0.0025,t=50时速度沿中线的分布

5.1.3 时间步长对计算精度的影响

图4给出了雷诺数Re=1000、计算时间t=50、网格数为30×30时不同时间步长下速度沿中线分布的对比。从图4可以看出,当 Δt=0.01时,本文计算结果与Ghia等[17]计算结果的平均相对误差绝对值为9.152%;当Δt=0.005时误差为5.476%;当Δt=0.0025时误差为2.123%。

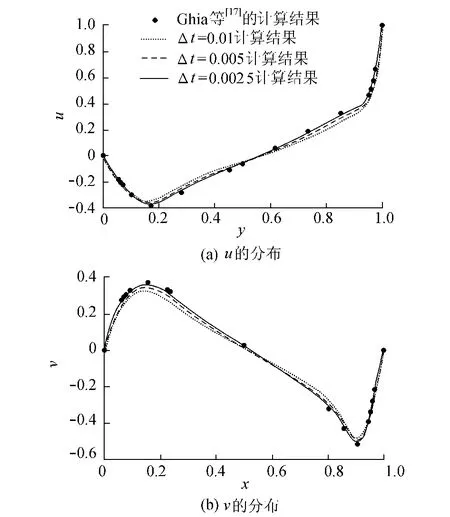
图4 Re=1000,t=50,网格数为30×30时速度沿中线的分布

5.2 后台阶流验证

后台阶流的几何构型见图5,图中H为后台阶的高度,h为入口处高度(H和h均为无量纲量),台阶长度L1=10H,台阶后长度L2=30H。入流特征速度为抛物线分布,U=k(y-H)(H+h-y)(其中k为待定常数,根据雷诺数的不同取值不同),固壁采用无滑移条件,出口边界为压力零参考面。网格单元为九节点四边形,垂直方向每单位网格长度为H/8,水平方向每单位网格长度为H/2,在台阶壁面附近进行局部网格加密。

图5 后台阶流的几何构型

5.2.1 流场特征分析

计算时取 H=1,h=H,Δt=0.005。图6给出了Re=100,500,1000下流场在 t=50时的流线。从图6(a)可以看出,低雷诺数下流线平滑,流动稳定,在台阶后方存在唯一回流区;随着雷诺数的增大,顶部出现二次回流区,见图6(b);当雷诺数继续增大时,下壁面出现三次回流区,见图6(c)。文献[18]也得到了类似的分析结果,表明本文模型能比较精确地模拟出各种雷诺数下后台阶流的流场特征。

5.2.2 速度曲线对比

为了与Armaly等[19]的试验结果进行对比,模型的几何参数与文献[19]的试验布置完全一致,取H=0.49cm,h=52H/49。图7、图8分别给出了雷诺数Re=100,389时水平速度u在不同水平位置处沿垂向剖面的分布。

图6 不同雷诺数下t=50时的流线

图7 Re=100时水平速度u在不同水平位置处沿垂向剖面的分布

图8 Re=389时水平速度u在不同水平位置处沿垂向剖面的分布

从图7、图 8可以看出,当 Re=100时,本文计算结果与试验结果吻合很好;当Re=389时,尽管个别地方计算结果与试验结果存在一定的误差,但整体上基本吻合。在计算过程中经过各个断面的流体质量最大误差不超过3%,基本保持不变,说明数值模型是守恒的。

6 结 语

本文提出了一种新的求解二维非定常黏性不可压缩流体N-S方程的算法,即基于最小二乘的N-S方程算子分裂有限元法。在每一个时间层上,应用算子分裂技术将N-S方程分裂为扩散项和对流项。扩散项采用标准Galerkin有限元法,并将其结果作为求解对流项的初值;对流项采用最小二乘有限元法。将对流项与扩散项分开求解,既能考虑对流占优特点又能兼顾方程的扩散性质,同时可以避免在整个计算域求解大规模非线性方程组。对流项采用最小二乘避免了其他有限元法选择权函数的困难。对方腔流进行了数值模拟,计算结果与标准解吻合很好,分析了空间步长和时间步长对数值模拟结果的影响,得出空间步长对计算结果的影响较小,即在较大空间步长情况下也能取得较满意的计算结果。同时对后台阶流也进行了数值研究,描述了不同雷诺数下的流场特征和速度对比曲线,所得计算结果与试验结果吻合较好,表明本文提出的算法具有较好的收敛性和较高的精度。

[1]DOUGLAS J,RUSSELL T F.Numerical methods for convection-dominated diffusion problems based on combining the method of characteristics with finite element or finite difference procedures[J].SIAM Journal on Numerical Analysis,1982,19(5):871-885.

[2]SYLVAIN B,FLORENT C,JEAN-MATE H.A finite volume method to solve the Navier-Stokes equations for in compressible flows on unstructured meshes[J].Int J Them Science,2000,39:806-825.

[3]CHRISTIE I,GRIFFITHS D F,MITCHELL A R,et al.Finite element methods for second order differential equations with significant first derivatives[J].International Journal for Numerical Methods in Engineering,1976,10:1389-1396.

[4]BROOKS A N,HUNGHES T J.Streamline upwind/preov Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations[J].Computer Methods in Applied Mechanics and Engineering,1932,32(1/2/3):199-259.

[5]HUNGHES T J,FRANCA L P,HULBERT G M.A new finite element formulation for computational fluid dynamicsⅧ:the Galerkin least-squares method for advective-diffusive equations[J].Computer Methods in Applied Mechanics and Engineering,1989,73(2):173-189.

[6]DONEA J.A Taylor-Galerkin method for convective transport problems[J].International Journal for Numerical Methods in Engineering,1984,20:101-119.

[7]王小华,樊洪明,何钟怡.后台阶流动的数值模拟[J].计算力学学报,2003,20(3):361-365.

[8]MORTON K W.Generalised Galerkin methods for hyperbolic problems[J].Computer Methods in Applied Mechanics and Engineering,1985,52(1/2/3):847-871.

[9]JIANG C B,KAWAHARA M,KASHIYMA K.A Taylor-Galerkin-based finite element method for turbulent flows[J].Fluid Dynamic Research,1992,9:165-178.

[10]ZIENKINEWICZ O C,TAYLOR R L.The finite element method:fluid dynamics[M].5th edition.Oxford:Butterworth Heinemann,2000.

[11]YANENKO N N.The method of fractional steps[M].Berlin:Springer-Verlag,1971.

[12]YING Long-an.Viscosity splitting method in bounded domains[J].Science in China:Series A,1989,32(8):908-921.

[13]曹志先,魏良琰.用算子分裂法解Burgers方程[J].武汉水利水电学院学报,1991,24(2):193-201.

[14]WANG Da-guo,WANG Hai-jiao,XIONG Ju-hua,et al.Characteristic-based operator-splitting finite element method for Navier-Stokes equations[J].Science in China:Series E,2011,54(8):2157-2166.

[15]李庆扬,王能超,易大义.数值分析[M].4版.北京:清华大学出版社,2001.

[16]章本照.流体力学中的有限元方法[M].北京:机械工业出版社,1984.

[17]GHIA U,GHIA K N,SHIN C T.High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J].Journalof Computational Physics,1982,48:387-411.

[18]王兵,张会强,虞建丰,等.后台阶分离流动中大涡结构演变的数值模拟[J].力学季刊,2003,24(2):166-173.

[19]ARMALY B F,DURST F,PEREIRA J C F,et al.Experimentaland theoretical investigation of backward-facing step flow[J].Fluid Mech,1983,127:473-496.