水电站虹吸式进水口工作过程CFD模拟==pdf英文空格显示有误

2012-05-03侯才水王志寰

水利水电科技进展 2012年4期

侯才水,陈龙,王志寰

(1.福建水利电力职业技术学院水利工程系,福建永安 366000;2.武汉大学水资源与水电工程科学国家重点实验室,湖北武汉 430072)

虹吸是一种复杂的非稳态多相流现象,在流体机械、给排水、水处理、医学等各个领域均有广泛的应用。水电站虹吸式进水口是虹吸现象在水利工程中应用的一种重要形式,具有结构简单、运行稳定、操作方便、投资少、效益高且水流泥沙含量低等优点,特别适用于多泥沙河流上的小型水电站和泵站。虹吸式进水口设计是否合理取决于两个标准:一是形成真空所需时间短;二是虹吸破坏时断流过程安全可靠。

目前,水电站虹吸式进水口设计研究的方法主要是理论分析结合工程经验和模型试验,应用数值模拟方法对其工作过程进行研究的例子相对较少。文献[1-4]针对虹吸理论及其工程应用进行研究;文献[5-7]依据流体力学知识和以往工程经验,考虑自身工程的具体情况,设定了虹吸式进水口的体型和参数;文献[8]总结了确定虹吸式进水口结构形式、主要参数、流道尺寸、进水口淹没深度和渐变段形式等方面的注意事项和经验公式;文献[9]通过模型试验分析了几种方案下虹吸道内的流态;文献[10]通过模型试验,探讨了虹吸式进水口工作过程中的水力特性,总结了若干试验公式。理论计算不能得到非恒定两相流不同位置处的压强和流速,经验公式往往引入较大的安全度,增加了工程量,而模型试验费时费力且存在比尺效应问题[11],CFD模拟可有效弥补上述研究手段的不足。

本文应用CFD软件Flow 3D对水电站虹吸式进水口的虹吸形成过程(含抽真空过程)和虹吸破坏过程两个关键过程进行模拟研究,得到虹吸管道内压强、流速、水气界面的分布和变化情况,为虹吸式水电站的设计研究及安全稳定运行提供依据。

1 数学模型及计算方法

1.1 湍流模型

目前工程中应用最广泛的湍流模型是RANS k-ε模型,其计算量适中且精度较高。考虑到虹吸式进水口工作时水流流线弯曲程度较大且存在高应变率的流动,采用RNG k-ε湍流模型进行三维模拟,其对应的湍动能k和耗散率ε输运方程分别为[12]

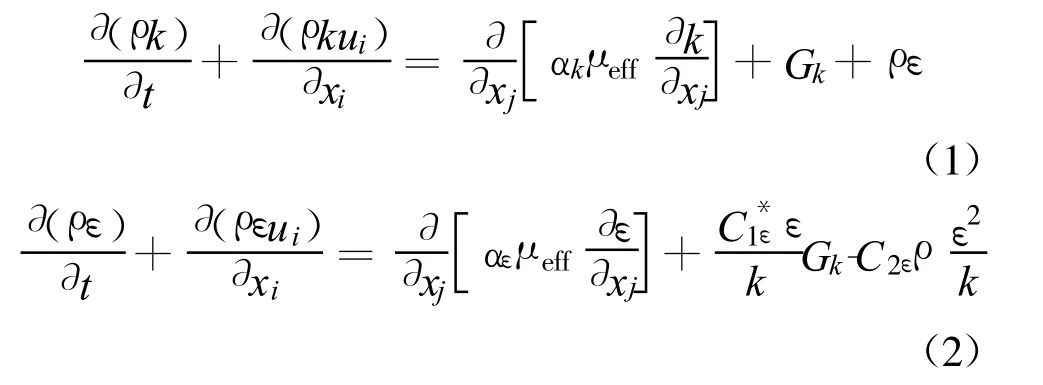
式中各符号含义见文献[12]。

1.2 自由面追踪

针对虹吸管道内水、气两相相互作用,采用VOF方法[13]追踪自由水面,定义 αa和 αw分别为计算域内空气和水的体积分数,αw=1表示该单元完全被水充满;αw=0表示该单元完全被气充满;0＜αw＜1表示该单元存在自由液面,部分是水,部分是气。

确定水和气的界面可以通过求解以下关于 αw的连续方程来实现:

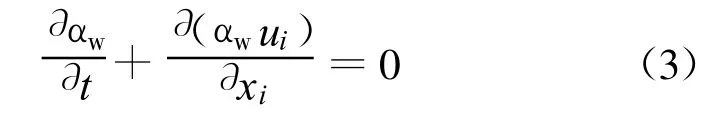
水相和气相有共同的流速场和压力场,但湍流模型中的密度和分子黏性系数则按体积分数加权确定:

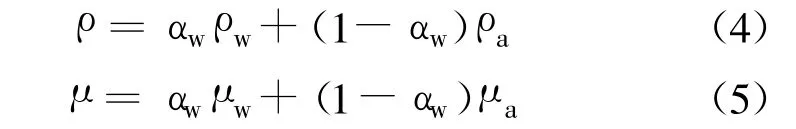
式中:ρw和 ρa分别为水和空气的密度;μw和 μa分别为水和空气的分子黏性系数。

1.3 求解方法及主要参数

采用Flow 3D软件进行计算,离散方程格式为一阶迎风格式,在非恒定湍流条件下采用压力基隐式求解。由于是虹吸现象,考虑重力作用,其值为9.8m/s2。因水、气相互作用故为两相流,流体为20℃的水,空气温度为15℃,边壁条件无滑动。

2 虹吸式进水口工作过程分析

2.1 计算条件

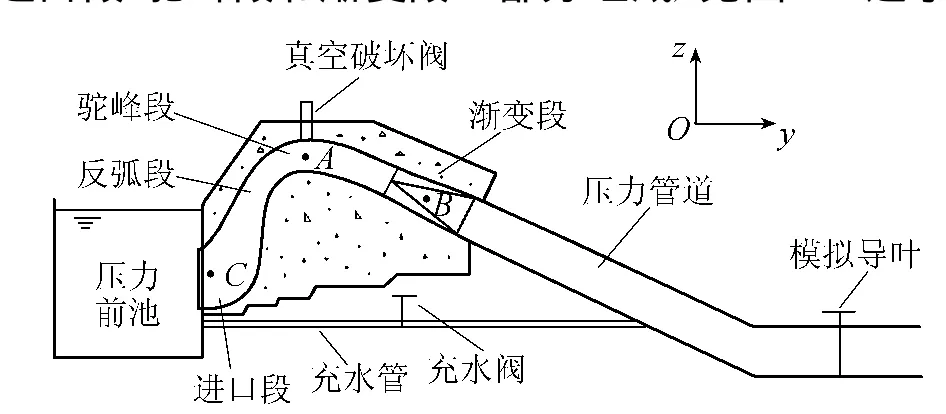
图1 虹吸式进水口结构示意图

a.计算体型。某虹吸式进水口电站设计水头为16 m,引水流量为12m3/s。虹吸式进水口流道由进口段、驼峰段和渐变段三部分组成,见图1。进水口矩形断面尺寸为2.6m×2.3 m(宽×高,下同),驼峰顶部矩形断面尺寸为2.6 m×1.2m,驼峰两侧的倾角分别为60°和45°,因此驼峰的转弯夹角为105°。驼峰断面中心的转弯半径为2m,进口段与驼峰段之间采用反弧段连接。压力管道断面为圆截面,其内径为1m,驼峰段与压力管道之间采用由矩形渐变为圆形的渐变段衔接,其长度为6.45m。

b.网格划分。因虹吸管体型在x方向上对称,故只取一半进行分析,并采用结构化六面体网格。由于虹吸管形状不规则且边界条件不同,故将计算域划分3个区块,其中区块1模拟进口段及反弧段,区块2模拟压力管道,区块3模拟压力前池,见图2。总有效网格数约为475000个。

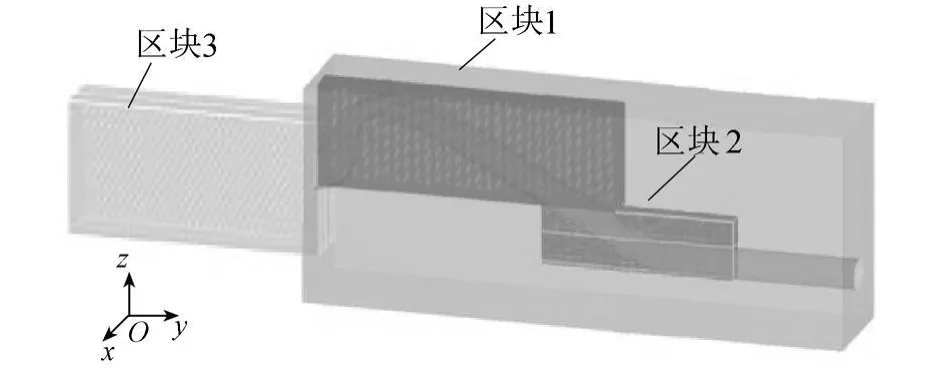
图2 网格划分示意图

c.边界条件。压力前池顶部为压力边界,水位为10.9m,压力为0Pa;抽气管和压力管道端部为速度边界,根据具体模拟工况给定速度值;其他边界为默认的对称边界条件。

d.流体参数。虹吸式进水口工作过程模拟涉及水、气两相流,且需要考虑流体的压缩性,设水的压缩性系数为5×10-10,空气的压缩性系数为1×10-5。

e.流场初始化。初始状态时水轮机导叶关闭,压力前池水位保持不变;打开充水阀,压力前池通过充水管向压力管道充水,直至水位与压力前池内水平齐平;关闭充水阀,水流静止不动。选择驼峰断面A点、渐变段B点、进口断面C点作为监测点,用于分析局部点的水力特性。A,B,C三点均位于虹吸管对称剖面上,其坐标、位置如图1所示。

2.2 抽真空过程

a.抽真空过程水面变化。虹吸管中黑色表示水,白色表示空气(下同),见图3。在 t=0 s时反弧段和压力管道内水位齐平;随着驼峰顶部空气不断被抽走,在上下游压强差和驼峰处真空吸力的作用下水面不断上升,t=180 s左右时反弧段的水体越过驼峰产生堰流;t=225 s时驼峰两侧水体液面齐平;t=300s时空气基本被抽净;此后抽气速度逐渐减为零,抽真空任务完成。同时,随着抽气的进行,驼峰处负压的绝对值不断增大,t=300 s时驼峰顶部负压值达到最大,空气抽净后该处负压值基本稳定。

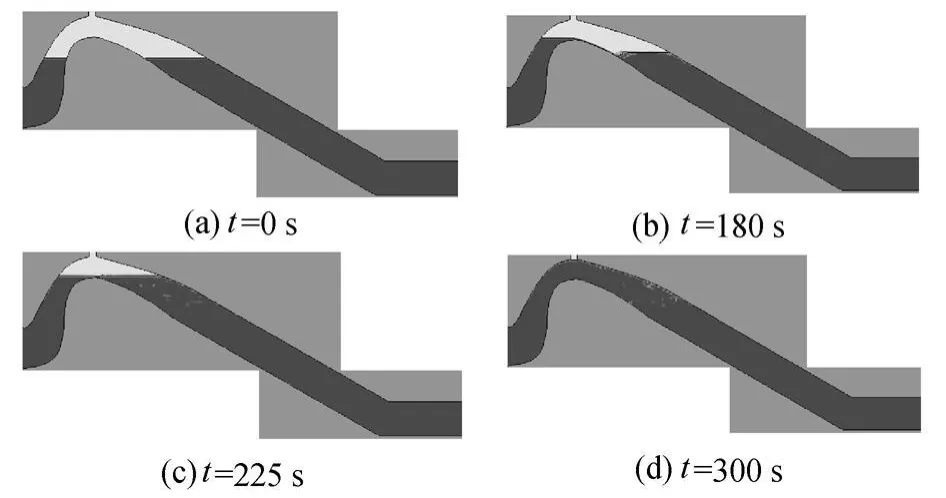
图3 抽真空过程水面变化

b.局部点压强变化过程。抽真空过程中驼峰断面A点处的压强水头逐步减小,当空气被抽净后压强水头趋于稳定,且在抽气速度减至零的过程中,压强水头基本不变,最终稳定在-1.70m左右,见图4(a)。渐变段B点处的压强水头先变小后变大,因为该点最初处于空气中,随着抽真空的进行,空气压强逐渐减小;180 s后该点处于水中,水位不断上升,压强水头逐渐增大;300 s后空气基本被抽净,该点的压强水头稳定在-0.50m左右;650～660s内抽气速度逐渐减为零,该点的压强水头基本不变,见图4(b)。

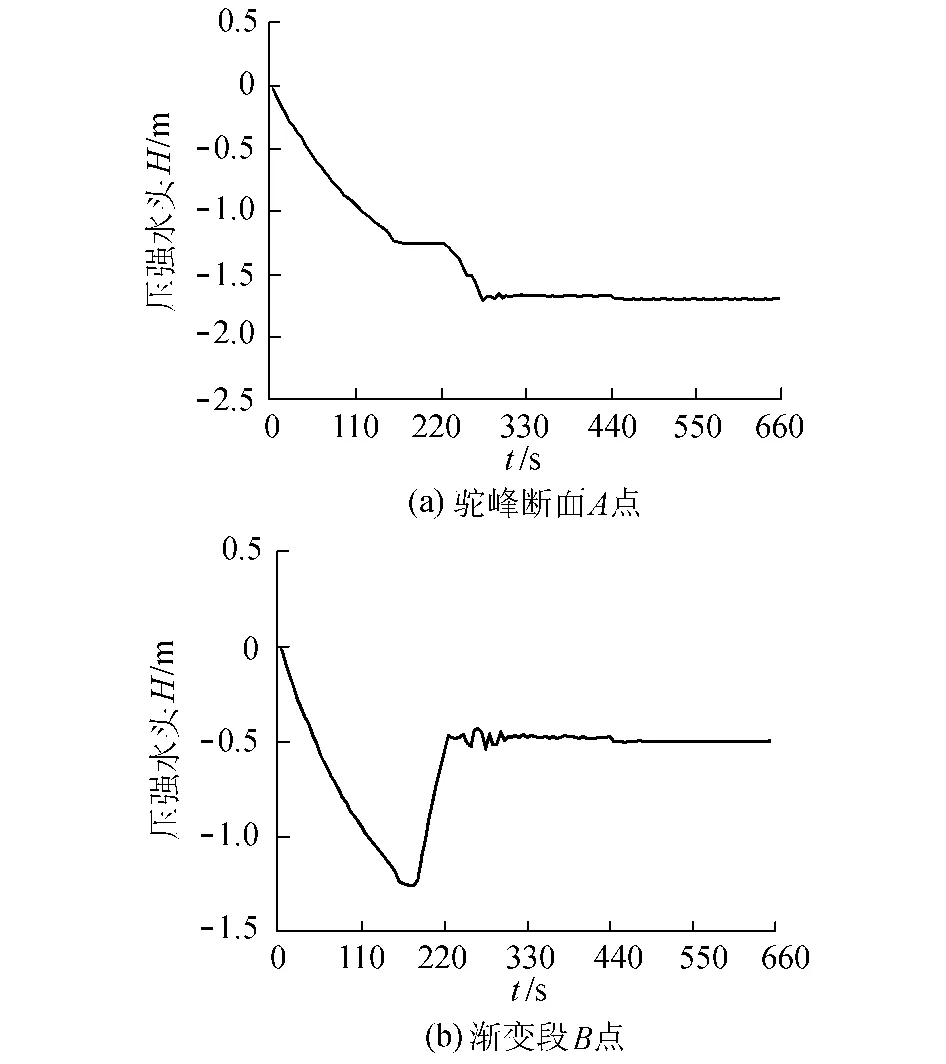
图4 抽真空过程局部点压强水头变化过程

c.局部点流速变化过程。因驼峰断面A点在270s时浸入水中,故270s之前为空气流速,之后为水的流速。在120～450s之间A点流速波动较大,随着抽真空的进行,于500s左右时vAy逐渐稳定在0.045m/s,vAz逐渐稳定在0.060m/s。抽气速度减为零后(660 s后),vAy和vAz也减为零,见图5(a)。渐变段 B点在180 s后浸入水中,120～450 s之间B点流速波动较大,随着抽真空的进行,渐变段内水体流动逐渐稳定并缓慢停止,vBy和vBz在500s之后接近零,见图5(b)。

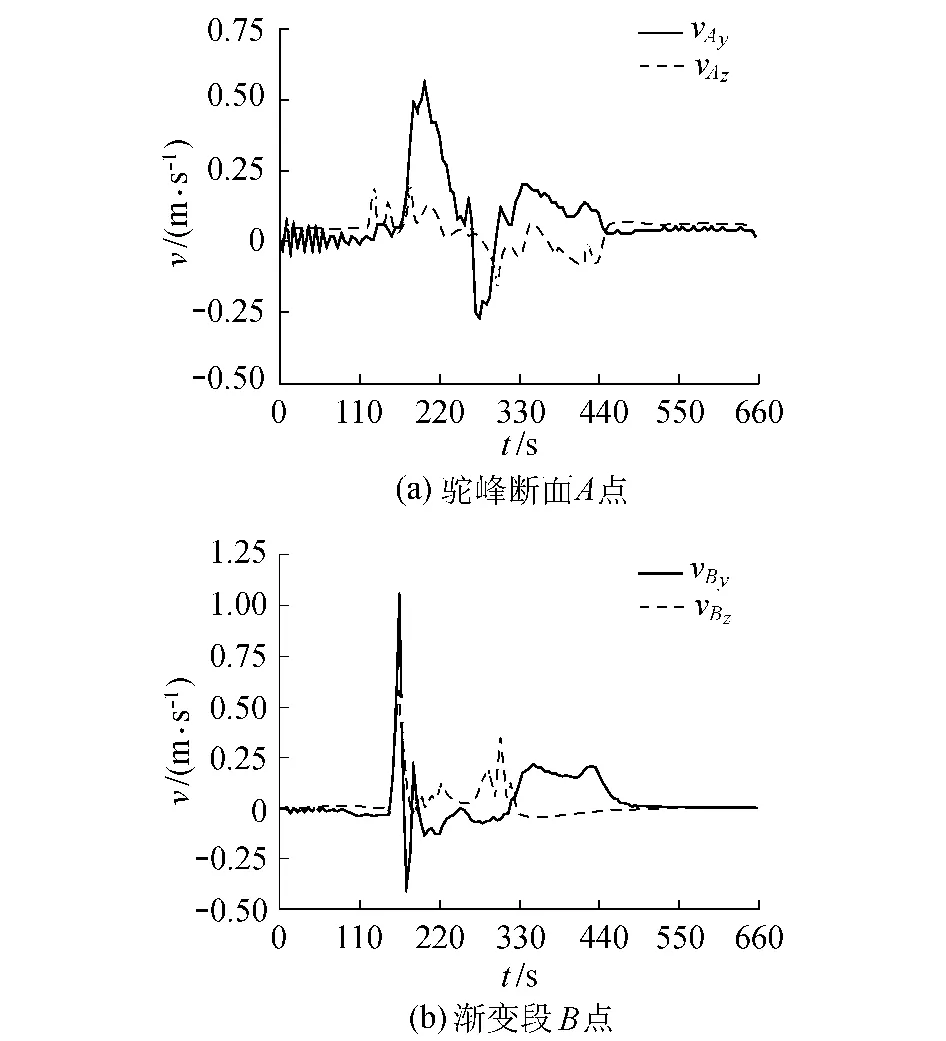
图5 抽真空过程局部点流速变化过程

2.3 虹吸形成过程

抽真空完成后封闭驼峰顶部,开启水轮机导叶,以抽真空结束状态为计算初始条件。为使虹吸迅速形成,且与水电站实际运行情况相符,将计算域中压力管道端部设为流速出口,出口流速由零逐渐增加到1.6 m/s,然后以这一速度出流;其他边界条件不变,计算体型和网格划分情况也不变。

a.局部点压强变化过程。虹吸形成过程中驼峰断面A点、渐变段B点处的压强水头起初波动较大,随着计算域内水体运动渐趋恒定,波动逐渐平稳,最后A点压强水头稳定在-1.863 m左右,B点压强水头稳定在-0.665m左右,见图6。

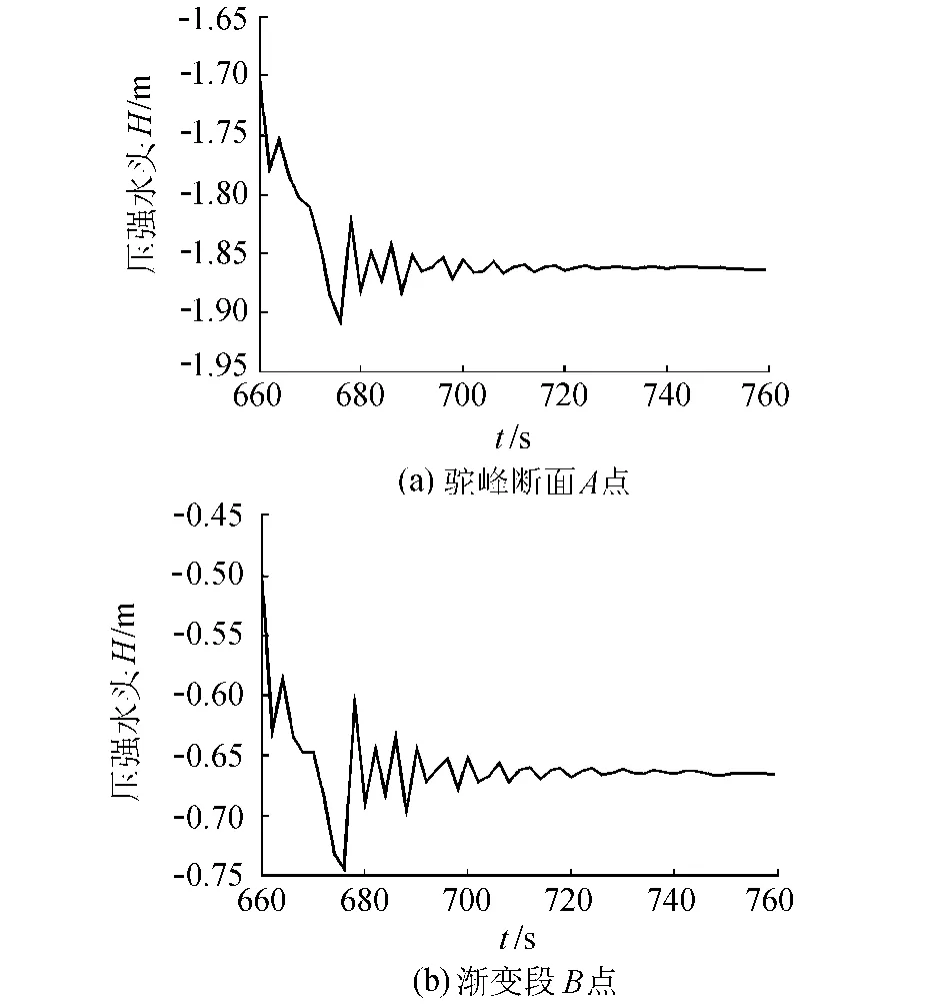
图6 虹吸形成过程局部点压强水头变化过程

b.局部点流速变化过程。当t=660 s时抽气速度为零,整个计算域内的水体几乎静止,A点和B点处的流速约为零;当t=660～676 s时随着压力管道端部流速逐渐增大,A点和B点处的流速也逐渐增大,700 s后流场基本稳定。最后,vAy稳定在1.71m/s,vAz稳定在0.25m/s,即 A点的流速约为1.73m/s;vBy稳定在1.44m/s,vBz稳定在-0.70m/s,即B点的流速约为1.60m/s,见图7。

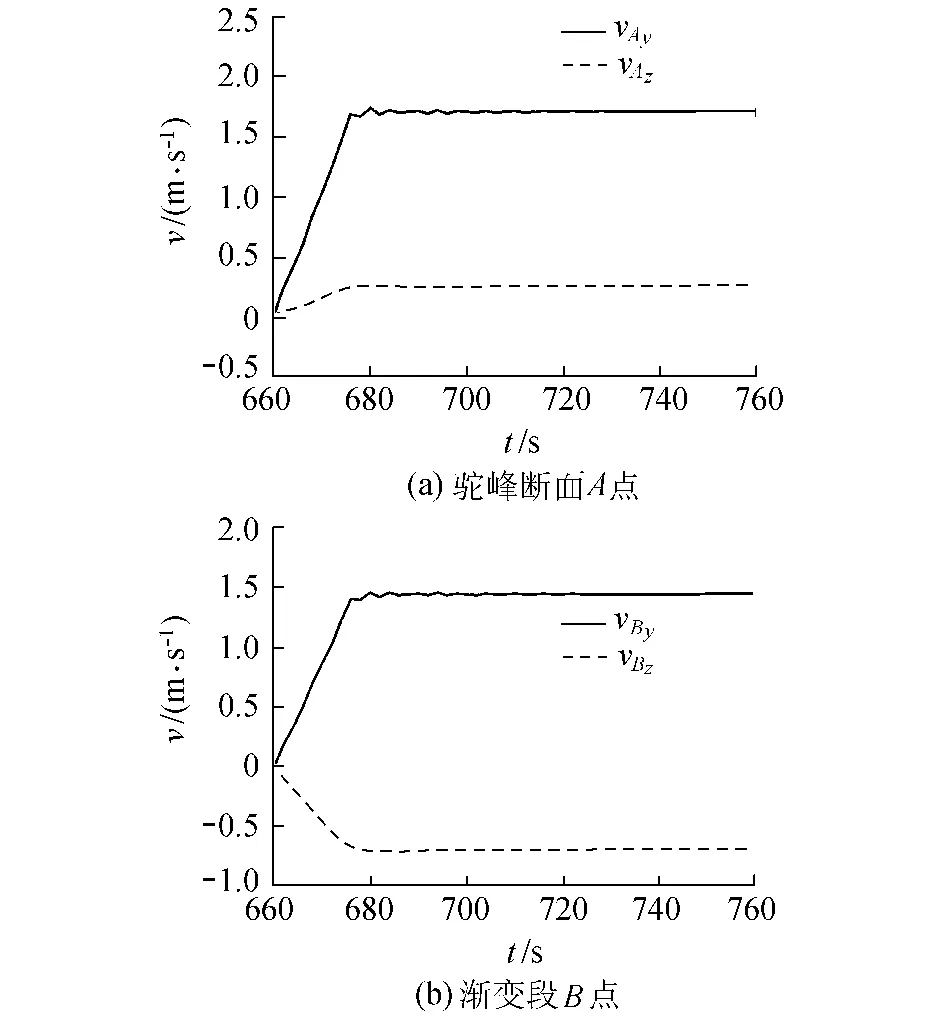
图7 虹吸形成过程局部点流速变化过程

2.4 虹吸破坏过程

虹吸形成后关闭压力管道端部,同时打开真空破坏阀让空气进入,从而使虹吸破坏。以虹吸形成后的稳定状态为计算初始条件,真空破坏阀处设为压力边界,压力管道末端设为流速边界,其他边界条件不变,计算体型和网格划分情况也不变。

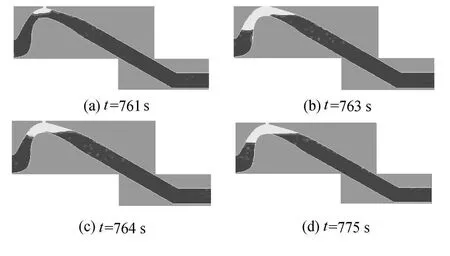
图8 虹吸破坏过程水面变化

a.虹吸破坏过程水面变化。t=760 s时压力管道末端流速开始减小,真空破坏阀打开,此时进水口内仍充满水;t=761 s时空气从真空破坏阀进入驼峰段,进水口内的水体在重力作用下开始下降,见图8(a);t=763 s时由于驼峰顶部真空度减小,渐变段和压力管道内的水向反弧段溢出,在重力作用下反弧段水位下降至最低点,见图8(b);t=764 s时由于压力前池的反射作用,反弧段水位上升至高于压力前池水位的位置,压力管道端部流速逐渐减为零,见图8(c);此后,反弧段水体不断波动并在t=775 s后渐趋稳定在压力前池水位高程,渐变段和压力管道内水体逐渐静止,水位稳定,见图8(d)。可见,整个虹吸进水口断流时间很短(大约15 s),断流迅速。

b.局部点压强变化过程。在虹吸破坏过程中渐变段B点处的压强水头在775 s后经过短暂波动便渐趋平稳,最后稳定在0.55m,见图9(a)。进口断面C点处的压强水头则不断波动,这是因为反弧段水体不断上下波动所致;随着反弧段水体波动逐渐减弱,进口段压强趋于稳定,C点压强水头稳定在2.80m,见图9(b)。

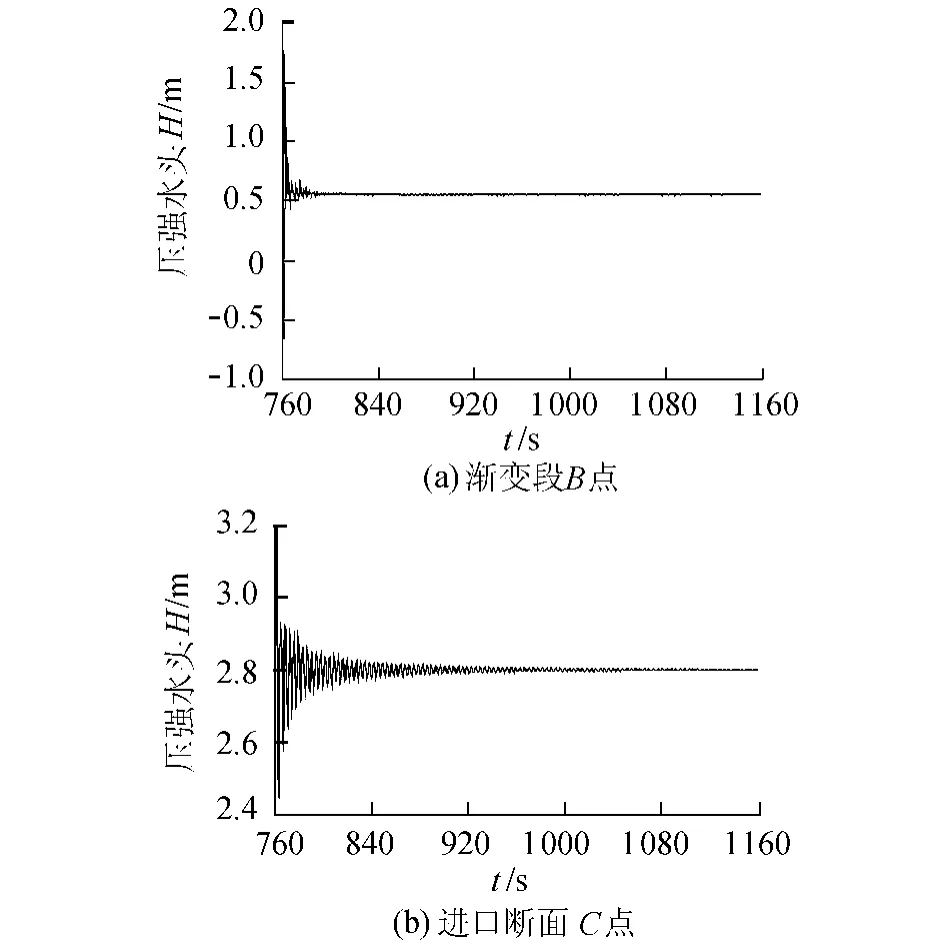
图9 虹吸破坏过程局部点压强水头变化过程

3 结论

a.在虹吸式进水口工作过程中,驼峰顶部的压强值最低。陈革强等[3]认为驼峰顶部最大真空度出现在整根虹吸管形成正常流速后,即虹吸稳定后。但实际模拟过程中,笔者发现驼峰顶部真空度在抽真空之后经过一段时间的波动才达到恒定值,即文献[3]所认为的“最大真空度”,因而实际最大真空度出现在虹吸稳定前的某一时刻,其数值与恒定值存在一定偏差,在具体工程设计过程中应加以考虑。

b.抽真空速度与压力波动幅度成正比。为了保证压力波动不至于过大,抽真空速度应加以控制。虹吸稳定后,真空度的恒定值由虹吸高度(驼峰顶部高程与压力前池水位之差)和驼峰前管段中的水头损失共同组成。

c.虹吸破坏后驼峰两侧水体平稳性存在较大差异。虹吸破坏阶段空气由真空破坏阀进入驼峰后驼峰左侧(反弧段)水体在压力前池水位所在高程附近振荡,需较长时间达到平稳;驼峰右侧(渐变段和压力管道)水体在压力管道关闭后的较短时间内达到平稳,虹吸破坏时间只需数十秒。

[1]李百齐.虹吸管出水断流装置的流体力学相似分析[J].船舶力学,2003,7(5):39-44.

[2]袁乃荣.虹吸现象的新解释[J].物理教学探讨,2001,19(5):5-6.

[3]陈革强,施俊跃,卢健国,等.水库虹吸管驼峰真空度机理分析与控制[J].水利技术监督,2008(4):50-51,73.

[4]董毅,汤正军,田明云.虹吸式轴流泵站抽真空启动探讨[J].水泵技术,2000(1):32-33.

[5]黄煌.虹吸式进水口在三坝水电站技改工程中的应用[J].中国农村水利水电,2005(9):78-82.

[6]潘正林,程云峰.中低水头引水式电站采用虹吸式进水技术[J].小水电,1996(1):21-25.

[7]沈晓燕.须江水电站虹吸式进水口的设计[J].浙江水利科技,2000(4):40-41.

[8]韩伯鲤.水电站虹吸式进水口的设计与分析[J].武汉水利电力学院学报,1980(4):35-42.

[9]黄智敏,朱红华,陆汉柱,等.虹吸溢洪道水力特性试验研究[J].湖北水力发电,2002(3):30-33.

[10]顾谦甫,卞祖铭.水电站虹吸式进水口试验研究[J].浙江水利科技,1985(2):1-4.