并行遗传算法在器件模型参数提取中的应用
2012-04-29宋文斌
宋文斌


摘要:器件的模型和模型参数提取是电子设计自动化(EDA)领域的关键工作。采用遗传算法进行器件模型参数提取工作是近年来兴起并被广泛使用的一种参数提取方法。本文讨论了并行遗传算法的特点,针对遗传算法自身的耗时问题,提出了基于MPI的主从式遗传算法,并证实了并行计算在参数提取工作中的可行性。该方法简单易用,显著提升了MOS器件模型参数提取的速度。
关键词:MOS器件;模型参数;参数提取;器件模型
1 引言
器件的模型和模型参数提取是电子设计自动化(EDA)领域的关键工作[1]。采用遗传算法进行半导体器件模型参数提取是近年来兴起并被广泛使用的一种参数提取方法[2-3]。遗传算法全局搜索能力强、不需进行繁琐的求导运算,不依赖参数初始值等特点,理论上来说只要有足够的迭代次数种能找到最优解[4]。但是,由于遗传算法是一种搜索类算法,较之传统的基于梯度进行迭代计算的解析算法, 每进行一次迭代所需要的时间较长,计算量有了显著增加, 而且对许多复杂问题而言,例如采用的全局优化策略提取复杂模型的大量参数时,标准遗传算法的求解效果往往不是解决这个问题的最有效的方法,必须对算法进行修改与优化,这些因素无疑大大增加了遗传算法的计算量,为此必须考虑算法的耗时问题。本文针对遗传算法自身的耗时问题,讨论了并行遗传算法的特点,并以主从式遗传算法为例,证实了并行计算在参数提取工作中的可行性。
2 并行遗传算法
为了有效的解决遗传算法(GA)在模型参数提取过程中的耗时问题, 提高GA的运行速度,采用并行遗传算法(PGA)是提高搜索效率的方法之一。并行遗传算法[5-6]主要有主从式并行遗传算法、粗粒度并行遗传算法和细粒度并行遗传算法。
2.1 全局PGA模型-主从式模型(master-slave model)
如图1所示,主从式模型分为一个主处理器(master)和若干个从处理器(slaves)。主处理器监控整个染色体种群,并基于全局统计执行选择等全局操作;从处理器接收来自主处理器的个体进行适应度评估等局部操作,再把计算结果传给主处理器。
主从式模型的优点是简单,保留了串行GA 的搜索行为,对计算机体系结构没有严格要求,适合运行在共享存储和分布式存储的并行计算机上。如果适应度估值操作比其他遗传算子计算量大的多时,这是一种非常有效的并行化方法。
2.2 粗粒度PGA模型-分布式模型(distributed model)
该模型又称分布式、MIMD、岛屿模式遗传算法模型。在处理器个数较少的情况下,我们可以将群体分为若干个子群体,每个子群体包含一些个体,每个子群体分配一个处理器,让它们相互独立地并行执行进化。为了防止子群体早熟,每经过一定的间隔(即若干进化代),各子群体间会交换部分个体以引入其他子群体的优秀基因,丰富各子群体的多样性。除了基本的遗传算子外,粗粒度模型引入了“迁移”算子,负责管理区域之间的个体交换。如图2所示,通常存在两种迁移实现:岛屿模型、踏脚石模型。
2.3 细粒度PGA模型-分散型 (fine-grained model)
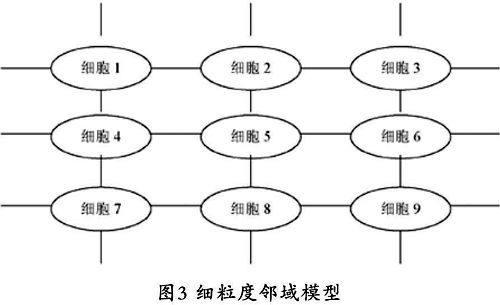
细粒度模型又称为邻域模型(neighborhood model)或细胞模型(cellular model)模型。如果并行计算机系统的规模很大,理想情况下处理器多到可以与染色体一一对应,则我们可以将每个个体分配一个处理器,让它们相互独立地并行执行进化,这样就能获得并行遗传算法的最大可能的并发性。如图3所示,在细粒度模型中,通常处理器被连接成平面网格(grid),每个处理器上仅分配一个个体,选择和交叉只在网格中相邻个体之间进行,所以网格上的邻域关系就限定了个体空间上的关系。由于对处理器数量的要求很高,所以细粒度模型的应用范围不广。
3 基于MPI的主从式遗传算法的的实现
3.1 总体构想
我们采用的主从式并行模型分为一个主处理器(master)和若干个从处理器(slaves)。主处理器监控整个染色体种群,并基于全局统计执行选择等全局操作;从处理器接收来自主处理器的个体进行适应度评估等局部操作,再把计算结果传给主处理器,其个体的分配过程是这样的:假设种群规模为N, 优化模型参数变量个数为M。适应度评估时,程序传给评价函数N个长度为M的向量。并行的任务是master处理器将这个N个长度为M的向量平均分配到各slaves处理器做适应度计算,计算结束后,评价函数返回N个适应度给master处理器。计算各处理器分得的染色体个数的方法是,首先计算出每个处理器至少分配到的染色体个数为AveNum=N/Size,如果处理器个数不能整除行数,这样将有部分处理器分得到(AveNum+1)个染色体,规定多余的染色体分配到编号小的处理器上。
3.2 并行中的消息传递机制
另外,需要注意的是,仅仅依靠例如C,C++,java等编程语言所编写的程序是无法实现上面叙述的染色体在各处理器之间的传递任务。因为,在并行计算环境中,每个进程均有自己独立的地址空间,一个进程不能直接访问其它进程中的数据,因而,在进行并行计算的任务之间进行的数据传输必须通过消息传递机制。消息传递机制,是指用户必须显式地通过发送和接收消息来实现处理器之间的数据交换。
本文采用的是MPI(Massage Passage Interface)消息传递接口。MPI是一个很好的数据传递软件平台,可以通过调用MPI库函数来进行进程调度以及任务间的通信。它实际上是一个消息传递函数库的标准说明,吸取了众多消息传递系统的优点,是目前国际上最流行的并行编程环境之一,其特点是通用性强(只要求网络支持TCP/IP网络协议)、系统规模小、技术比较成熟。本文通过调用MPI的库程序来达到程序员所要达到的并行目的,使异构的计算机群体作为一个紧凑、灵活、经济的计算机资源来使用的并行环境。
3.3 共享内存多处理器主从式并行环境搭建
全局并行化模型并不限定计算机体系结构,它可以在共享内存和分布式内存计算机中高效实现。现在简单介绍一下两种并行编程的方法:分布式内存方法和共享式内存方法。
对于分布式内存的并行计算机,各个处理器拥有自己独立的局部存储器,不存在公用的存储单元,显然,这种方法的问题就产生于分布式内存的组织。由于每个节点都只能访问自己的内存,如果其他节点需要访问这些内存中的数据,就必须对这些数据结构进行复制并通过网络进行传送,这会导致大量的网络负载。他的优点是拥有很好的扩展性,有利于快速构造超大型的计算系统。
在共享内存多处理器计算机中构成并行环境,在共享式内存方法中,内存对于所有的处理器来说都是通用的。这种方法并没有分布式内存方法中所提到的那些问题。而且对于这种系统进行编程要简单很多,因为所有的数据对于所有的处理器来说都是可以使用的,这与串行程序并没有太多区别。这些系统的一个大问题是扩展性差,不容易添加其他处理器。
为了在微机环境下使用MPI构成分布式内存并行环境,只要将PC机联接局域网,然后在每台PC机上安装相应操作系统,并安装MPI软件包即可。分布式内存即种群被一个处理器存储。这个主处理器负责将个体发送给其它从处理器进行评估,并收集计算结果,进行遗传操作来生成下一代。
对于本文所采用的在共享内存多处理器计算机中构成主从式并行环境就更为简单,只要在PC机上安装操作系统(本文安装linux操作系统)和MPI软件包就可以实现并行环境了。在共享内存多处理器计算机中,种群可以保存在共享内存中,每个处理器可以读取被分配到的个体信息并将适应度写回,不会有任何冲突。
4 实验结果分析
将以上方法实现的基于MPI的主从式遗传算法应用于1.2um SOI MOS器件的阈值电压模型参数提取工作中。如图4所示,实验结果表明曲线拟合的效果很好,转移特性曲线最大误差都低于5%。采用并行计算后,参数提取的速度提高了接近2.5倍。
5 结论
从实际的测试效果来看,以上方法实现的程序的简洁有效,智能化程度很高,且具有较高的精确度。因此,本文提出的基于MPI的主从式遗传算法可以解决遗传算法在器件参数提取过程中的耗时问题。该方法简单易用,适合推广使用。
参考文献
[1] J.Liou A,Analysis and Design of MOSFETS: Modeling,Simulation,and Parameter Extraction[M].KLUWER ACADEMIC PUBLISHERS,1998.
[2] Kondo M,Onodera H,Tamaru K.Model adaptable MOSFET parameter extraction method using an intermediate model[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,1998,17(5):400-405.
[3] Yang P, Chatterjee P K, An optimal parameter extraction program for MOSFET models[J].IEEE Transaction on Electron Devices,1983,30(9):1214-1219.
[4] Li Yiming. An automatic parameter extraction technique for advanced CMOS device modeling using genetic algorithm.Microelectronic Engineering,2006,41(4): 1309-1321.
[5] 康立山,非数值并行算法(第一册)-并行遗传算法[M].科学出版社,2003.
[6] 莱维尼,先进计算机体系结构与并行处理[M].电子工业出版社,2005.
