基于蚂蚁算法的PCB板路径优化研究

中北大学信息与通信工程学院 刘 鹏 姜 伟 刘新妹 殷俊龄

引言

在印刷电路板（PCB）焊接生产、故障检测以及维修过程中，现行以人工方式为主的路径规划方法缺乏严格的数学论证，特别在生产过程中由此制定的规划方案存在很大的随机性，经常发生自动化作业顺序不合理的情况，导致生产周期过长，影响整条生产线的生产。如何根据PCB板焊接的实际工作情况以及通用路径规划技术来寻求一种高效的路径规划解决方案，已成为PCB板制造业中的一个研究重点。

1.实际焊接生产过程分析

PCB板焊接过程中，必须先获得PCB板每一个焊点的确切位置和类型信息（以下统称为焊点信息）。获得焊点信息的方法有三种：

1）人机视角方式。这种方式的特点是设备附加成本低，易于实现。适用于印刷线路板上焊点数少或产品批量大的情况。但其效率较低，示教时有漏点的可能性，操作者劳动强度大。

2）图像处理方式。自动化程度高，能适用各种情况，但设备成本高、复杂及调研周期长。

3）从CAD文件提取方式。印刷线路板的制造目前已广泛采用计算机辅助设计方法。在印刷线路板的输出磁盘文件中已包含了各元器件及焊点的类型、位置等完整信息。

本文将采取从CAD文件提取焊点信息，通过逐点焊接的方式，控制系统驱动工作台移动，当待焊焊点到达激光斑点位置时工作台停止，系统按给定的加热功率及时间输出激光，此焊点焊接完成后，再移动到下一个焊点继续以相应的规范焊接，一直到所有焊点焊接完毕。显然当焊点的焊接规范给定后，全部焊接时间决定于总的行走路线。从焊接效率最高的角度分析，希望得到总的行走时间和行走路径最短的方案，但实现时费时巨大，首先要计算所有两焊点之间的距离，其次所有可能路径的计算也需要数目很大的加法运算，因此计算时间随着焊点数的增加而剧增。

2.优化方案的技术路线

在焊接PCB板工作过程中，焊枪从原始位置出发，途径各个焊点，最终回到原始位置，完成一个工作循环。这与TSP旅行商问题的数学模型非常类似，不同之处在于在PCB板焊接过程中还要考虑到焊枪和工件或夹具的干涉问题，这方面可以用增加虚焊点修正的方法加以解决。据此确定如下解决方案技术路线：

1）将问题转化成TSP旅行商问题的数学模型，并使用相应算法得到优化焊接顺序。

2）根据焊接工艺以及干涉等情况，加以修正。

3）最终确定合理焊接顺序。

3.优化算法论证

旅行商问题的一般描述为：旅行商从驻地出发，经过所有目的地一次后返回原地，应如何安排其旅行路线，才能使旅行距离最小。旅行商问题存在多种类型的求解算法，目前较为先进的多为仿生算法，其中包括穷蚁群算法、遗传算法和模拟退火法，神经网络法等。在此我们将分析目前最常用的3种算法：蚁群算法（ACS）、遗传算法（GA）和模拟退火法（SA）优化方法各自的特点，并对其收敛速度和优化精度进行论证对比。

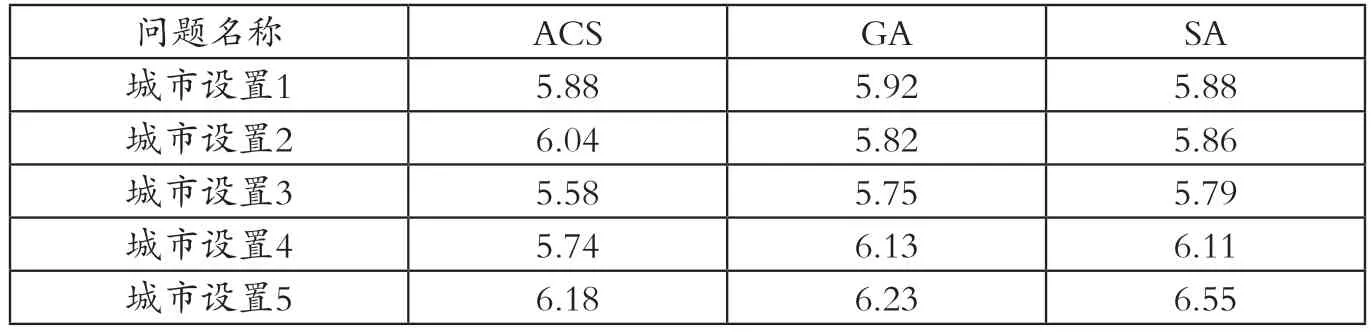
表1 3种算法在5组随机城市上的仿真结果[2]

表2 3种算法在3组几何问题上的仿真结果

图1 蚁群算法流程图

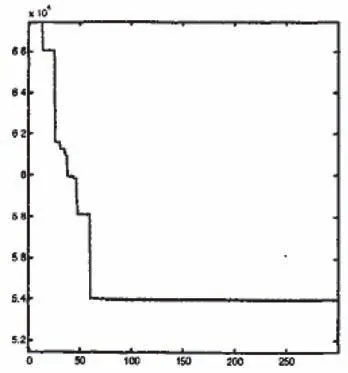
图2 收敛曲线

图3 路径优化结果

在这里采用蚁群系统作为蚁群算法的代表，与遗传算法以及模拟退火算法进行比较。考虑两组实验：第1组由5个随机产生的50个城市TSP问题组成；第2组包括3个在50和100个城市之间的几何问题。在这两组TSP测试问题上进行实验是很重要的，因为这两组问题具有结构上的不同，这使得它们对于一个算法实现起来很困难，而同时对于另一个算法却很简单，保证了对比的公平性。表l给出了在随机问题上运行的结果，黑体数字为已知最优解。

收敛速度是评价一个算法好坏的重要方面，因此我们对3种算法的收敛速度进行比较。从表2中可以看出，在同规模的测试问题上3种算法收敛到最优解的迭代次数相差很大。在Oliver30中，蚁群系统收敛到最优解是在第1470代，遗传算法是在第3200代，而模拟退火法是24617代。随着城市规模的增大，差距也随之增大。在Eil75中.蚁群系统收敛到最优解是在第4393代，遗传算法是在第80000代，而模拟退火法的收敛速度最慢，在第173250代才收敛到最优解。以上结果表明，蚁群算法的收敛速度最快。

以上两个的实验结果对比显示。ACS算法在求解节点数为5-100的组合优化问题上，选用合适的参数，其优化结果普遍好于遗传算法（GA）和模拟退火算法（SA）。

4.蚁群算法及技术方案的实现

蚁群算法的原理和计算流程如图1所示。

假设有n个待焊点，m只蚂蚁，τ（i,j）（i,j=1,2,…,n)表示顺序焊接的焊点i和j之间的残余信息量，初始时刻t（i,j)=c（c是常数)，蚂蚁k（k=1，2，…，m)在运动过程中根据信息量选择下一个要焊接的焊点，正在焊接的焊点r利用以下状态规则选择下一个要焊接的焊点S：

其中：allowed（k)表示蚂蚁k选择未焊接的焊点集合，η（I,j)表示t时刻焊接焊点i时选择焊点j为下一批焊接的焊点的启发函数，q为[0,1]的随机数，

q0∈（0,1)为实现变异的参数，β为参数表示启发函数，

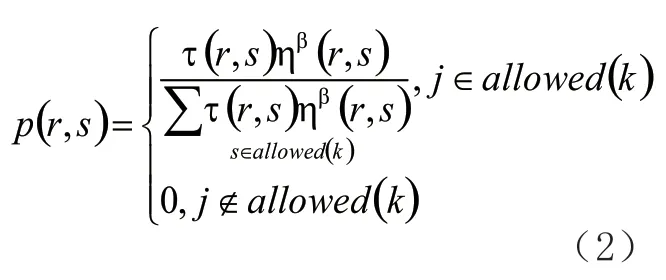
当每只蚂蚁都按状态规则确定了下一步要焊接的焊点，局部修改规则为：

其中：ρ∈（0,1)，

τ0=（Lmin*m)-1，Lmin为记录中的蚂蚁最小的完工时间。

当所有的蚂蚁全部运动结束后，记录当前循环中所有蚂蚁中的最小完工时间Lmin，全局修改规则为：τ（r,s)=（1-α)*τ（r,s)+α* L-1min

α∈（0,1）

根据上述流程在MATLAB中编写了相应的优化程序，将焊点坐标导入程序。选20个待测焊点路径顺序为[16 11 15 20 17 18 7 13 3 1 19 12 8 6 10 9 14 5 2 4]，所用时间为65.290162S，结果如图2、图3所示。

最后根据焊接工艺特点及具体情况进行适当的修正，获得最终结果。

结论

当蚁群算法用于PCB板的焊接路径优化时，蚂蚁之间通过一种简单的传递信息的方式—信息素来完成寻优工作。其核心问题是：1）选择机制：信息素越多的路径，被选中的概率越大；2）信息素更新机制：路径越短，迹增加越快；3）协作机制：个体之间通过信息素进行交流。

经过对PCB板的焊接路径优化，最终仿真结果比未优化的生产时间少15s，使得该PCB板工位的生产效率得以提高。同时也证明基于蚁群算法的PCB板路径规划方法是有效的。

[1]王涛,俞承芳.一种改进的粒子群算法在PCB板元件检测中的应用[J].微电子学与计算机,2007,24(12).

[2]李士勇,陈永强,李研.蚁群算法及其应用[M].哈尔滨:哈尔滨工业大学出版社,2004.

[3]王颖,谢剑英.一种自适应蚁群算法及其仿真研究[J].系统仿真学报,2002,14(1).