新型线性组合采样法SPWM谐波数值分析

严海龙 王榕生

（福州大学电气工程与自动化学院，福州 350108）

正弦脉宽调制SPWM[1-5]有不同的实现方法，通常有自然采样法、对称规则采样法及不对称规则采样法等。其中自然采样法涉及求解超越方程，一般只作为理论指导，而不对称规则采样法所形成的阶梯波较对称规则采样法更接近正弦波，因此实际应用中更多使用的是不对称规则采样法，但该方法采样次数比对称规则采样法多一倍，是以增大微处理器资源开销为代价获取波形的改善。即，不对称规则采样法存在着占用内存资源大的缺点。

本文针对上一问题提出了双顶点采样法，将之与对称规则采样法比较后，继而引出线性组合采样法。并重点采用Matlab软件编程对各种采样法SPWM作谐波数值分析。分析的结果表明一则双顶点采样法可以说是不实用的；二则线性组合采样法能够解决不对称规则采样法采样次数多、占处理器资源大的问题，而又不丢失不对称规则采样法谐波含量低的优点。

1 双顶点采样法SPWM

有没有什么方法可以有对称规则采样法一样的采样次数，但谐波含量能保持和不对称规则采样法相近的水平。比较容易想到的方法是两次采样分别在相邻的两个顶点（或底点）对称轴位置采样，在此称其为双顶点采样法，如图1所示。

双顶点采样法每个载波周期内的第二次采样都可以作为下一个周期的第一次采样，所以采样总数比不对称规则采样法少了一半，占用内存资源也随之少了一半，这一点达到了对称规则采样法的效果。由参考文献[3]可知，几种采样法脉宽计算公式分别是：

图1 双顶点采样法SPWM示意图

对称规则采样法：

利用Matlab强大的数值计算功能画出各种采样法SPWM波的理论波形，如图2所示。

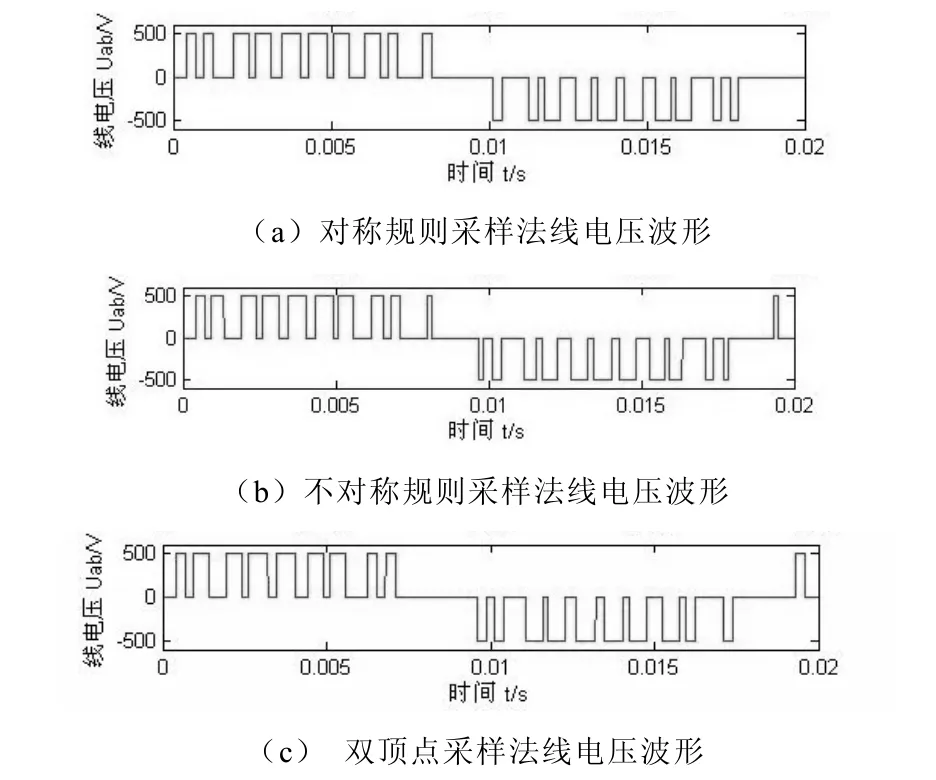
图2 规则采样与双顶点采样SPWM线电压波形

改变N（3的倍数），可以得到类似的波形，结果可以发现：对称规则采样法SPWM波形仅有1/2周波反对称，但无 1/4周波对称。而不对称规则采样法SPWM波形，在N取奇数时，波形兼有1/2周波反对称和1/4周波对称，在N取偶数时，只有1/4周波对称。总的来说，不对称规则采样法SPWM波比对称规则采样法SPWM波更逼近正弦波。还可以发现，双顶点采样法SPWM波形和对称规则采样法SPWM波形仅仅是前后倒置的关系。定量的分析可以从谐波计算入手，分别将上面3种采样法SPWM线电压傅里叶级数展开[4]，取不同的N值，都可以得到基本一致的结果（幅值大小不一样，但趋势一样），如图3所示。表明3种方法4N次（N为载波比）以下谐波中，含量比重较大的都是 2N± 、2 1N± 、3 2N± 、3 4N± 次谐波，即都是载波比及其倍数附近次数的谐波。

图3 规则采样与双顶点采样谐波幅值与次数的关系

单独对这些比重较大的谐波计算分析，发现随着M和N的变化，3种采样法的谐波幅值变化曲线是一致的[5]。另外，由于 2N± 、2 1N± 、3 2N± 、3 4N± 次谐波以及4N次以上的谐波次数都较高（实际应用中，N值都较大，平方之后更大），容易滤波，经输出滤波器以及电机漏感的抑制后，在负载端电压相应的畸变系数还是较小的，基于这两个原因，我们现可以只关心其余低次谐波的含量情况。在调制度M∈ [ 0,1]下，对低次谐波求总谐波失真系数THD，结果如图4和图5所示。

图4 规则采样线电压THD与M的关系

图5 双顶点采样线电压THD与M的关系

计算结果表明两点：①不对称规则采样法SPWM波谐波幅值较对称规则采样法小得多，②双顶点采样法 SPWM 波谐波幅值和对称规则采样法完全一致。

2 线性组合采样法SPWM

双顶点采样法没有保持不对称规则采样法谐波含量低的优点，但其为我们寻找新方法给以了一个提示，即利用相邻的两个顶点对称轴位置采样值的组合来得到类似于不对称规则采样法中底点位置的第二次采样值，得到线性组合采样法[5]，即第二次采样值等于相邻的两个顶点位置采样值的平均值。如图6所示。

图6 线性组合采样法SPWM示意图

采用线性组合采样法得到的 PWM 波形如图 7所示，可以发现，其与不对称规则采样法的已基本接近。定量的分析依然从谐波计算入手，发现载波比倍数附近次数的谐波和前面几种采样法一样，都是一致的。仍取其低次谐波THD值求解，计算结果如图8所示。可以发现，线性组合采样法线电压THD和不对称规则采样法THD在M较大时非常接近，随着M的减小，线性组合采样法在THD值方面会稍微更差些，但是这一差别会随着N的增大而迅速减小。实际变频调速应用中载波比N值（几百上千）都是远大于30的，这样THD值显然会和不对称规则采样法THD值更加逼近。

图7 线性组合采样法线电压波形

图8 线性组合采样线电压THD与M的关系

3 M文件关键程序段

利用Matlab编程计算分析以上几种采样法的波形及谐波，主要把握以下3点：①几种采样法SPWM虽然在电气意义上截然不同，但是如果单从数学和M程序上看，它们的区别仅仅在于sinwt2的不同；②由参考文献[3]可知，三相SPWM波脉宽计算公式在数学上的区别仅仅在于相差2π/3而已；③Matlab思维是数组式的处理，变量与自变量数组大小必须是一致的。以下是本次分析过程中的几条重要程序。

4 结论

（1）双顶点采样法 SPWM波和对称规则采样法比较，除了波形前后倒置外，谐波含量情况两者完全一致，也就是两者达到的SPWM波效果一致。但是前者算法较后者复杂，实时性较后者差，因此双顶点采样法是不实用的。

（2）线性组合采样法能克服不对称规则采样法采样次数多的缺点，而又不丢失不对称规则采样法谐波含量低的优点。

[1] BOWES S R, GREWAL S, HOLLIDAY D. High frequency PWM technique for two and three level single-phase inverters[J]. Electric Power Applications,IEEE Proceedings, 2000, 147(3): 181-191.

[2] BOWES S R, CLARK P R. Regular-sampled harmonicelimination PWM control of inverter drives[J]. IEEE Trans. on Power Electronics, 1995, 10(5):521-531.

[3] 王晓明.电动机的DSP控制——TI公司DSP应用[M].2版. 北京:北京航空航天大学出版社，2009：107-128.

[4] 陈坚．电力电子学——电力电子变换和控制技术[M].北京:高等教育出版社,2004:317-322.

[5] 王榕生．线性组合采样法SPWM新技术[J]. 电工电能新技术,2010,29(2):29-32.