数值模拟比值法计算水驱气藏体积波及系数

杨海，李闽，严东寅，王刚

（1.西南石油大学油气藏地质与开发工程国家重点实验室，四川 成都 610500；2.中国石油塔里木油田公司开发事业部，新疆 库尔勒 841000；3.中国石油新疆油田公司井下作业公司，新疆 克拉玛依 834000）

数值模拟比值法计算水驱气藏体积波及系数

杨海1，李闽1，严东寅2，王刚3

（1.西南石油大学油气藏地质与开发工程国家重点实验室，四川 成都 610500；2.中国石油塔里木油田公司开发事业部，新疆 库尔勒 841000；3.中国石油新疆油田公司井下作业公司，新疆 克拉玛依 834000）

水驱气藏体积波及系数不仅可以反映当前的水驱体积波及情况，而且在确定气藏最终采收率中有着重要的地位，同时也是判断气田开发状况和调整效果的重要参数。文中在考虑地层流体及孔隙体积影响的前提下推导出了被波及网格含气饱和度上限值R的计算公式，并利用数值模拟的方法通过判定水侵前后网格含气饱和度的比值与R的差值来确定气藏被波及网格数，从而计算水驱气藏体积波及系数。该方法消除了在生产过程中流体及固体状态的变化对网格气体饱和度所带来的影响，并引用数值模拟实例来说明比值法的应用。

数值模拟；体积波及系数；采收率；水驱气藏

油藏的水驱体积波及系数，定义为水驱开发条件下水侵占据的孔隙体积与油藏原始孔隙体积之比［1］。而水驱气藏，水驱体积波及系数的定义应为被水波及到的孔隙体积与原始含气孔隙体积之比。但是，目前而言，要直接通过现场分井分层测试资料计算水驱体积波及系数是很困难的［2-4］。

文中利用数值模拟技术，通过判定水侵前后网格含气饱和度的比值与被波及网格含气饱和度比值上限R的差值来确定被水波及网格数，进而确定水驱气藏体积波及系数。

1 基本公式推导

在气藏开发过程中随着地层压力的降低，地层流体会发生膨胀，岩石孔隙体积会降低，即释放其弹性能。这些释放的弹性能必将导致含气饱和度的变化。但是，仅由这些非水侵因素引起的含气饱和度变化的网格或孔隙不能视为被水体波及到的网格，所以在计算水侵前后含气饱和度变化时必须要扣除这样的网格。

地层原始条件下，含气饱和度［5］为

式中：Sgi为原始含气饱和度；Vg为地层原始条件下的地下含气体积，m3；Vp为孔隙体积，m3。

在生产过程中的某一时期，假设未受水侵影响，此时地层压力由原始压力pi降为p，则

气体的膨胀量为

地层水的膨胀量为

地层油的膨胀量为

式中：ΔVg，ΔVw，ΔVo分别为气体、地层水、地层油的膨胀量，m3；Bg，Bgi分别为地层压力p，pi时的气体体积系数，f；Vw，Vo分别为地层中水和油的原始地下体积，m3；Cw，Co分别为地层水、地层油的压缩系数，MPa-1；Δp为原始地层压力与当前地层压力的差值 （在实际网格计算时，Δp表示的是同一网格前后压力的差值），MPa。

若地层中含有油、气、水3相，则式（3）、式（4）可以分别改写为

式中：Swi为原始含油饱和度，f。

孔隙体积的变化量为

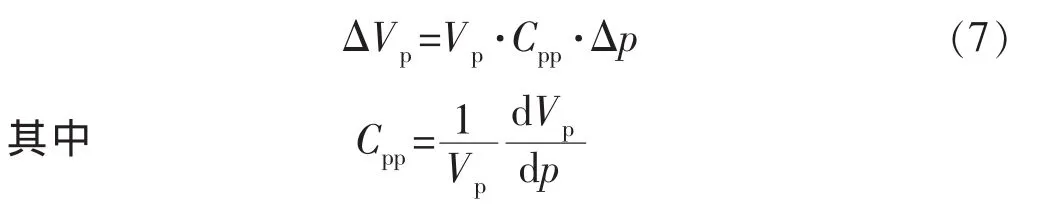
式中：Cpp为岩石孔隙压缩系数［6-7］，MPa-1。

由于上述流体膨胀的影响，当前地层压力p下孔隙的实际含气体积（地层含油、气、水3相）为

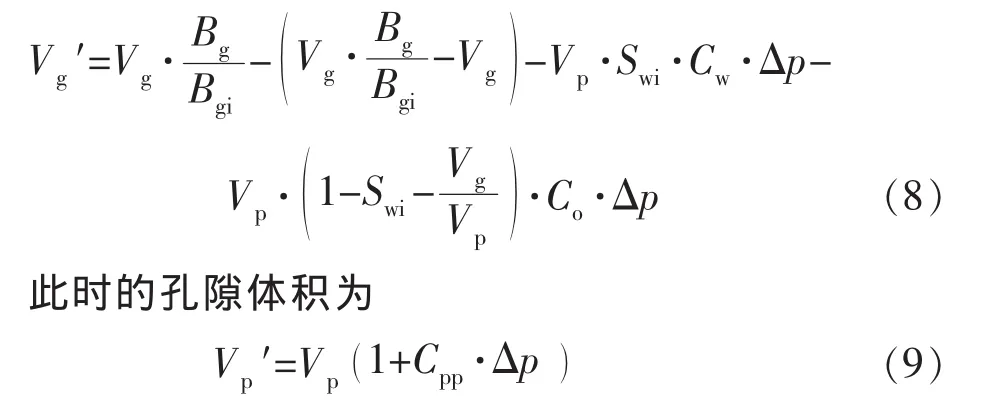
则当前地层压力p下含气饱和度（地层含油、气、水3相）为

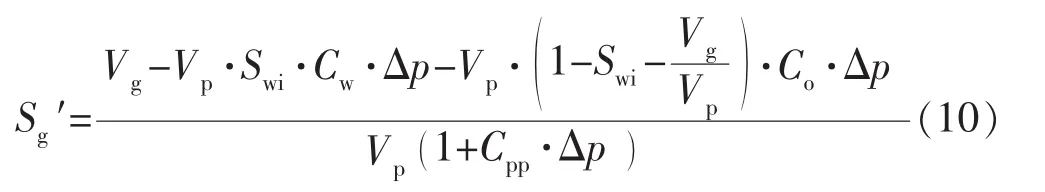
那么与原始含气饱和度的比值（地层含油、气、水3相）则为

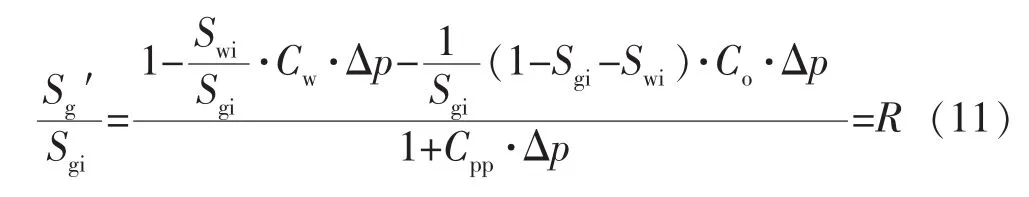
式中：R为计算所得到的比值，即被波及网格含气饱和度的比值上限。

地层只含气、水2相时，式（11）可以简化为

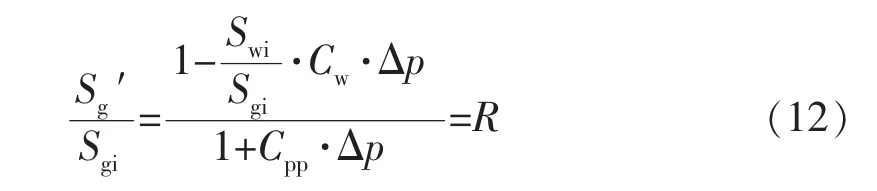
2 方法说明

利用数值模拟可以得出原始条件下每个网格的含气饱和度Sgi，含水饱和度Swi，以及所有模拟层位的含气网格数Ni，继而利用式（11）或式（12）可以求出每个网格对应的被波及网格含气饱和度比值上限R，同时可以得到某一生产时期，即某一地层压力条件下每个网格的含气饱和度Sg′。通过简单的编程可以计算出实际每个网格对应的Sg′/Sgi值，若其比值小于比值上限R则说明此网格含气饱和度的变化同时还受到水驱作用的影响，所以此时可视为此网格已被水侵。将所有这样的网格相加记为所有模拟层位的被波及网格数N2，则Ev=N2/Ni就是水驱气藏体积波及系数。

若在废弃压力条件下，则Sg′表示的是水驱气藏残余气饱和度Sgr，而N2/Ni表示的便是水驱气藏最终体积波及系数。其中的水驱气藏残余气饱和度亦可以由单向自发渗吸实验进行估算。

3 方法应用

文中采用Mxflu003模拟水驱气藏来说明饱和度比值法的应用，该模型只含气、水2相故将采用式（12）计算被波及网格含气饱和度上限值R。该模型网格类型采用笛卡尔坐标（28×32×6），网格数为5 376，有效网格数为4 093。

该气藏含有边底水，其水体厚度为30.48 m，半径为3 657.6 m，水体孔隙度为18%，渗透率为600×10-3μm2，水体密度为1.009 g/cm3，黏度为0.96 mPa·s，地层水压缩系数与岩石孔隙压缩系数均为4.348×10-4MPa-1。文中实例采用Carter-Tracy方法模拟水侵状况。生产时间从1996年1月1日到2000年12月31日（见图1—图4）。

图1 1996年1月1日含气饱和度分布示意

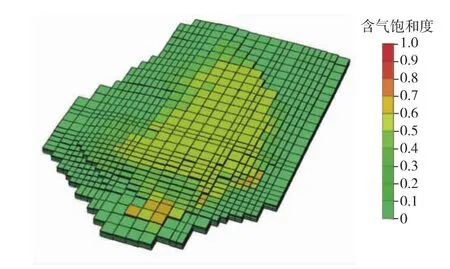
图2 2000年12月31日含气饱和度分布示意

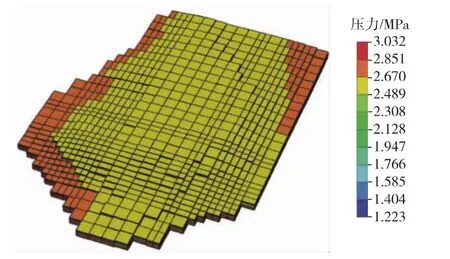
图3 1996年1月1日网格压力分布3D示意

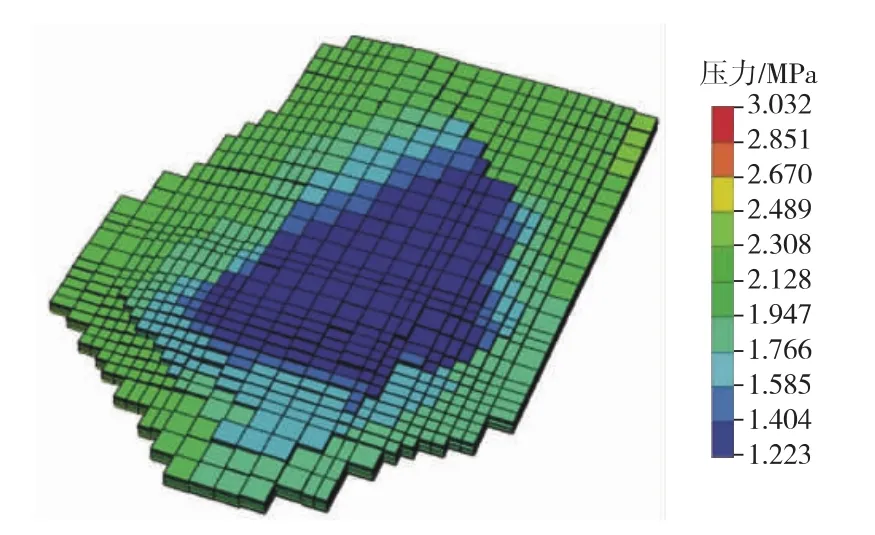
图4 2000年12月31日网格压力分布3D示意

将地层水压缩系数Cw、岩石孔隙压缩系数Cpp、各个网格的原始含气饱和度Sgi，以及原始与当前的压力差值Δp代入式（12），得出各个网格的被波及网格含气饱和度比值上限R。经编程计算得到模型中实际前后饱和度比值，小于对应的含气饱和度上限网格数N2为746，含原始气的网格数Ni为1 008，所以，截至2000年12月31日，该水驱气藏的体积波及系数Ev= 74.007 9%。

4 结论

1）水驱气藏体积波及系数即被波及网格数与含有原始气的网格数之比值。推导出了数值模拟比值法计算体积波及系数的理论公式。提供了一种计算水驱气藏体积波及系数有效简便的方法。若实际计算得到的网格前后饱和度比值小于本文中的被波及网格含气饱和度上限值R，则可认为此网格已被水波及。

2）用数值模拟方法在计算水驱气藏水体波及系数时，需要考虑地层流体，以及孔隙体积随压力的变化情况。计算波及网格数时，应将仅由于上述原因引起饱和度变化的网格予以扣除。

［1］陈元千.水驱体积波及系数变化关系的研究［J］.油气地质与采收率，2001，8（6）：49-51. Chen Yuanqian.A study on the changing relation of the water-flooding volumetric sweep factor［J］.Petroleum Geology and Recovery Efficiency，2001，8（6）：49-51.

［2］王任一.基于最大熵的岩心水驱波及系数求取方法［J］.断块油气田，2008，15（3）：91-93. Wang Renyi.A calculating method for water-flooding sweep efficiency of core based on maximal entropy［J］.Fault-Block Oil&Gas Field，2008，15（3）：91-93.

［3］黄郑，张建光，姚光庆，等.基于Welge方程的弹性水压驱动体积波及系数推导及应用［J］.断块油气田，2010，17（5）：586-588，592. Huang Zheng，Zhang Jianguang，Yao Guangqing，et al.Deduction and application of volumetric sweep efficiency for expansion water drive［J］.Fault-Block Oil&Gas Field，2010，17（5）：586-588，592.

［4］周炜，唐仲华，温静，等.应用数值模拟技术研究剩余油分布规律［J］.断块油气田，2010，17（3）：325-329. Zhou Wei，Tang Zhonghua，Wen Jing，et al.Study on distribution law of remaining oil by using reservoir numerical simulation technology［J］. Fault-Block Oil&Gas Field，2010，17（3）：325-329.

［5］何更生.油层物理［M］.北京：石油工业出版社，1994：11-28. He Gengsheng.Pertrophysics［M］.Beijing：Petroleum Industry Press，1994：11-28.

［6］Zimmerman R W.Compressibility of sandstones［M］.New York：Elsevier Science Publishing Company INC，1991：1-7.

［7］李海鹏，王道串，李蒋军，等.储层岩石压缩系数的一种预测方法［J］.断块油气田，2009，16（1）：45-47. Li Haipeng，Wang Daochuan，Li Jiangjun，et al.A prediction method for reservoir rock compressibility［J］.Fault-Block Oil&Gas Field，2009，16（1）：45-47.

（编辑 王淑玉）

Calculation of volumetric sweep efficiency for water-drive gas reservoir based on numerical simulation ratio method

Yang Hai1,Li Min1,Yan Dongyin2,Wang Gang3
(1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610500,China; 2.Development Department,Tarim Oilfield Company,PetroChina,Korla 841000,China;3.Downhole Operation Company,Xinjiang Oilfield Company,PetroChina,Karamay 834000,China)

The volumetric sweep efficiency of water-drive gas reservoir not only can reflect the current swept condition,but also can play a very important role in gas recovery calculation.Meanwhile,it can be applied to detect the production behaviors and check the stimulation operations.Considering the expansion of reservoir fluids and the decrease of pore volume,this paper derives the upperlimited value of gas saturation R of swept blocks,which is used to calculate the difference between R and the ratio of gas saturation before water influx to gas saturation after influx.The difference is applied to determine the number of swept blocks of water-drive gas reservoir by which the volumetric sweep efficiency can be obtained.It is viable to eliminate the influence on the gas saturation which caused by the change of fluids and rocks.This paper takes the numerical simulation example to introduce the application of the ratio method.

numerical simulation;volumetric sweep efficiency;recovery efficiency;water-drive gas reservoir

国家重点实验室国际合作项目“The Pressure Dependence of Permeability of Tight Reservoir Rocks”（PLN0901）资助

TE319；TE377

：A

1005-8907（2012）01-0103-03

2011-06-21；改回日期：2011-11-16。

杨海，男，1986年生，西南石油大学油气田开发工程在读硕士研究生。E-mail：sinoyh@126.com。

杨海，李闽，严东寅，等.数值模拟比值法计算水驱气藏体积波及系数［J］.断块油气田，2012，19（1）：103-105. Yang Hai，Li Min，Yan Dongyin，et al.Calculation of volumetric sweep efficiency for water-drive gas reservoir based on numerical simulation ratio method［J］.Fault-Block Oil&Gas Field，2012，19（1）：103-105.