关于卷积的运算规则及存在性
2012-04-26王晓翔梁忞飞
王晓翔,黄 静,梁忞飞
(合肥电子工程学院,安徽合肥 230037)
在“信号与系统”课程中,图解法是进行卷积运算的常用方法,然而在很多场合下直接用公式计算会更加便利,最关键的是积分上、下限的确定。我们发现,学生通常对时限信号和因果信号卷积较为熟悉,而对于其它情况下的卷积则不尽然,或者说没有概括性的了解。此外,关于卷积的存在问题书上也很少论及。本文对卷积在各种情况下的运算规则进行了归纳,并探讨了卷积的存在性以及它对卷积性质的影响,以期对学生更好地学习“信号与系统”课程提供帮助。
1 卷积的运算规则及存在性
1.1 常义函数卷积一定存在的情况
函数卷积的定义式为

两常义函数f1(t)与f2(t)满足以下两种情形之一时,卷积一定存在[1]:①两信号都是有始信号或有终信号或时限信号;②两信号中至少有一个是时限信号。
对于两时限信号卷积,教科书上均有详述,这里不再赘述。下面就其它几种情形的卷积运算规则进行归纳。
1)两有始信号卷积
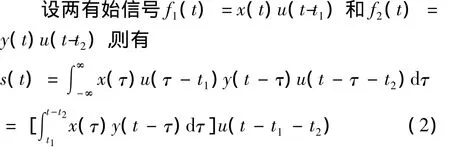


1.2 常义函数卷积不一定存在的情况
值得说明的是,前述文中提到的两常义函数卷积存在的条件(1)或(2)是充分条件而非必要条件。也就是说,当不满足这两个条件之一时,卷积可能存在也可能不存在。
两常义函数f1(t)与f2(t)满足以下情形之一时卷积不一定存在:①有始信号与有终信号;②有始信号与无时限信号;③有终信号与无时限信号;④两无时限信号。现就几种在假设卷积存在的运算规则进行归纳。
1)有始信号与有终信号卷积


上式成立的前提是每项的卷积都存在,此时各卷积计算可按前述方法进行。


2 卷积存在性对卷积性质的影响
2.1 卷积的分配律
卷积的分配律为

2.2 卷积的结合律
卷积的结合律为

该式成立的条件是f1(t)、f2(t)和f3(t)中的任意两者之间的卷积均存在[2],否则结合律不成立。如f1(t)=1,f2(t)=δ'(t),f3(t)=u(t),则有
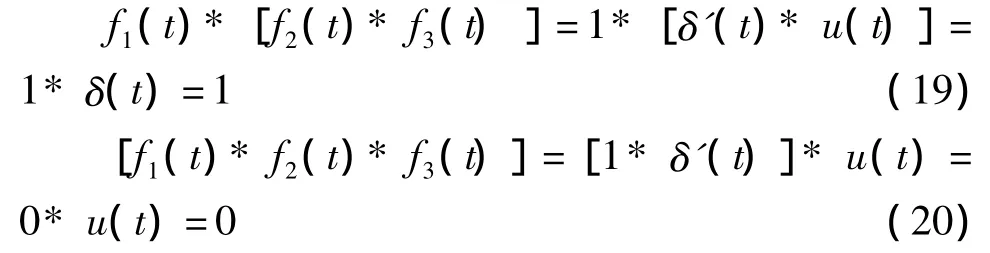
可见此时卷积的结合律不成立,究其原因是由于卷积f1(t)*f3(t)=1*u(t)不存在的缘故。
2.3 卷积的导数
卷积的导数是指

该式成立的条件是f1(t)*f2(t)存在。否则上式不成立。如卷积1*u(t)是不存在的,虽然卷积(1)'*u(t)=0和卷积1*u'(t)=1*δ(t)=1都存在,但是式(21)是不成立的。即:

2.4 卷积的积分
卷积的积分是指

该式成立的条件是f1(t)*f2(t)存在,而且有:[f1(t)*f2(t)]*u(t)满足结合律[3],否则上式不成立。如f1(t)=1,f2(t)= δ'(t),则有:[1* δ'(t)](-1)=0,[1](-1)* δ'(t)不存在,但是 1* [δ'(t)](-1)=1*δ(t)=1,可见此时卷积的积分式不成立,即有
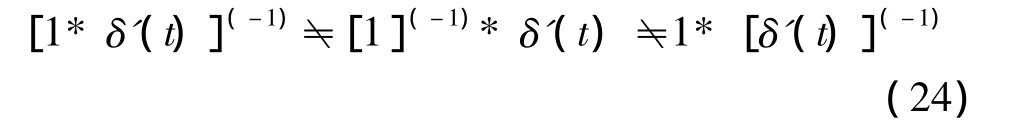
造成上述结果的原因是:虽然f1(t)*f2(t)=1*δ'(t)=0存在,但根据式(19)和式(20)可知:[f1(t)*f2(t)]*u(t)=[1* δ'(t)]*u(t)不满足结合律。
3 结语
本文对连续信号卷积的运算规则进行了归纳,事实上,得出的结论可以很方便地推广到离散信号卷积中去,只需将连续变量换成离散变量、积分换成求和即可。此外,关于广义函数卷积存在的条件,其详尽内容和证明可参见文献[3]。
卷积的分配律、结合律等是我们熟悉的卷积性质,然而它们成立的条件与卷积的存在性密切相关,盲目使用会产生错误的结果,这一点应引起重视。
[1]李化图.关于卷积及其存在性的探讨[J].重庆:邮电学院学报,1999(1):69-72
[2]王松林,王辉.“信号与系统”课程时域分析中的几个问题.[J].南京:电气电子教学学报,2008(6):16-17
[3]刘星桥.电工电子用广义函数.北京:电子工业出版社,2000
