应用分形两种迭代算法作短期负荷预测

张 巍 陈 恳

（南昌大学信息工程学院，南昌 330031）

负荷预测是供电部门的重要工作之一，准确的负荷预测，可以经济合理地安排电网内部发电机的起停，保持电网运行的安全稳定性，合理安排机组检修计划，保证社会的正常生产和生活，有效地降低发电成本，提高经济效益和社会效益。社会用电受很多相关因素的影响，例如政府的政策，国内国际政治，经济形势，昼夜以及季节和气候冷暖的影响，以及气温的变化，节假日，突发事故及电价等因素的影响。这些因素的存在都使得电力负荷的预测存在一定的随机性与不确定性，而分形能很好地解决复杂非线性问题。因此，本文运用分形拼贴原理以及分形插值算法建立预测模型，对短期电力负荷进行预测。本文还应用遗传算法探寻分形插值垂直比例因子，以实现分形插值曲线与实际函数曲线的拟合。

1 分形理论

分形理论是一门新兴的学科，其具有一定程度的应用普遍性。

1.1 分形拼贴定理

分形拼贴就是构造一个迭代函数系{X;W0,W1,…,Wn}，使得对给定集合L经此IFS变换后的结果拼贴成另一个集合A，两集合在Hausdorff距离下尽量接近。如果以电力负荷数据为给定的集合，那么存在一个迭代函数系{X;W0,W1,…,Wn}使得电力负荷历史数据集合在这组映射Wi（i=1,2,…,n）下的象趋近于电力负荷历史数据集合。

1.2 分形插值方法

分形插值方法[1-4]是对一组给定的信息点构造相应的迭代函数系IFS，使该IFS的吸引子为通过这组信息点的函数。给定一组数据{(xi,yi);i=1,2,…,n},要构造一个函数f(x)，使得给定的数据都经过f(x)绘制的图形或者趋近于函数图象，此f(x)就称为插值函数。

迭代函数系IFS(R2;wi,i=1,2,…,n)中每个函数wi的形式如下：

并且满足如下条件：

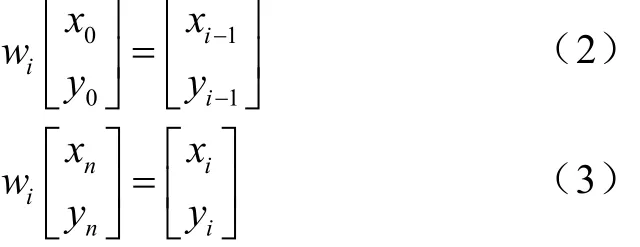
根据以上式（1）、（2）、（3）得以下方程组：

上式中，选定di为自由参数，即垂直尺度因子，则ai、ci、ei、fi可通过下式求得，即

确定了仿射变换的参数，就可以确定每个wi函数，接着利用分形迭代算法求取IFS的吸引子。

1.3 分形迭代算法

生成IFS吸引子的算法[5]有两种：

1）确定性迭代算法

（1）初始化，任意确定一个初始集，设定最大迭代步数。

（2）对这些初始集上的点依次进行各个iw变换，将变换后的点集保存。

（3）将步骤（2）中求得的每一个变换后的点集中的点都在屏幕上打出。

（4）返回第（2）步，直到迭代到最大步数为止。

2）随机迭代法

这是一种随机的选取IFS中仿射变换的方法。首先对每个仿射变换都附上一个概率ip，i=1,2,…，n，则IFS变成了含概率的IFS，形式为

随机迭代法的思想是：先在给定的数据中任取一个初始点x0，再随机地选取一个仿射变换wi，令x1=wi（x0）,…,如此下去，将得到一系列点的集合｛xn｝∞n=1，这些点构成的轨迹图即为分形图。其具体的算法步骤如下所示。

（1）设定一个初始点（x0,y0）及总的迭代次数。

（2）根据概率分布，以pi从仿射变换中随机选取一个wi。

（3）以wi作用初始点（x0,y0），得到新的点的坐标（x1,y1）。

（4）令x0=x1，y0=y1。

（5）在屏幕上打出点（x0,y0）。

（6）返回第二步，进行下一次迭代，直到迭代次数大于总的迭代次数。

由上述两种迭代算法的原理可知，两种迭代算法各有各的优点和缺点。确定性算法原理简单，能产生清晰完整的图像，但是占用了大量的内存空间，执行起来费时；而随机性算法是通过概率控制每次迭代IFS码被选中的次数，存储空间小，但随机性强，可能有IFS码在迭代过程中一直没被选中。

2 遗传算法对垂直比例因子寻优

迭代函数系各个参数除了由历史数据求取，垂直比例因子di也起着决定性的作用，所以如何选取di是非常重要的，因为它将影响分形曲线的起伏。本文利用遗传算法对di进行优化选取。针对电力负荷预测，本文对垂直比例因子寻优的算法过程如下

1）设定目标函数

本文用负荷预测的平均相对误差来定义遗传算法的目标函数：

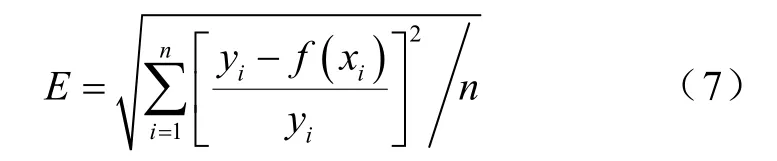
式中，f(xi)指的是分形插值曲线生成值，yi指的是给定的历史数据。选取di使上述适应度函数最小。

2）GA算法的具体步骤

（1）编码，利用二进制编码方式对垂直比例因子di进行编码。

（2）产生初始群体，随机产生初始群体，这第一代群体中的个体可能有id的最优解，但一般情况下没有，所以要对这些初始群体进行反复的交叉变异来寻求最优解。

（3）计算适应度，本文的适应度函数f=1/E，也即目标函数的倒数，确定了适应度函数，就对群体中的各个个体进行适应度的计算。

（4）选择，将各个个体的适应度按降序进行排列，从当代群体中选择优良的个体遗传到下一代。

（5）交叉，将优选后的个体以一定的交叉概率配对，形成新的群体。

（6）变异，将交叉后的新群体中的各个个体以一定的变异概率进行某个基因位或某些基因位上的基因值取反。

循环，产生新群体，对每一代的群体都进行反复的选择、交叉和变异，直到某一代群体中的所有个体的适应度函数都优于上一代群体。

3 分形理论在负荷预测中的应用

已经介绍了分形插值的方法及遗传算法对参数寻优的原理说明，下面就将这些原理方法具体应用到电力负荷预测中，步骤如下。

获取负荷样本，以四天的负荷为样本，选取三天为历史日，一天为预测日，三天的历史日中将邻近预测日的那一天定为基准日，其余两天为相似日。

先对基准日进行分形插值各个参数的求解，从基准日的96个负荷点中选取一定数量的特征点作为插值点，利用遗传算法对这些插值点进行初始群体的选取和编码，将二进制转为十进制，再代入1-5式进行各个参数的计算，继而利用确定性迭代算法和随机迭代算法得到基准日的分形曲线。再利用一般的插值方法求得各个插值点的负荷值，将这些值代入式（7）求取目标函数，接着可以得到第一代群体的各个适应度，然后根据GA算法中的选择、交叉和变异，以及一系列的循环优化，可以得到最后的id的最优解，将求得的垂直比例因子代入式（5）求取其余4个参数值，这样就得到了基准日的最优分形插值参数。

利用相同的求取基准日最优分形插值参数的方法来求得其他相似日的最优分形参数。

对求得的几个历史日的最优分形插值参数进行加权求均，得到一个统计意义上的分形插值参数，再利用确定性迭代算法和随机迭代算法分别进行吸引子的求取。该吸引子可以认为是预测日的分形插值曲线。

4 算例分析

本文根据南昌某地区的历史负荷数据来预测2011年11月12日的负荷，选取的历史日为11月的9、10、11日，11日为基准日，插值点选为：1，5，8，14，20，24，28，32，37，42，48，54，58，61，65，72，76，81，84，90，96共 21个点。利用分形插值理论以及遗传算法，得到了在两种分形迭代算法下的预测日负荷值，部分预测值见表1。

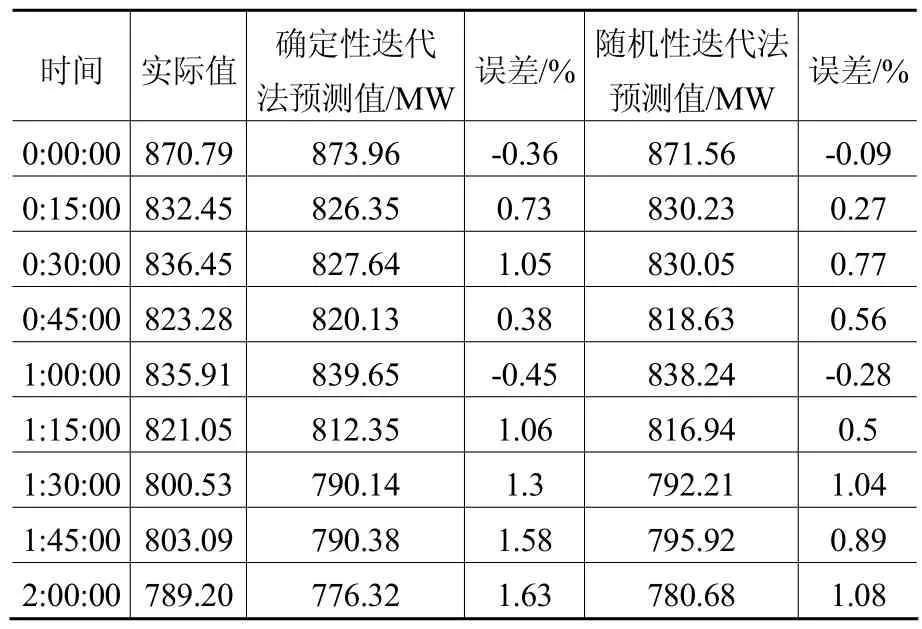
表1 预测日的部分预测值及其比较结果

表1中给出了预测日在两种分形迭代算法下的凌晨0点至2点间的负荷值及其误差，总体而言，应用随机性迭代算法比应用确定性迭代算法得到的预测结果更接近于电力负荷实际值。

由图1可以知道，两种分形迭代算法所作的负荷预测结果都与实际负荷值接近，但应用分形随机性迭代算法所得到的插值曲线与实际函数曲线的拟合度更高。

图1 两种迭代算法的预测负荷曲线与实际负荷值得比较

5 结论

本文应用分形插值理论以及分形迭代算法，再结合遗传算法对电力负荷进行预测，大大提高了预测的精度，特别是分形随机算法的应用，较之前常用的分形确定性算法在求取吸引子上有了很大程度上的精度的提高。然而本文也有很多需要改进的地方，比如没有考虑天气因素对负荷的影响，还有相似日权重系数的确定等。这些都对负荷预测的精度有一定程度的影响。

[1] 唐立春,李光熹,熊曼丽.基于分形的电力系统负荷预测[J].电力系统及其自动化学报,1999,11(4):21-24.

[2] RUAN H J，SHA ZH.Solving inverse problem of FIF by interpolating operator [J].Chinese J.Number.Math.And Appl.2000,22(3):1-11.

[3] DALLA L.Bivariate Fractal Interpolation Functions on Grids [J].Fractals,2002,10(1):53-58.

[4] CHATTERJEE M,LIN H T .Rate allocation and admission control for differentiated services in CDMA data networks[J].IEEE Transactions on Mobile Computing,2007,6(2):179-191.

[5] QI D X .Fractal and its computer generation[M].Beijing: Science press,1996: 67-69.