三支臂弧形闸门结构自振特性研究

谢智雄，梁明辉，胡霜天

(1.河海大学 机电工程学院，江苏 常州 213022;2.中国水电顾问集团北京勘测设计研究院，北京 100038)

0 引言

某水电站设12孔冲沙泄洪闸，孔口尺寸均为14 m×25 m(宽×高，下同)，工作闸门均采用三支臂弧形工作闸门，每孔1扇，共设置12扇，闸门高25 m，弧门半径为30 m，设计水头25 m，采用上悬挂式液压启闭机。对于这样的大型闸门，需要对其动力特性进行分析。闸门结构相关计算的传统方法多是将各部分作为平面问题进行计算，但不能反映结构部件的空间效应，实际上，三支臂弧形闸门为一空间板梁结构。本文运用ANSYS软件，按平面计算体系和空间结构体系分4种计算模式(杆件质量体系、支臂体系、主框架体系及空间结构体系)，对闸门结构的启闭杆、面板以及支臂3大结构部件的自振特性进行了分析计算，对不同模式下的计算结果进行了比较，从而较为全面地把握了闸门结构的自振特性。

1 计算模式

1.1 杆件质量体系

对于三支臂弧形闸门，可将启闭杆和支臂简化为杆件，将面板梁格结构简化为一个质量集中点。该体系有3种简化模式:

(1)杆系1:启闭杆和支臂简化为1个杆件，面板梁格结构简化为质量点放在支臂柱头上，如图1a所示。

(2)杆系2:支臂简化为3个杆件，面板梁格结构简化为质量点放在中间支臂柱头上，如图1b所示。

(3)杆系3:支臂简化为3个杆件，面板梁格结构简化为3个质量点，分别放在3个支臂柱头上，如图1c所示。

3种计算体系均在启闭杆上端与支铰处受到铰约束。

1.2 支臂体系

将支臂结构取出单独分析，按单个支臂(取1根支臂)和支臂架(取3个支臂)2种计算体系，分别按一端固定一端铰接和两端铰接2种边界约束条件进行计算，该体系又可分为4种计算模式:

(1)单个支臂1，两端铰接，如图2a所示。

(2)单个支臂2，一端铰接，一端固定，如图2b所示。

(3)支臂架体系1，支臂架两端铰接，如图2c所示。

图1 杆件质量体系

(4)支臂架体系2，支臂架一端铰接，一端固定，如图2d所示。

图2 支臂体系

1.3 主框架体系

主框架体系可分为平面框架体系和空间框架体系2种:

(1)平面框架体系:由2根支臂和1根主横梁构成一个平面结构，如图3a所示。

(2)空间框架体系:由闸门面板、支臂、主梁构成一个空间结构，如图3b所示。

主框架体系的边界约束条件均为支铰处受到铰约束。

1.4 空间整体结构体系

空间整体结构体系采用四节点板单元模拟闸门面板梁格及支臂结构，采用空间梁单元模拟支臂连接系，闸门结构的有限元模型如图4所示。计算时分2种情况:空间结构1和空间结构2。空间结构1不考虑附加水体作用，空间结构2考虑附加水体作用。

2 计算结果及分析

2.1 启闭杆及面板梁格沿切向的自振特性

不同计算模式下启闭杆及面板梁格沿切向的一阶自振频率计算结果见表1，从表1可以看出:

(1)启闭杆单独发生的横向弯曲振动，其频率在各种计算模式下相同，由此可见，启闭杆的自振频率不受计算模式和附加水体的影响。

(2)面板梁格沿切向振动的自振频率，3种杆系模式计算结果与空间结构1的结果分别相差17.7%，21.6%和13.6%。杆系3的计算结果比杆系1、杆系2的计算结果更接近空间结构的计算结果，但仍然存在一定差异。因此，可采用杆系3作为近似计算模型，若需精确结果还需要建立空间结构模型。

图3 主框架体系

图4 空间整体结构体系

表1 启闭杆及面板梁格沿切向的一阶自振频率 Hz

(3)面板梁格沿切向振动的自振频率，空间结构1和空间结构2的计算结果基本相同，这是由于附加水体质量仅沿闸门径向分布，水、固接触面只发生相对滑动。

2.2 支臂的自振特性

对于支臂振动，主要考虑其侧向振动和切向振动，而不考虑其径向振动。从单个支臂来看，侧向振动均以主框架平面内的振动为主，振型为一个或者几个正谐波，典型的振型图如图5所示;切向振动从单个支臂来看均以支臂架平面内的振动为主，振型为一个或者几个正谐波，典型的振型图如图6所示。各种计算模式下，支臂一阶振动频率见表2。

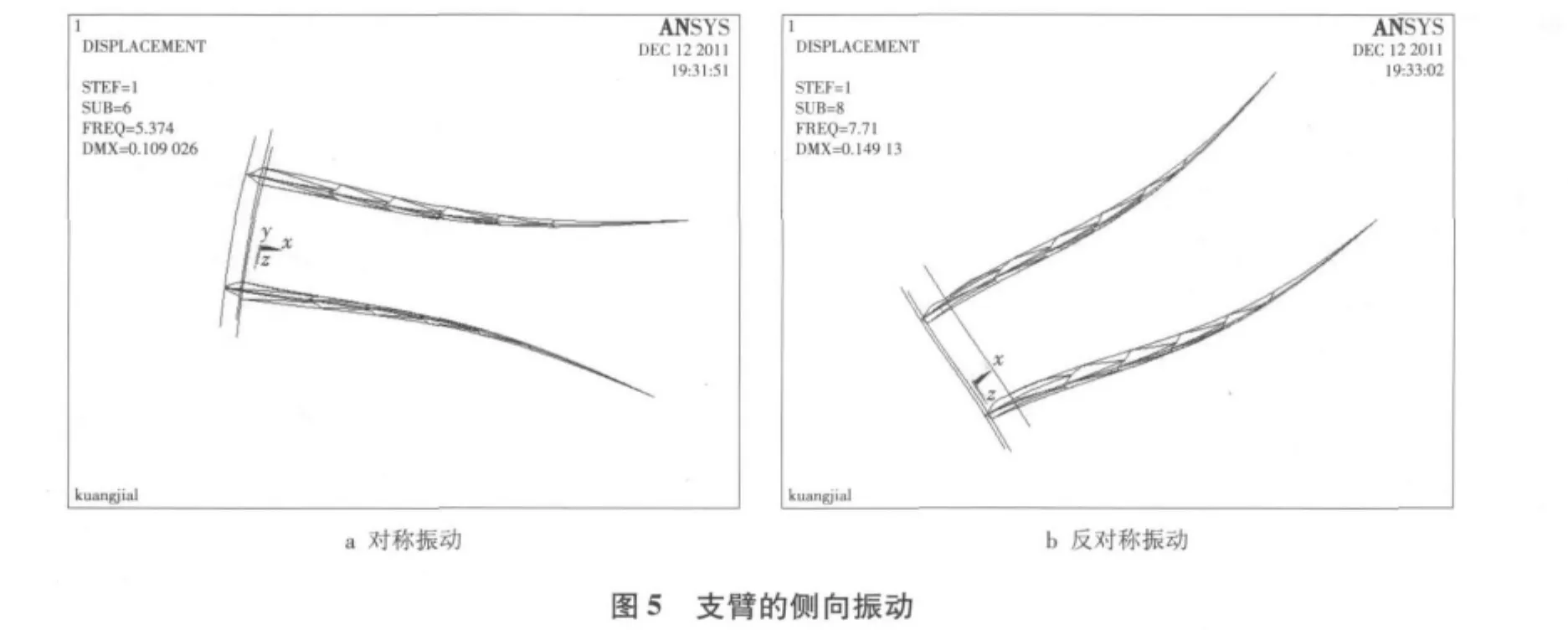
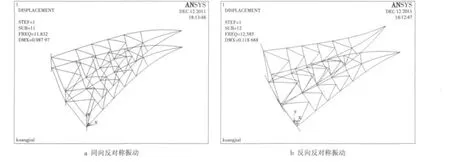
图6 支臂的切向振动

表2 支臂一阶自振频率Hz

2.2.1 支臂的侧向振动

表2中平面框架体系的数据对应于对称和反对称振动2种情况。

空间框架体系包括上、中、下3个平面框架体系，表2列出的数据对应以下振型:

(1)上、中、下主框架对称振动，振动方向相同。

(2)上、中、下主框架反对称振动，振动方向相同。

(3)上、下主框架对称振动，振动方向相反。

(4)上、下主框架反对称振动，振动方向相反。

(5)上、下主框架对称振动，方向相同;同时，中间主框架对称振动，方向与上、下主框架相反。

(6)上、下主框架反对称振动，方向相同;同时，中间主框架反对称振动，方向与上、下主框架相反。

空间结构的情况类同，由于出现板件局部振动后需进行计算的阶次过多，所以表2只列了较小的2个数值，对应于图5a、图5b 2种振动情况。

2.2.2 支臂的切向振动

表2中支臂架1和支臂架2的结果对应于反对称振动的情况。空间主框架结构包括左、右2个支臂架，因此产生了2种情况，表2中所列的空间主框架2个数值分别对应如下2种振动情况:

(1)左、右支臂架反对称振动，振动方向相同。

(2)左、右支臂架反对称振动，振动方向相反。

空间体系情况类同，由于考虑空间结构2附加水体左右需要计算的阶数过多，所以，表2中只列出了2个较小的数值，对应于图6a、图6b 2种振动情况。从表2的计算结果来看:

(1)按支臂计算时，其自振频率与其他计算模式相差较大，其原因在于没有考虑支臂间连接系的作用。

(2)按平面主框架体系计算时，一阶侧向自振频率与空间主框体系相差14.3%，与空间体系1相差6.3%。可见，计算支臂侧向振动时，可采用平面主框架体系作为近似计算模型。

(3)按支臂架体系计算时，支臂架1与支臂架2的一阶切向自振频率计算结果与空间主框体系分别相差6.2%和3.3%，与空间体系1分别相差8.8%和12.2%。

(4)按空间主框架体系计算时，与空间体系1相比，一阶侧向自振频率相差6.9%，一阶切向自振频率相差6.2%。可见，计算支臂切向振动时，可采用空间主框架体系作为近似计算模型。

(5)空间结构1与空间结构2相比，一阶侧向自振频率相差2.6%，一阶切向自振频率相差3.9%。

2.3 面板梁格沿径向的自振特性

闸门结构上部悬臂尺寸较大，因此，上部主横梁以上的悬臂端面板梁格首先振动，然后是中下部面板的整体振动，主要振型为对称振动和反对称振动。在空间结构体系下以及去掉支臂将面板梁格单独取出按不考虑附加水体作用时的面板梁格自振频率计算，结果见表3。从表3可以看出:

(1)面板梁格单独取出计算与空间结构1的计算结果比较，上、中、下3部分面板自振频率分别相差5.10%，0%和0.52%，结果基本一致，因此，可将面板梁格单独取出计算其沿径向的自振频率。

(2)考虑附加水体作用后，面板径向振动频率降低了37.2%～41.7%，这是由于附加水体质量只沿径向分布，只影响到面板梁格径向的振动，造成面板梁格径向振动频率大幅度降低;此外，在面板梁格各阶振动模态之间，还分布有较密集的面板区格局部振动频率带。

表3 面板梁格一阶径向振动频率 Hz

3 结论

本文将闸门结构分为启闭杆件、支臂和面板梁格3大部件，采取4种计算模式来计算闸门结构的自振频率并分析其振型，较为全面地把握了整个闸门结构的自振特性。通过对不同模式下计算结果的比较，可得出如下结论:

(1)启闭杆横向弯曲振动自振频率在各种计算模式下相同，可见，启闭杆的自振频率不受计算模式和附加水体的影响。

(2)面板梁格沿切向振动的自振频率，可采用杆系3作为近似计算模型。

(3)面板梁格沿径向振动的自振频率可将面板梁格单独作为近似计算模型来计算。

(4)由于支臂间连接系的作用，采用单个支臂体系计算模式计算的支臂侧向和切向振动结果与空间结构相比误差较大，不适合用作简化模型。

(5)计算支臂切向振动时，可采用空间主框架体系作为近似计算模型。

(6)计算支臂侧向振动时，可采用平面主框架体系作为近似计算模型。

以上计算若需精确结果还需要建立空间结构模型。

［1］谢智雄，周建方.大型弧形闸门静力特性有限元分析［J］.水利电力机械，2006，28(4):21－24.

［2］谢智雄，周建方.大型弧形闸门自振特性的计算［J］.河海大学常州分校学报，2006(3):25－28.

［3］水电站机电设计手册编写组.水电站机电设计手册:金属结构(一)［M］.北京:水利电力出版社，1988.

［4］DL/T 5013—1995，水利水电工程钢闸门设计规范［S］.