一种基于SLS_SVM的滚动轴承故障诊断方法

柴美娟，柳桂国

(浙江工商职业技术学院设备与设备管理办公室，浙江宁波 315012)

根据统计数据表明约有30%的滚动机械事故是由滚动轴承故障引发［1］，故作为滚动机械重要部件之一的滚动轴承，其性能直接影响着整个机械装置的性能，滚动轴承一旦发生故障，势必对整个机械造成损坏或停机，甚至造成人员伤亡事故，滚动轴承技术水平直接影响着机械行业的发展。目前，我国的滚动轴承行业发展迅速，市场需求不断扩大，但生产的滚动轴承大多为中低端产品，高质量产品主要依赖进口。滚动轴承行业这一现象的根本原因主要是缺少先进的检测和分析技术［2］。因此，对滚动轴承故障诊断方法进行研究具有一定的价值。

随着滚动轴承生产技术的发展，解析模型方法作为一种传统的滚动轴承故障诊断方法，已不适合解决越来越复杂的系统［3－4］。与其相比，以传统统计学为基础的基于数据学习的智能和信号处理方法，在处理复杂系统时表现出较大优势［5－6］，但其需要的样本数目较大。而在实际的滚动轴承故障诊断采的样本集往往有限。Vapnik V N于1995提出的支持向量机(Support Vector Machines，SVM［7］)是一种基于结构风险最小化准则的新统计学理论，该方法对小样本、非线性以及高维问题有较大优势。正是基于该算法的这一特点，李凌均在2002年将SVM应用于机械故障诊断中［8］，获得了较好的效果。在最小二乘支持向量机(LS_SVM)的基础上，万书亭教授于2009年提出基于LS_SVM的滚动轴承故障诊断方法［9］，并验证了该算法在保证了正确率的同时，还降低了计算复杂度，缩短了训练时间，该算法利用的是已知故障类型的有标签样本，属于监督式学习方法。

在实际的滚动轴承故障诊断应用中，大量统计样本的故障类型是未知的，即训练集中不单含有标签样本，同时还含有大量无标签样本。而同时利用有标签样本和无标签样本的半监督学习方法［10－11］，理论上可以弥补基于LS_SVM的滚动轴承故障诊断方法的不足。文中将半监督学习与LS_SVM相结合，给出一种基于LS_SVM的半监督学习滚动轴承故障诊断新方法(SLS_SVM)，该方法充分利用了训练集中的有标签样本和无标签样本所蕴含的信息，既具有LS_SVM的优点，缩短训练所需时间，也具有半监督学习的优点，利用无标签样本，改善分类器的正确率，在实际的滚动轴承故障诊断应用中，表现出有较好的性能。

1 最小二乘支持向量机(LS_SVM)

LS_SVM是将正则化理论应用于标准的SVM中的一种算法，该方法基本思想为:在标准SVM算法基础上，损失函数则采用LS线性系统，即优化指标采用平方项，提出数据中隐含的信息，并将SVM中的不等式约束转化为等式约束问题，故将二次规划的参数求解问题转变成解线性方程组问题，使计算复杂性降低，提高了计算速度，由于LS在求解不一致问题时，最小化误差平方之和，这就提高了 LS_SVM算法精度。

LS_SVM应用于滚动轴承故障诊断的两类分类算法描述过程如下:

预先统计出一个滚动轴承故障诊断训练集{(xi，yi)，i=1，2，…，N}，其中(xi，yi)为第 i个样本，yi∈{－1，+1}为一维输出类别，xi为n维输入训练向量，N为训练集中含有的样本数。LS_SVM算法的目标是确定一个超平面y(x)，将训练集分成两类:

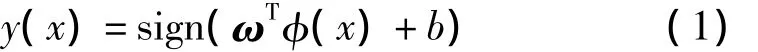
其中，当ωTφ(x)+b为正时，符号函数sign(·)为1，即y(x)=+1，反之为－1;ω为超平面法向量，b为超平面偏置常量，这两个参数都是待估计的未知参数。而非线性映射函数φ(x)将训练样本映射到高维特征空间，以线性不可分问题，即将原训练集映射到高维特征空间进行线性分类。

根据结构分先最小化原理，将其表示成一个等式约束优化问题，即可通过优化如下目标函数，获取LS_SVM的未知参数ω，b

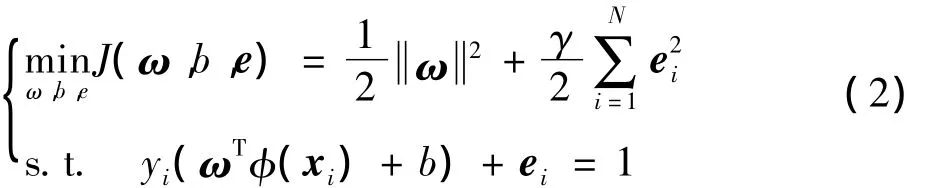
其中，ei∈RN×1为误差向量;γ≥0 为正则化参数。

为求解式(2)的优化问题，先将此约束优化问题转化为无约束优化问题，故引入 Lagr－ange多项式

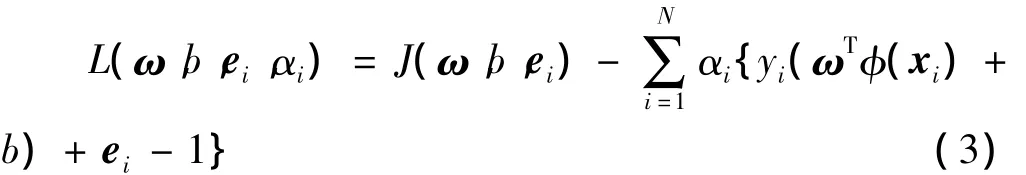
其中，αi是Lagrange乘子，在等式约束情况下，其值可为正或负。由KKT条件可知，上式优化条件为

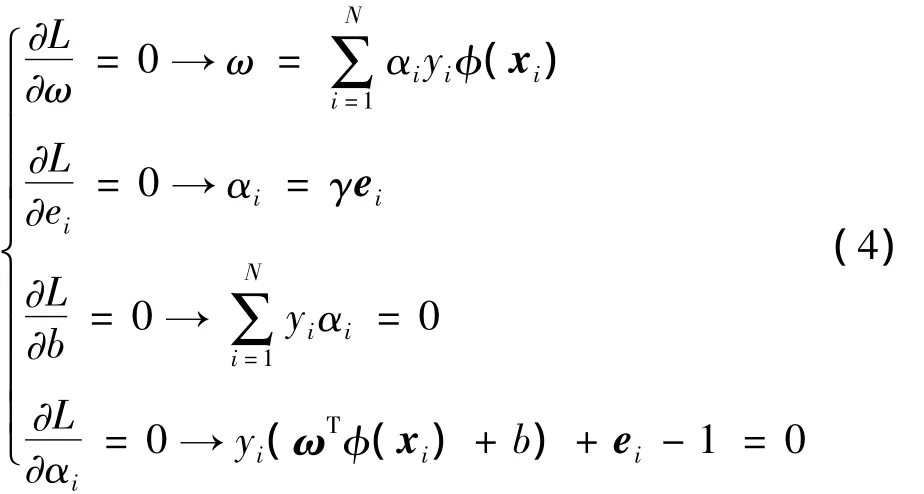
则上式可用如下线性方程组替代上式

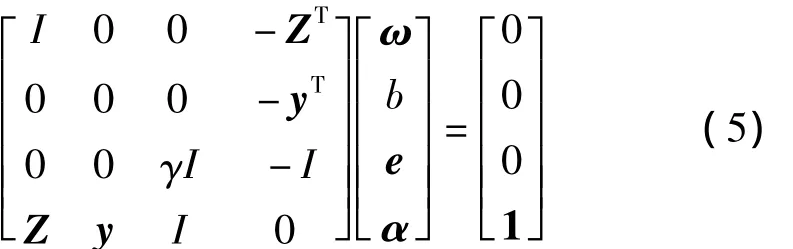
其中，Z=［yiφ(x1)，y2φ(x2)，…，yNφ(xN)］T，y=［y1，y2，…，yN］T，e=［e1，e2，…，eN］T，1=［1，1，…，1］T，α =［α1，α2，…，αN］T。

经过对上式进行消元，消除ei和ω后，在利用Mercer条件，最后形成如下矩阵形式

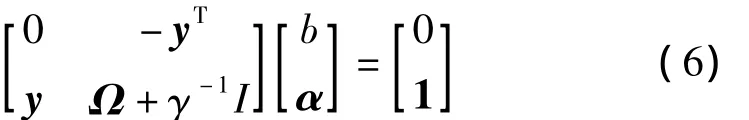
其中，Ω 中的元素 Ωij=yiyjφ(xi)Tφ(xj)=yiyjΨ(xi，xj)，再规定 A=Ω +γ－1I，故 A 为对称半正定矩阵，其逆矩阵 A－1存在，对线性方程组式(6)进行求解得

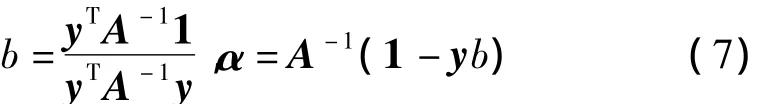
将式(7)中的α代入式(4)中的第一个等式，求出超平面法向量，并再将获得的ω和式(7)中的b一起代入式(1)中，则获得LS_SVM分类器的模型为

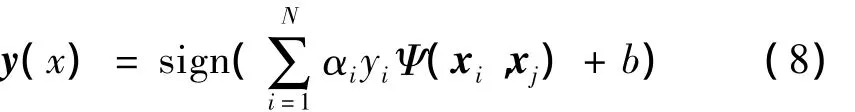
经过以上LS_SVM原理推导，不难发现，与SVM相比，其具有减小了计算复杂度以及提高了计算精度等优点。

但在实际的滚动轴承故障诊断应用中，在统计的故障训练集中，大量统计样本的故障类型是未知的，即训练集中不但含有标签样本，同时还含有大量无标签样本，此时的LS_SVM分类算法就会表现出其固有缺陷，由于该算法只能利用有标签样本训练出分类超平面进行分类，没有利用无标签样本，也就没有充分利用训练集中的有效信息。因此，可将半监督学习思想与LS_SVM原理进行结合，以充分利用滚动轴承故障诊断训练集中的有效信息，提高训练正确率。

2 基于SLS_SVM的滚动轴承故障诊断

标准的LS_SVM分类器利用人工分类好的样本来训练分类器，是一种有监督的学习方法，没有利用滚动轴承故障诊断训练集中的无标签样本。而半监督学习分类器则可以利用无标签样本，以改善分类器性能，因此，根据实际滚动轴承故障诊断的特点，探讨一种将LS_SVM与半监督学习相结合的分类方法，应用于实际的滚动轴承故障诊断中，具有重要的理论意义和应用价值。

1998年，Kristin率先利用混合整数规划思想，将SVM与半监督学习想结合，提出一种有效的分类方法［12］，并吸引了大量学者深入研究，随后提出了一系列改进分类算法［13－14］。而最早进行LS_SVM与半监督学习相结合的理论研究是张健沛教授，于2008年提出基于LS_SVM的半监督学习算法(SLS_SVM)［15］，并在理论上验证了该方法的巨大优势。但到目前为止，将基于SLS_SVM分类算法应用到实际中的研究还很少，且还没有文献将SLS_SVM分类算法应用与滚动轴承故障诊断之中。因此，在此根据滚动轴承故障诊断训练集特点，充分利用训练集样本信息，提出一种基于SLS_SVM的滚动轴承故障诊断方法，以改善分类器的训练正确率。

基于SLS_SVM的滚动轴承故障诊断方法的目的是在利用LS加快训练速度的同时，结合半监督学习，提高训练正确率。基本思想为:先利用滚动轴承故障诊断训练集中的有标签样本，用LS_SVM训练出一个原始分类器，再用该原始分类器对无标签样本进行分类，并进行相应的标注，在利用LS_SVM对新有标签样本进行标签动态更新。

在滚动轴承故障诊断中，诊断的可能结果有内环故障、外环故障、滚动体故障、其他故障、以及正常状态5类。在利用SL_SVM对训练集进行分类时，在此采用一对多分类方式，即训练样本具有M个类时，建立M个二值分类器，每一个类与其他类区别对待，也就是把当前类的输出定为1，而其他类的输出定为－1，所以，在对M类滚动轴承故障诊断时，需要建立M个分类器。一般情况下，可分5类滚动轴承故障诊断问题，故一对多滚动轴承故障诊断如图1所示。

图1 一对多滚动轴承故障诊断图

基于SLS_SVM的滚动轴承故障诊断方法的操作过程如下:

(1)提出故障诊断训练集的特征参数。

(2)利用LS_SVM对有标签样本进行一次训练，获取一个原始分类器y0。

(3)利用当前分类器对故障诊断训练集中的无标签样本进行分类，并进行相应赋值。对位于现在的超平面边界区域中的无标签样本进行区域标注。

(4)重置无标签故障诊断样本的标签。对所有样本进行再次训练，获取一个新的分类器y'，再用该分类器对无标签的故障诊断样本进行重新分类，并将此次无标签样本分类结果与上一次的分类结果进行对比，然后根据标签重置法则确定该样本的新标签。

(5)在当前边界区域内符合新加标签条件下，但还没有添加标签的无标签样本，使用区域标注法对其进行添加标签，并返回步骤(4)。若没有这样的无标签样本，就利用现在的分类器对剩余无标签样本进行分类，并添加标签。算法结束，并输出结果。

基于SLS_SVM的滚动轴承故障诊断方法，具有LS_SVN优点，同时，也具有半监督学习的优点，使滚动轴承故障诊断的训练时间得到缩短，也使训练正确率得到提高。

3 诊断试验结果并分析

为验证SLS－SVM在轴承故障诊断中的应用效果，将其与标准 SVM［7］、半监督 SVM［12］两种模型进行对比。并全部用以下6个特征参数，将特征参数L，C，K，M，CL，S，输入到最小二乘支持向量机多值分类器中，进行滚动轴承故障的模式识别。

实验选择3类不同的滚动轴承故障诊断训练集，从每一种轴承中选取25%作为有标签样本，另外75%作为无标签样本，分别在3种方法中进行独立实验，其实验结果如表1所示。

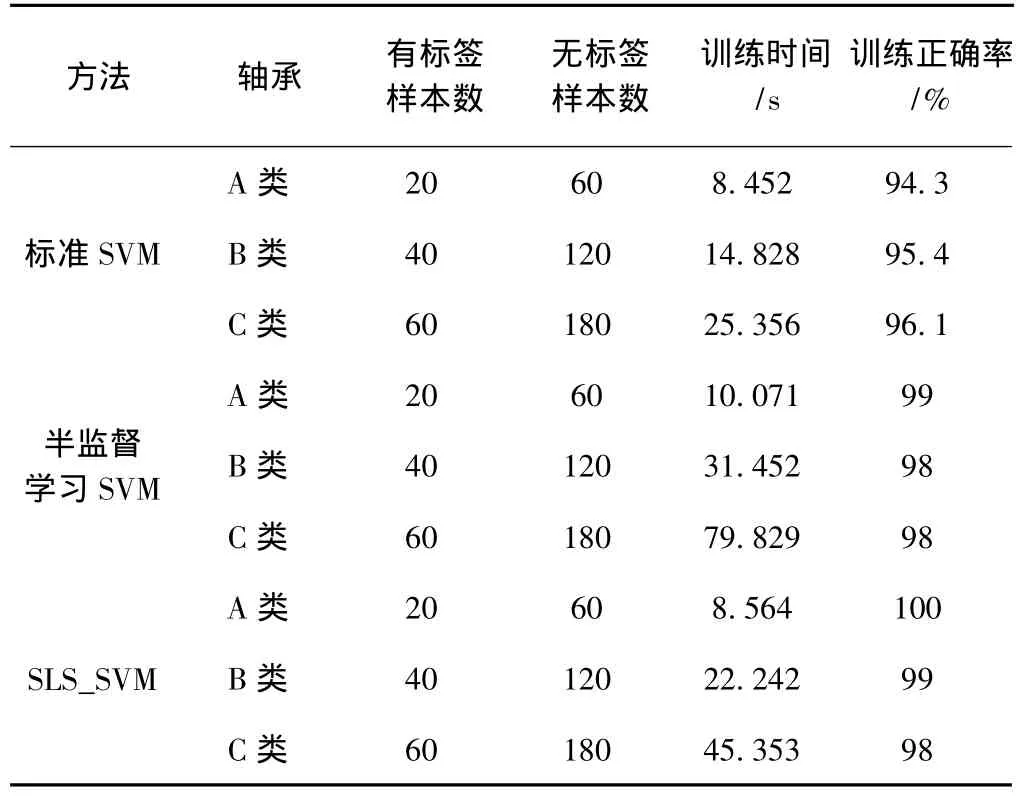
表1 本算法与传统算法的比较

分析表1中数据可知，在A类情况下，标准SVM、半监督学习SVM、以及文中的SLS_SVM所需时间分别为8.452 s、10.071 s和8.546 s，它们的训练正确率分别为94.3%、99%和100%，SLS_SVM相比没有利用最小二乘法的半监督学习SVM，缩短了时间。而在正确率方面，SLS_SVM相对于前两种算法分别提高了5.7%、1%，故该算法能提高训练正确率。同理，通过分析B类和C类情况下的训练时间和训练正确率，依然能得到以上结果，实验结果与理论相符。

与标准SVM和半监督学习SVM方法相比，SLS_SVM方法在滚动轴承故障诊断应用中，能提高训练的正确率，也能缩短训练所需时间，更适合实际工程应用。

4 结束语

在基于实际的滚动轴承故障诊断应用，针对统计的故障统训练集中，大量统计样本的故障类型是未知特点，给出一种新的基于SLS_SVM分类方法，该方法在利用LS_SVM对有标签样本进行处理的基础上，结合半监督学习思想，对大量无标签样本进行处理，以改进分类器性能。理论上阐明该方法的可行性，并通过滚动轴承故障诊断实验，验证了该算法的可行性，与标准SVM和半监督学习SVM方法相比，该方法能提高训练的正确率，也能缩短训练所需时间，具有较好的应用价值。

［1］ 梅宏斌.滚动轴承振动监测与诊断［M］.北京:机械工业出版社，1995.

［2］ 王雷，张华良，余光伟.滚动轴承故障只能诊断系统［J］.轴承，2006(8):31－33.

［3］ FRANK P M.Fault diagnosis in dynamic systems using analytical and knowledge－based redundancy a survey and some new results［J］.Automatic，1990，26(3):459 －474.

［4］ 彭涛.基于传感器最优配置的故障检测方法研究［D］.长沙:中南大学，2005.

［5］ PACHAUD C，SALVETAT R.Crest factor and kurtosis contributions to identify defects inducing periodical impulse forces［J］.Systems and Signal Processing，1997，11(6):903 －916.

［6］ PENG Tao，GUI Weihua，WU Min，et al.Fault diagnosis based on intelligent infor－mation processing technology［C］.Beijing:2002 IEEE Region 10 Conference on Computers，Communication，Control and Power Engineering，2002:1708－1712.

［7］ VAPNIK V N.The nature of statistical learning theory［M］.New York:Springer Verlag，1995.

［8］ 李凌均，张周锁，何正嘉.支持向量机在机械故障诊断中的应用研究［J］.计算机工程与应用，2002(19):19－21.

［9］ 万书亭，佟海侠，董炳辉.基于最小二乘支持向量机的滚动轴承故障诊断［J］.震动、测试与诊断，2009，30(2):149 －152.

［10］徐庆伶，汪西莉.一种基于支持向量机的半监督分类方法［J］.计算机技术与发展，2010，20(10):115 －121.

［11］夏士雄，李佑文，周勇.一种半监督局部线性嵌入算法的文本分类方法［J］.计算机应用研究，2010，27(1):64 －67.

［12］ KRISTIN P B，AYHAN D.Semi－ supervised support vector machines［C］.Cambridge:Proceedings of the 1998 Conference on Advances in Neural Information Processing Systems，MIT Press，1998:368 －374.

［13］ JOACHIM S T.Making large－scale SVM learning practical［C］.Cambridge:Advances in Kernel Method－Support Vector Learning，1999:169 －184.

［14］陈毅松，汪国平，董士梅.基于支持向量机的渐进直推式分类学习算法［J］.软件学报，2003，14(3):451 －460.

［15］张健沛，赵莹，杨静.最小二乘支持向量机的半监督学习算法［J］.哈尔滨工程大学学报，2008，29(10):1088－1092.