五点二重逼近细分法
2012-04-18庄兴龙檀结庆
庄兴龙, 檀结庆,
(1. 合肥工业大学数学学院,安徽 合肥 230009;2. 合肥工业大学计算机与信息学院,安徽 合肥 230009)
五点二重逼近细分法
庄兴龙1, 檀结庆1,2
(1. 合肥工业大学数学学院,安徽 合肥 230009;2. 合肥工业大学计算机与信息学院,安徽 合肥 230009)
提出了一种新的构造曲线的算法——五点二重逼近细分法。利用细分格式的生成多项式讨论了该细分格式的一致收敛性及Ck连续性。该细分格式带有一个张力参数μ, 通过选取不同的μ值,可以分别生成C1~C5连续的极限曲线。特别是当μ=9/256时, 细分格式生成的极限曲线可以达到 C7连续。最后给出了五点二重逼近曲线细分的实例,表明了这种细分格式是有效的。
二重逼近细分;生成多项式;Ck连续性;极限曲线
细分方法是基于网格细化的离散表示方法,是曲线曲面造型的一项重要技术。其基本思想是,给定初始控制网格,定义一个细分算法,在给定的初始网格中不断地插入新的顶点,使生成的网格序列收敛于一条光滑的曲线或一张光滑的曲面。由于其易在计算机上表示所以得到广泛的应用。Dyn等[1]利用三次Lagrange插值提出了一种四点二重逼近细分格式,其生成的极限曲线达到C2连续。Hassan等[2-3]第1次引入了三重细分格式的概念,并得到了三点三重逼近和四点三重插值细分算法。Siddiqi等[4]利用B样条基函数提出了一种能生成C4连续曲线的五点二重逼近细分算法(事实上,该算法只能生成C3连续的极限曲线)。Ko等[5]和Siddiqi等[6]将文献[1,4]的细分格式推广到三重的情形,分别得到四点三重逼近细分格式和五点三重逼近细分格式。Hormann等[7]从代数精度的角度出发,介绍了一种三点三重细分算法,其生成的细分曲线为 C1连续。Siddiqi等[8-9]引入了一个张力参数,分别得到改进的四点二重和改进的三点二重细分算法。郑红蝉等[10]介绍了双参数四点细分法及其性质。Daniel等[11]将细分格式推广到动态的情形,得到C2连续的三点二重动态细分格式。Dyn等[12]从理论上分析二重细分法及其极限曲线的收敛性和连续性。本文提出了一种构造细分曲线的五点二重逼近细分格式,并利用生成多项式等方法讨论了该算法生成的曲线的收敛性及 Ck连续性,得到光滑度更高的极限曲线。
1 预备知识
给定一系列初始控制点 P0= { p0∈ Rd},
i i∈Z设Pk= { pk∈ Rd}为第 k次细分后的控制点
i i∈Z集,则二重细分格式可表示为

其中, a = {ai}i∈Z为该细分格式的mask。
定理 1[12]若二重细分格式S一致收敛,则其mask a = {ai}i∈Z满足

定理 2[12]若二重细分格式 S 的 mask a = {ai}i∈Z满足式(2),则必存在一个二重细分格式 S1(称为S的一阶差分格式),满足

定理 3[10]若二重细分格式 S 的 mask a = {ai}i∈Z及其 j阶差分格式 Sj( j =1,2,… ,n)的满足


2 五点二重逼近细分格式及其收敛性和Ck连续性
首先给出五点二重逼近细分格式的定义。
定义1 已知初始控制点集为 P0= {pi0∈Rd},若 Pk= { pk∈ Rd}为第 k(k ≥0,
i∈Zi i∈Zk∈Z )次细分后的控制点集,则按下述递归定义第k+1次细分后的控制点

下面利用定理 2和定理 3讨论细分格式(3)的收敛性与 Ck连续性。
证明:由细分格式(3)可知该细分格式的生成多项式为

根据定理2可得1S的生成多项式为分格式(3)生成的极限曲线是2C 连续的。

则

从而根据定理 3可知,细分格式(3)生成的极限曲线是一致收敛的。
又由定理2可得2S的生成多项式为

则


证明:根据定理2可得3S的生成多项式为

则
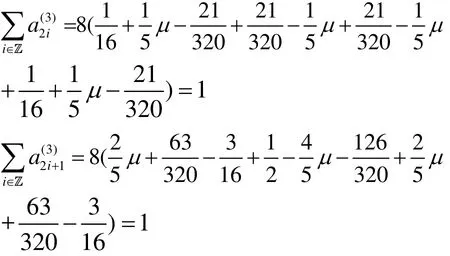

证明:根据定理 2可得4S的生成多项式为

则


证明:根据定理2可得 S5的生成多项式为

则


又6S的生成多项式为
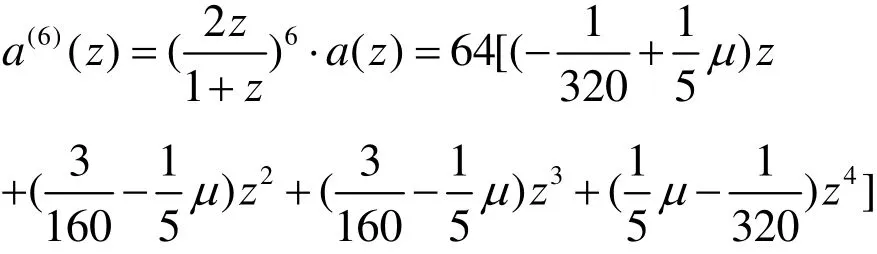
则


3 结论与数值算例
本文提出了一种构造极限曲线的五点二重逼近细分格式,并讨论了该细分格式的收敛性与Ck连续性。对于任意给定的初始控制多边形,可以通过选取不同的μ值得到一系列光滑程度不同的细分曲线。特别地,当 μ= 9/256时,细分格式生成的极限曲线是 C7连续的。 图1所示为在初始控制多边形给定的条件下,分别取μ=- 9/64,μ =- 13/128,μ =- 3/128,μ= 1/128时,基于本文的细分方法,经过5次细分,所得到的 C1,C2,C3,C5连续细分曲线,其中虚线和实线分别表示初始控制多边形与极限曲线。图2比较了在相同的初始控制多边形条件下,利用本文的细分方法与文献[1]、[4]、[6]的细分方法所得到的极限曲线,得出利用本文的方法生成的极限曲线具有更高的光滑度。

图1 五点二重逼近细分法算例

图2 本文的细分算法与其他几种细分算法的比较
[1] Dyn N, Floater M S, Hormann K. A C2four-point subdivision scheme with fourth order accuracy and its extensions [C]// Daehlen M, Mørken K, Schumaker L L(Eds.), Mathematical Methods for Curves and Surfaces: Tromso 2004, Nashboro Press, Brentwood, 2005: 145-156.
[2] Hassan M F, Dodgson N A. Ternary and three-point univariate subdivision schemes [C]//Cohen A, Merrien J L, Schumaker L L(Eds.), Curve and Surface Fitting: Saint-Malo 2002, Nashboro Press, Brentwood, 2003: 199-208.
[3] Hassan M F, Ivrissimitzis I P, Dodgson N A, et al. An interpolating 4-point C2ternary stationary subdivision scheme [J]. Computer Aided Geometric Design, 2002, 19: 1-18.
[4] Siddiqi S S, Ahmad N. A new five-point approximating subdivision scheme [J]. International Journal of Computer Mathematics, 2008, 85(1): 65-72.
[5] Ko K P, Lee B G, Yoon G J. A ternary 4-point approximating subdivision scheme [J]. Applied Mathematics and Computation, 2007, 190: 1563-1573.
[6] Siddiqi S S, Rehan K. A stationary ternary C4scheme for curve sketching [J]. European Journal of Scientific Research, 2009, 30(3): 380-388.
[7] Hormann K, SABIN M A. A family of subdivision schemes with cubic precision [J]. Computer Aided Geometric Design, 2008, 25: 41-52.
[8] Siddiqi S S, Rehan K. Improved binary four point subdivision scheme and new corner cutting scheme [J]. Computers and Mathematics with Applications, 2010, 59: 2647-2657.
[9] Siddiqi S S, Rehan K. Modified form of binary and ternary 3-point subdivision schemes [J]. Applied Mathematics and Computation, 2010, 216: 970- 982.
[10] 郑红蝉, 叶正麟, 赵红星. 双参数四点细分法及其性质[J]. 计算机辅助设计与图形学学报, 2004, 16(8): 1140-1145.
[11] Daniel S, Shunmugaraj P. An approximating C2non-stationary subdivision scheme [J]. Computer Aided Geometric Design, 2009, 26: 810-821.
[12] Dyn N. Subdivision schemes in CAGD [C]//Light W (Eds.), Advances in Numerical Analysis, Vol. 2, Oxford: Clarendon Press, 1992: 36-104.
A five-point binary approximating subdivision scheme for curve design
Zhuang Xinglong1, Tan Jieqing1,2
( 1. School of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China; 2. School of Computer & Information, Hefei University of Technology, Hefei Anhui 230009, China )
A binary five-point approximating subdivision scheme is described. The generating polynomial method is used to investigate the uniform convergence and Ck-continuity of this subdivision scheme. The subdivision scheme generates a family of Cn(n=1, 2,3,4,5) limiting curves for certain range of tension parameter μ and a C7limiting curves forμ=9/256. Some examples of the subdivision curve design are given to demonstrate the efficiency of the scheme.
binary approximating subdivision; generating polynomial; Ck-continuity; limiting curves
TP 391
A
2095-302X (2012)05-0057-05
2011-11-22;定稿日期:2011-12-09
国家自然科学基金资助项目(61070227,60773043);教育部科学技术研究重大资助项目(309017)
庄兴龙(1985-),男,福建福州人,硕士研究生,主要研究方向为计算机辅助几何设计。E-mail:zhuangxinglong@yeah.net
