贝叶斯网络推理分析的团树传播算法——以停车行为分析为例

李志瑶，宗 芳 ，张屹山b

(1.长春大学 机械工程学院，长春 130022;2.吉林大学 a.交通学院;b.商学院，长春 130021)

1 介绍

贝叶斯网络(Bayesian network)又称信度网络，是在多元统计分析技术中的贝叶斯决策方法的基础上发展起来的一种统计推断方法，于1988年由Pearl首次提出。它将概率论与图论相结合，能够系统地描述随机变量之间复杂的相关关系。贝叶斯网络一般由三部分组成:①结点集X和结点间的有向连接集A;②由结点集和有向连接集组成的有向连接图G;③每一个结点与其各父结点之间的条件概率组成的条件概率分布Θ。

近年来，贝叶斯网络以其独特的不确定性知识表达形式、丰富的概率表达能力、综合先验知识的增量学习特性，被广泛应用于辅助智能决策、模式识别、医疗诊断等领域。在交通领域，主要应用于交通行为分析、交通事故研究、短时交通量预测等方面。例如，鲜于建川、隽志才等(2011)应用改进的K2算法和贝叶斯参数估计方法构造通勤出行方式和出行链模式选择的局部贝叶斯网络［1］。宗芳等(2010)建立了停车行为分析的贝叶斯网络，并进行了停车收费等管理政策评价［2］。宗芳等(2011)运用相关性分析方法和K2算法建立了交通事故致因分析的贝叶斯网络［3］。梁俊秀(2010)基于贝叶斯网络的人的可靠性分析模型，对轨道交通系统司机的人因可靠性进行了定量分析，提出了基于Gibbs采样的交通贝叶斯网络近似概率推理算法，并进行交通流量的短时预测［4］。Janssens等(2006)结合应用决策树和贝叶斯网络描述人们的出行行为［5］。Hinsbergen等(2009)应用贝叶斯网络和神经网络预测出行时间［6］。但目前的研究主要注重贝叶斯网络参数估计和结构学习方法，对推理算法还没有足够重视。本文将研究贝叶斯网络的推理算法，并以停车行为分析的贝叶斯网络推理为例进行实例分析。

2 团树传播算法

贝叶斯网络推理是在给定一个贝叶斯网络模型的情况下，根据已知条件，利用贝叶斯概率中的条件概率计算方法，计算出所感兴趣的查询结点发生的概率。应用贝叶斯网络，可以根据网络中任意一个或多个结点的值推断其他结点的值。

贝叶斯网络推理有4种模式:①预测推理，由原因推(预测)结论，即已知一定的原因(证据)，用贝叶斯网络的推理计算，求出在该原因情况下结果发生的概率;②诊断推理，由结论推知原因，即已知结果，根据贝叶斯网络推理，找到造成该结果发生的原因和计算原因发生的概率;③原因关联推理，推理学习产生同一结果的不同原因之间的关系;④混合推理，上述几种推理模式的结合。该推理方法可用于求解网络中所有结点的概率分布。

现有的贝叶斯网络推理算法可分为精确推理算法和近似推理算法。精确推理算法适用于结构简单、网络规模小的贝叶斯网络推理。近似推理算法在不改变计算结果正确性的前提下降低了计算精度，从而简化计算复杂性，主要用于网络结构复杂、规模较大的贝叶斯网络推理。

团树传播算法是最常用的一种精确推理算法，其推理结果精确，计算效率较高。其主要思想是将贝叶斯网络转化为团树，然后通过定义在团树上的消息传递过程来进行概率计算，完成对网络的推理计算。其推理过程为:①确立推理函数;②在函数中添加证据函数;③向证据函数中输入证据结点的值，即添加证据;④输入想推理的结点编号或名称;⑤运行推理函数，得到在父结点影响下待分析结点的概率分布情况。

团树传播算法可以在Matlab通过engine=jtree_inf_engine(bnet)函数，调用联合树推理引擎来实现，并可以进行停车行为分析的贝叶斯网络的推理学习。基于团树传播算法的贝叶斯推理计算流程如图1所示。

图1 基于团树传播算法的贝叶斯推理计算流程

以下将以文献《基于贝叶斯网络的停车行为分析》所建的贝叶斯网络为例，详细说明团树传播算法的实现过程。图2为停车行为分析的贝叶斯网络结构图，表1为图中各变量的取值。

图2 停车行为分析的贝叶斯网络及其端正图

(1)构造端正图。将贝叶斯结构中每个结点的不同父结点结合，即在它们之间加一条边，然后去掉所有边的方向，所得到的无向图称为端正图。

表1 各影响变量的含义

(2)确定变量消元顺序。应用最大势搜索法确定变量消元顺序。设ξ是一个包含n个结点的端正图。最大势搜索对ξ中所有结点按如下规则从大到小进行编号:在第i步中，选择拥有最多已编号相邻结点的未编号结点，将其编号为n－i+1。如果这样的结点有多个，则任选其一。在所有的结点均被编号以后，按编号由小到大将结点排序，即得一个变量消元顺序。应用最大势搜索法确定停车行为分析的贝叶斯网络的变量消元顺序为 ＜sc，jf，f，j，l，s，g，m，k＞，确定消元顺序后的端正图如图3。

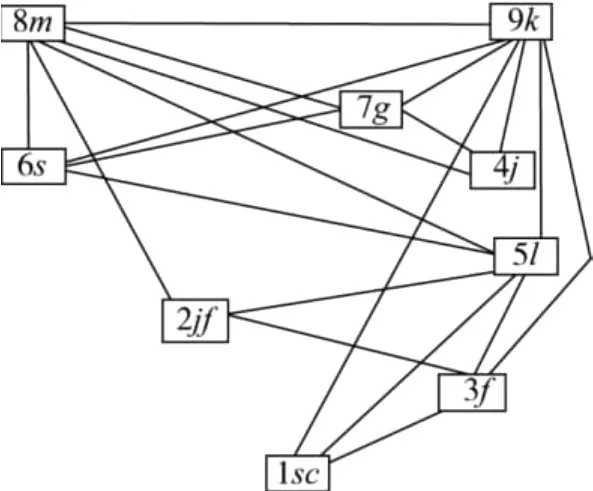
图3 应用最大势搜索法确定消元顺序后的端正图

(3)构造团树。构造团树的方法主要有图消元算法和BuildCT算法。其中，BuildCT(ξ，ρ)算法的基本思想是:从贝叶斯网G的端正图ξ出发，按一定顺序在ξ中进行变量消元;在消去变量X之前，先构造一个由X以及所有与X相邻的变量组成的团;在消元过程结束后，把所产生的团以适当方式进行组织，得到一棵覆盖G的团树ζ。应用BuildCT算法，所得团树如图4所示。

图4 停车行为分析的贝叶斯网络的团树

(4)设置推理证据。首先要确定推理中的证据变量，取值e。其后，设置推理中的查询变量，其集合为Q。根据查询变量的多少，推理过程可分为单查询变量推理和多查询变量推理，前者的查询变量仅有一个，而后者是在前者的基础上，利用团树的共享推理机制，简化计算过程后，推理得到多个查询变量的结果。

推理过程即为计算在证据变量的影响下查询变量的值的过程，即求解P(Q|E=e)。基本的计算公式为，

停车场类型和停车时长是两项重要的停车决策，将其设置为贝叶斯网络的查询变量，则所对应的推理为多查询变量推理。停车行为分析的贝叶斯网络的结点序列为［m］［g］［k］［s］［j］［l］［jf］［f］［sc］。其中，查询变量的集合Q=［l］［sc］，证据变量的集合evidence=［m］［g］［k］［s］［j］［jf］［f］。

根据文献［7］，团树传播算法(简记为CTP)的推理计算过程为:

输入:G－一个贝叶斯网;ζ－一棵覆盖G的团树;

E－证据变量;e－证据变量的取值;Q－一个查询变量。

输出:P(Q|E=e)

1:利用G将ζ初始化，即将G中的概率分布函数存储于ζ中的各结点处;

2:在ζ中的函数中，将证据变量E设置为其取值e;

3:在ζ中找出一个包含Q的团CQ作为枢纽;

4:for(每个与CQ相邻的结点C)

5:调用子程序CollectMessage1(ζ，CQ，C)获得一个函数;

6:end for

7:把上一步获得的函数以及储存在CQ处的函数相乘，得到C′Q的一个函数h(C′Q)，这里C′Q=CQE;

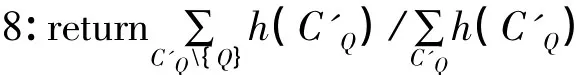
基于团树传播算法的多查询变量的贝叶斯推理算法将在调用子程序CollectMessage的基础上，引入另外两个子程序SaveMessage和RetrieveMessage，进行团树共享计算［7］。对于停车行为分析的贝叶斯网络推理，最终将通过单查询变量推理和多查询变量推理，计算并输出［l］［sc］两个查询变量的值。

3 停车行为推理分析

应用Matlab软件的jtree_inf_engine模块，停车行为分析的贝叶斯网络的推理结果介绍如下。

3.1 预测推理

假设已知某人因工作于非高峰时段开公车出行，想知道此人所选择停车场类型。证据为:

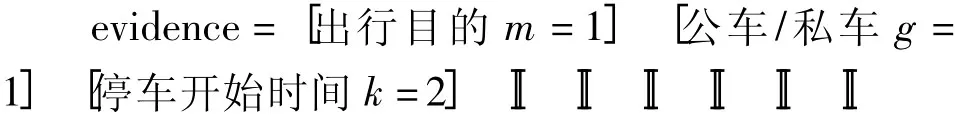
应用已建贝叶斯网络推理，得此人选择9个类型停车场的概率如表2所示。

表2 预测推理中某人选择各类型停车场的概率

分析表2中数据可知，此人选择居住小区停车场的可能性最大，其次是单位大院停车场。可以认为，如选择居住小区停车场，则此人的出行目的为工作出行中的回家;而如果选择单位大院停车场，则出行目的为工作出行中的上班或上学。

3.2 诊断推理

假设已知某人选择在2元/小时的停车场停放车辆5小时，想知道停车场类型和此人的出行目的。根据已建贝叶斯网络结构分析已知和待求各变量之间的推理顺序，知此问题为诊断推理方式。证据为:

应用已建贝叶斯网络推理，此人的出行目的分布如表3所示。

表3 诊断推理中某人的出行目的分布

分析表3中结果可知，此人的出行目的为生活出行的可能性大。应用已建贝叶斯网络推理，此人选择9个类型停车场的概率如表4所示。

表4 诊断推理中某人选择各类型停车场的概率

分析表4中结果可知，此人选择公建配建停车场的可能性最大，其次是路外停车场，这与停车时间和出行目的也比较相符。

3.3 原因关联推理

例如，在停车行为分析的贝叶斯网络中，停车场类型和停车费率是产生停车时长的直接原因。下面应用原因关联推理方法推理学习当停车时长为3小时及以下的短时停车时，停车场类型和停车费率之间的相互影响关系。证据为停车时长sc=1］。所得结果见表5。

表5 停车场类型与停车费率之间的关系

可见，停车场类型与停车费率之间的相关性较大。具体来说，占道停车(划线)、公建配建停车场收费较高，其次是立交桥下停车场、路外停车场、居住小区停车场，免费的停车场类型主要有临时路边、占道停车(未划线)、单位大院停车场和其他。这些推理分析结果与目前的停车管理现状吻合。

3.4 混合推理

假设已知某人开车购物，选择在2元/小时的停车场停放车辆5小时，则想知道此人开的车是公车还是私车，选择何种停车场。证据为:evidence==3］［停车时长sc=2］。

应用已建贝叶斯网络推理，得公车/私车的比例为0.1311:0.8689。可知，此人开私家车的概率大。停车场类型分布如表6所示。

表6 混合推理中某人选择各类型停车场的概率

分析结果可知，此人选择公建配建停车场的可能性最大，其次是路外停车场。与诊断推理案例相比，此例在新增出行目的为购物这样的证据下，选择公建配建停车场和路外停车场的概率有所增加。

4 结论

本文以贝叶斯网络的推理方法为主要研究内容，重点阐述了团树推理方法的基本过程和算法，以Matlab软件的engine=jtree_inf_engine(bnet)模块为主要工具，以停车行为分析的贝叶斯网络为例，进行了包括预测、诊断、原因关联和混合的全模式推理，并根据推理结果分析总结了居民的停车行为特征。研究结果表明，贝叶斯网络及团树推理方法可以应用于分析停车决策与停车者的个人属性、出行属性、停车属性等因素间的因果作用关系，以利于理解居民的停车决策特征。在此基础上还可以进一步诊断城市停车问题，提出和评价路内停车收费等管理政策的实施效果。

［1］鲜于建川，隽志才，朱泰英.基于贝叶斯网络的出行选择行为分析［J］.交通运输系统工程与信息，2011，11(5):167－172.

［2］宗芳，张慧永，隽志才.基于贝叶斯网络的停车行为分析［J］.系统工程理论实践，2010，30(5):948－954.

［3］许洪国，张慧永，宗芳.交通事故致因分析的贝叶斯网络建模［J］.吉林大学学报:工学版，2011，41(增刊1):89－94.

［4］梁俊秀.基于贝叶斯网络的轨道交通系统人因可靠性定量分析方法研究［D］.北京:北京交通大学，2010.

［5］Janssens D.，Wets G.，Brijs T.，Vanhoof K.，Arentze T.，Timmermans H.Integrating Bayesian networks and decision trees in a sequential rule-based transportation model［J］.European Journal of Operational Research，2006(175):16－34.

［6］Hinsbergen C.P.IJ.van，Lint J.W.C.van，Zuylen H.J.van.Bayesian committee of neural networks to predict travel times with confidence intervals［J］.Transportation Research Part C，2009(17):498－509.

［7］张连文，郭海鹏.贝叶斯网引论［M］.北京:科学出版社，2006.