曲率挠率的估计算法及其工艺嵌入

方丽菁， 卢卫君， 黄文钧

（广西民族大学数学与计算机科学学院，广西 南宁 530006）

曲率挠率的估计算法及其工艺嵌入

方丽菁， 卢卫君， 黄文钧

（广西民族大学数学与计算机科学学院，广西 南宁 530006）

几何处理和计算机视觉的很多应用依赖于几何性质，尤其是曲线的曲率和挠率。论文对非参数化的曲线提出了曲率和挠率的离散估计公式，以及消除噪音干扰的加权因子算法。还通过Maple程序，筛选统计出常见曲线的部分曲率和挠率参考值，提出理想曲率的大致范围和理想挠率的大致范围，并考虑嵌入到特定的工艺品中实验。

曲率估计算法；挠率估计算法；理想的曲率和挠率；工艺嵌入

曲线的几何性质是几何处理中着重采掘的特性，它们直接导致在机械视觉[1]和计算机图形学[2]的应用。在平面的情形，许多应用基于区域的曲率性质，比如曲线逼近[3]，几何压缩[2]，尤其是Attneave在早期文献后兴起的角点检测[4]。在三维空间情形，蕴含重要性质的曲率和挠率允许我们描述一条空间曲线如何弯曲和扭曲，因为曲率表征曲线在平面里的弯曲程度，而挠率表征曲线脱离既定平面的扭曲程度。曲率和挠率估计问题，一些学者已陆续提出些方法: Mokhatarian的高斯光滑法，通过挠率公式进行挠率估计[5]；Kehtarnavaz的B-样条技术[6]；Lewine的加权最小二乘拟合技术[2]；Raluben Medina提出的傅里叶变换法和最小二乘拟合法[7]，估计曲线上每一点的曲率值和挠率值。这些方法可应用于医学成像的动脉描述。文献[8]提出一种新颖的办法，基于空间曲线的局部几何参数化，将曲线分解成若干极大模糊片段的离散几何结论[9-11]扩充到 3D离散型的曲率和挠率估计量。本文给出了3D曲线的一种离散的曲率和挠率估值公式，并参考文献[2, 8]两种算法以达到精度要求和消除噪音。此外我们通过对现有常见的曲线，通过Maple程序，筛选统计出比较理想的曲率和挠率参考值及对应一些特殊曲率和挠率的曲线图库，提出理想曲率大致范围在 0.0～2.0之间，理想挠率大致范围在-0.5～0.5之间。我们尝试利用理想曲率和挠率范围绘制些带有特定曲率值或挠率值的近似曲线，希望嵌入到特定的工艺品中，以便对比实际效果。

1 曲线的曲率和挠率算法

正则曲线 r( t)的曲率和挠率有以下相应的计算公式[12-13]

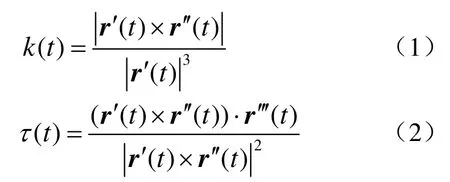
命题 1 对于未知参数表示的曲线C，在其上任取依次相邻的4个点 P1,P2,P3,P4。那么在点P2的近似曲率和在点 P3的近似挠率分别由下面式子给出

证明：设 P1T1, P2T2,P3T3分别是过点P1,P2和P3的切线，l(Pi,Pj)表示沿C从 Pi到 Pj的弧长。假设 l(P1,P2) = l(P2,P3)=Δs ，

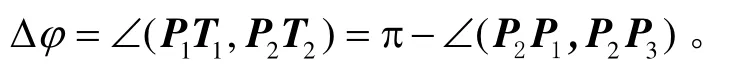
注意到 Δs→ 0时， Δϕ → 0，我们有

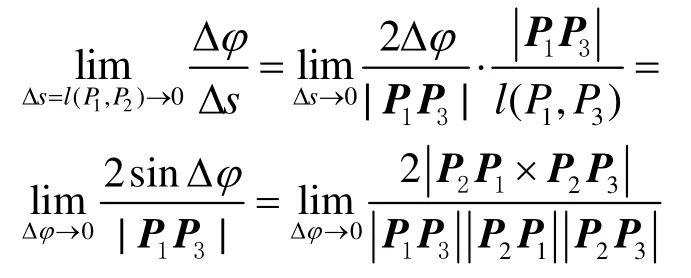
于是得到点 P2的曲率近似估计为（3）。

由于在 P3处的挠率表征了两个密切平面Δ P1P2P3和 Δ P2P3P4之间相对于弧段 P2P3的偏离程度，记 Δψ 为这两个密切平面的法向量P1P2×P2P3与 P2P3×P3P4的夹角，则有这样我们得到点 P3的挠率近似估计（4）。

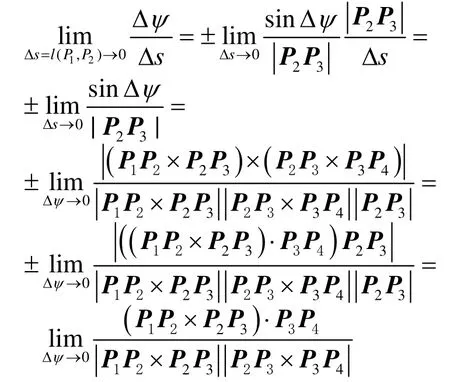
以上给出的算法也许比较粗糙，为达到一定的精度要求，我们可以通过多点估值加以平均化。

2 曲率和挠率加权估计算法[2,8]

对于空间轮廓曲线 r(t) =(x (t),y(t),z(t ))，假定它是至少 C3的正则曲线，但 x(t),y(t),z(t)并未已知。不妨假定 P0=r( 0)， P0与邻接的2q个点组成一个抗噪音区间 {P−q,P−q+1,…,P0,… ,Pq−1,Pq}。由于 r( t)在 t= 0处的Taylor展式为

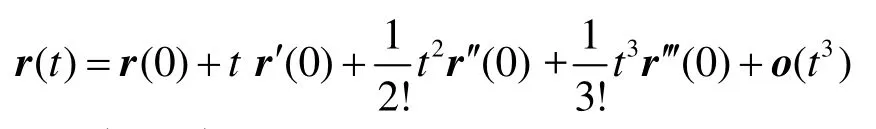
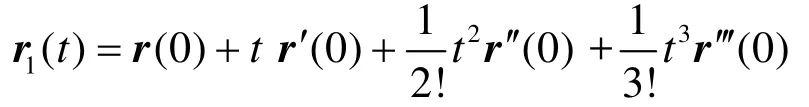
根据曲率公式（1）和挠率公式（2），只要求解出3个未知量r0′ =r′ (0),r0′ =r′ (0),r0′=r0′ ′(0)，就可计算出近似曲线r1(t)在 t= 0处的曲率 k1(0)和挠率τ1(0)，进一步可计算出原曲线 r( t)在 t= 0处的曲率 k (0)和挠率τ( 0)。容易验证 k (0) = k1(0)，τ( 0) = τ1(0)。有些文献为了计算方便，直接取在本文我们采用加权因子算法。

2.1 曲率加权估计的算法

首先考虑通过加权最小二乘法得到 r0′ = r′(P0), r0′ =r′ (P0)的估计，然后根据（1）及曲率不依赖坐标选取便得到曲率的估值。计算 r0′ ,r0′的分量x0′,x0′,y0′,y0′,z0′和 z0′，充分利用 P0点邻近的2 q+1个点 {P−q,P−q+1,… ,Pq}共同参与计算，以有效地消除了噪声干扰。

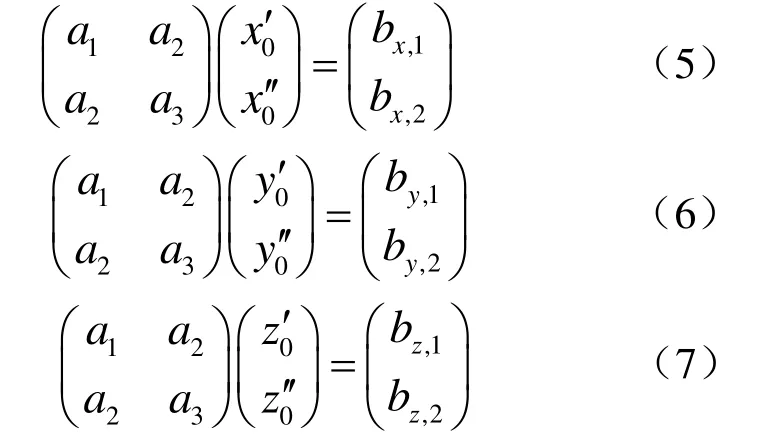
点 Pi的权重 wi必须是正数，且相对于(si为从点 P0到点 Pi的弧长)成反比例关系。例如，考虑加权因子的形式为 w= αexp(− β s2)/sk或简单

i ii取wi= 1。令 Δlk表示向量 PkPk+1的长度，k=−q,− q +1,… ,q ，则si可以由（ i＞0）和来估计。

其次，由式(5)～(7)得到 r( t)在 P0点的导数估计r0′,r0′，（1）给出曲率估计。

2.2 挠率加权估计的算法

假定P0=r( 0)，遵循文献[2]的方法，找出x0′,x0′和 x′(0 )使得x−分量加权方差函数

的逆矩阵解得，这里新的量

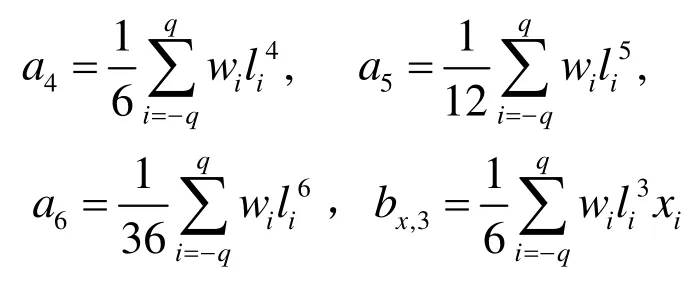
类似地，考虑 y0′ ,y0′ ,y0′和 z0′,z0′z0′分别对应的y−分量和z−分量加权最小二乘方程

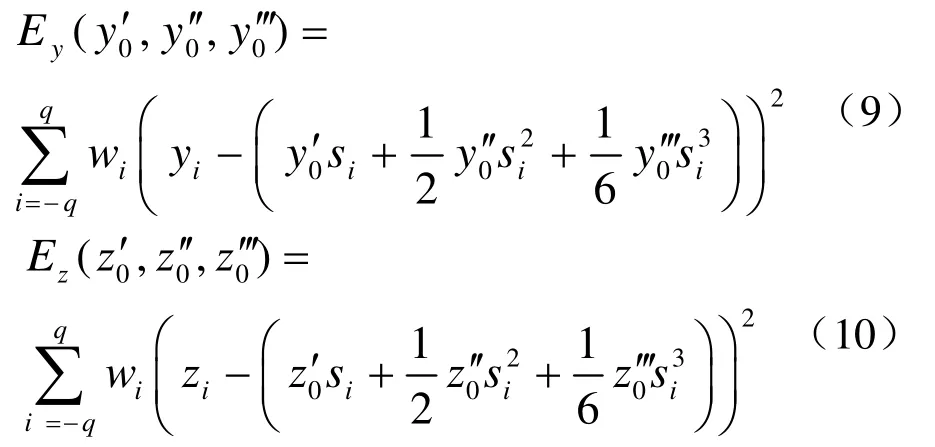
这样通过加权最小二乘方程组（8）～（10），得到 r( t)在 P0点的一阶、二阶和三阶导数估计r0′,r0′,r0′，（2）给出挠率估计。

血清HDL-C水平反映了遗传和环境因素间的相互作用，据研究报道，50%以上人类HDL-C水平的变异由遗传因素所引起［4］。DNA甲基化是一种可遗传性的、与心脑血管危险因素相关的可修饰的表观遗传标记，而且人类基因组约70%的CpG位点存在甲基化。脂质代谢的调控基因众多，本研究的目的是识别与血清脂质水平相关的DNA甲基化差异位点。本研究通过在新疆维吾尔族、哈萨克族、汉族自然人群中的研究发现，新疆维吾尔族、哈萨克族老年低高密度脂蛋白胆固醇血症可能与RANK基因甲基化率变异有关，RANK基因甲基化率增高可能是低高密度脂蛋白胆固醇血症的危险因素。

算法1实现挠率的估计，提供了估计曲率、挠率及3个基本向量的一种方法。知道了3个基本向量，我们便于以它们为新的坐标标架，画出近似曲线 r1(t)，具体见第4节。

Algorithm 1 Estimate torsion for space curves算法1 空间曲线的挠率估计1: call Set 3D Weighted Least Squares Variables; 2: call SOLVE■■■■■ ′′′■■■■■■■■■ ′ ′ ′■■■■■■■ ′ ′ ′■■= aaaxyz aaaxyz aaaxyz 124000 235000 456000■bbb bbb bbb■■■■xyz xyz xyz ,1 ,1 ,1 ,2 ,2 ,2 ,3 ,3 ,3■■3: k = r′ ×r′ r′ ; 3 4: r r r r r ; 5: τ =′×′⋅′ ′×′′() 2 T r r ; 6: ( ) =′′N r rTT; 7: =′− ′⋅N N N; 8: B = T ×N; =

3 由初始的曲率值和挠率值画出近似曲线

如果给定了某未知曲线的自然方程，即曲率函数和挠率函数，那么根据曲线论基本定理，我们通过Frenet公式得到这条曲线满足的常微分方程组

看作向量形式的 12个未知实函数，弧长s ∈ [a,b]，任意给定的初始值 r0,t0,n0,b0满足r( s)=r0, t( s) =t0, n (s0) =n0, b (s0)=b0且t0,n0,b0为右手系、单位正交。一般来说，这样的微分方程组的求解过程是比较困难，但有些时候即使不存在显式解，但其数值解也能产生一个解曲线。由于近十多年来计算机代数系统的发展，一般我们也可以做到这一点。比如运用Maple解给定曲率和挠率函数的微分方程组（11），其相关程序可参见文献[12]，可以得到相应的解析曲线，进而绘制出曲线。

现实中我们碰到且感兴趣问题，多数并不是给定一定区域内的曲率和挠率函数，而是随机或离散的输入特定的初始曲率值和挠率值，这样的曲线如何绘制出来？我们结合文献[13]相关思想整合出下面命题。

命题 2 给定两个数 κ0＞ 0,τ0，则存在一条空间三次曲线

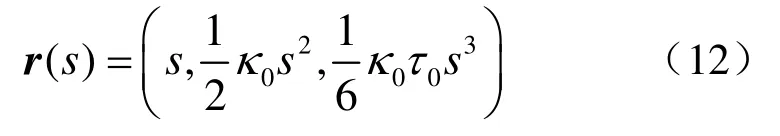
使得在参数 s= 0处它的曲率和挠率分为κ( 0)=κ0和τ ( 0)= τ0。

绘制给定曲率值和挠率值的局部近似曲线（12），我们可以先绘制它在 3个坐标平面的投影曲线图[13]，然后合成为空间 R3中的曲线。

4 理想的曲率和挠率的工艺嵌入

4.1 理想的曲率和挠率变动区间

对于一些常见的曲线，我们通过Maple程序（见[12]）计算下述一些特定曲线在某些特殊点的曲率和挠率

等。经过统计分析这些常见曲线的曲率挠率数据，得出曲线比较理想的曲率和挠率的取值范围：理想曲率大致范围在 0.0～2.0之间，理想挠率大致范围在-0.5～0.5之间。

这里所谓的理想是指几何外形的光滑和顺眼即美观问题[14]。比如按鼻子的美学标准，理想的鼻梁形态是在睁眼时重睑线的高度开始到鼻尖形成温柔的曲线轮廓（见图1）。理想的鼻尖曲率半径为8～12毫米，8毫米以下、12毫米以上均不理想，亦即鼻尖的理想曲率为0.0833～0.125之间。又如DNA超螺旋线的曲率挠率, 有人给出了两组曲率和挠率的特殊值(κ,τ)=(1.998,0.0132)和(κ,τ)= (7.9854,0.2139)[15]；还有人通过采样计算得到羊毛纤维形的平均曲率为 0.64mm−1，平均挠率为 0.09mm−1[16]。

至于这些数据的精度还有待进一步通过更多的曲率挠率数据库以及实验检验的反馈来修正。

图1 鼻梁轮廓线的美学对比

4.2 嵌入实例

我们的目标或想法，建立一定量的曲率和挠率大致理想的范围，以及它们相应的曲线段图像，根据工艺的特性和我们预备赋予的几何表现力，粘贴上带有特定的曲率挠率曲线加以改良。对于一些物件，如垃圾桶、装饰钟、瓶子、水龙头、TOTO小便斗、凳子、简易衣架等，考虑在某些局部上采用挖补匹配的手法嵌入这样具有理想的曲率和挠率的轮廓线，从而构建出新颖的曲挠造型。

我们想做几个实验：

实验 1 按曲率0.0833～0.125在指定的人脸上构建鼻梁，特别是鼻梁的轮廓线，变换几种模型，供矫正者选择。通过曲线方程（12）输入τ0= 0,κ0= 0.0833～0.125之间的几个数，容易得到所谓理想的鼻梁轮廓线（如图2）。

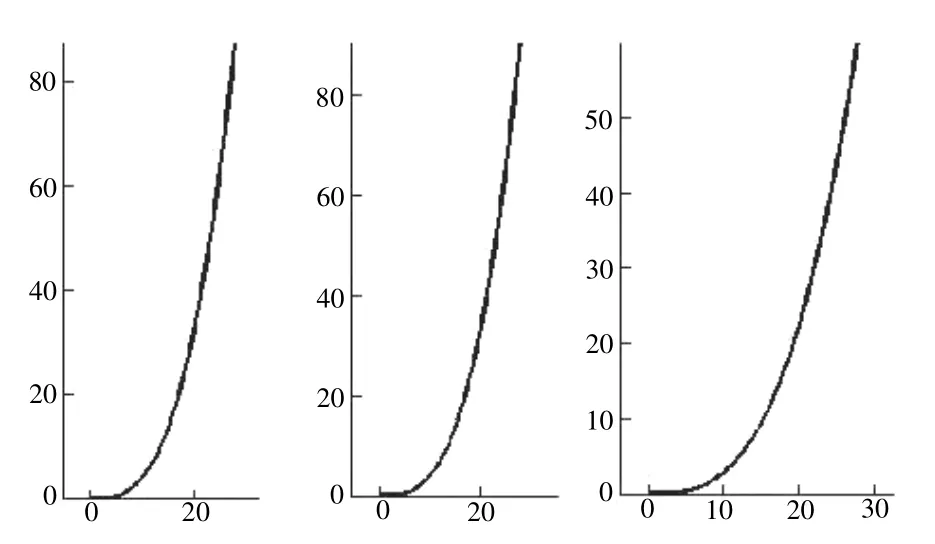
图2 带有理想曲率的鼻梁轮廓线

实验 2 输入 κ0在0.0～2.0之间的若干数值，及τ0取-0.5～0.5之间的数值，通过方程（12）看哪些局部生成的曲线跟下面的扭曲长椅图3吻合，嵌入特定点处的曲率和挠率值的片段曲线加工整合出新型的扭曲长椅, 这样的扭曲长椅置于户外，为陌生的人提供不同的空间，谁也不用碍着谁。

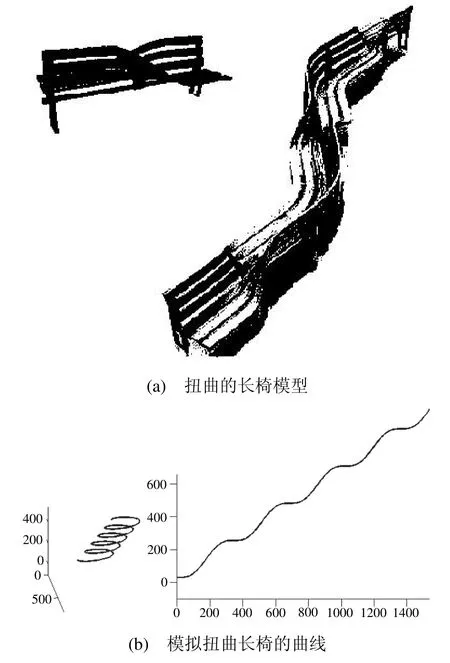
图3 扭曲的长椅

5 结论与展望

我们想开展的工作，建立曲率和挠率局部图库，结合带有加权的曲率挠率估计算法，通过近似曲线，实现在特定工艺的某些局部作嵌入曲率和挠率的手术，使其更加突出包装的性能，更富有观赏性。由于设备和技术上的问题，我们的嵌入实验还不是很成熟。此外，我们同样碰到纹理图像分割处理的困难[17]，如何将图像中属于同一种纹理的像素映射为相似的矢量，进一步将矢量映射为类别标号，实现从特征集合到分割结果的转化，局部上如何做些小手术嵌入我们希望的曲率和挠率。这些棘手的问题，我们正考虑采纳顾险峰和丘成桐等提出的纹理映射方法来探索[18]。

[1] Poyato A C, Garcıa N L F, Carnicer R M, et al. A method for dominant points detection and matching 2d object identification [C]//ICIAR, 2004, 1: 424-431.

[2] Lewiner T, Gomes J, Lopes H, et al. Curvature and torsion estimators based on parametric curve fitting [J]. Computers & Graphics, 2005, 29(5): 641-655.

[3] Salmon J P, Debled-Rennesson I, Wendling L. A new method to detect arcs and segments from curvature profiles [C]//ICPR , 2006, 3: 387-390.

[4] Attneave E. Some informational aspects of visual perception [J]. Psychol. Rev. 1954, 61(3): 183-193.

[5] Mokhtarian F. A theory of multiscale, torsion-based shape representation for space curves [J]. Computer Vision and Image Understanding, 1997, 68: 1–17.

[6] Kehtarnavaz N D, de Figueiredo R J P. A 3d contour segmentation scheme based on curvature and torsion [J]. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10: 707-713.

[7] Medina R, Wahle A, Olszewski M E, et al. Curvature and torsion estimation for coronary-artery motion analysis [C]// SPIE Medical Imaging, 2004, 5369: 504-515.

[8] Phuong Nguyen T, Rennesson I D. Curvature and torsion estimators for 3D curves [C]//Proceedings of ISVC, 2008, 1: 688-699.

[9] Debled-Rennesson I, Feschet F, Rouyer-Degli J. Optimal blurred segments decomposition of noisy shapes in linear time [J]. Computers & Graphics, 2006, 30(1): 30-36.

[10] Feschet F, Tougne L. Optimal time computation of the tangent of a discrete curve. Application to the curvature[C]//DGCI. 1999, 1568: 31-40.

[11] Coeurjolly D, Svensson S. Estimation of curvature along curves with application to fibres in 3d images of paper [C]//Scandinavian Conference on Image Analysis, Springer LNCS, Springer-Verlag LNCS. 2003, 2749: 247–254.

[12] John Oprea. Differential Geometry and Its Applications (Second Edition) [M]. Prentice Hall/Pearson, 2005: 1-36, 47-50.

[13] 陈维桓, 微分几何[M]. 北京: 北京大学出版社, 2006: 23-56.

[14] 王国瑾, 汪国昭, 郑建民. 计算机辅助几何设计[M].北京: 高等教育出版社, 海德堡: 施普林格出版社, 2001: 341-359.

[15] El Hassan M A, Calladine C R. Curvature and torsion of infinitely repeating DNA sequences: a geometric investigation [J]. Mathematical Physical and Engineering Sciences, 1997, 453(1957): 365-386.

[16] Marsh C, Tsang B, Wilkins A. Free wool-fibre shapes [J]. AUTEX Research Journal, 2003, 3(4): 153-159.

[17] 冯大淦. 基于特征的纹理图像分割技术研究[D].西安: 西北工业大学, 2006.

[18] Wang L, Gu X, Yau S T. Uniform texture synthesis and texture mapping using global parameterization [J]. The Visual Computer, 2005, 21(8-10): 801-810.

Estimate algorithms and embedded crafts of curvature and torsion

Fang Lijing, Lu Weijun, Huang Wenjun
( College of Mathematics and Computer Science, Guangxi University for Nationalities, Nanning Guangxi 530006, China )

Many applications of geometry processing and computer vision rely on geometric properties of curves, particularly their curvatures and torsions. This paper proposes some methods to estimate the curvature and the torsion, based on some algorithms for weighted least-squares fitting and local arc-length approximation in order to eliminate noises. By Maple procedure, statistical analysis of some selected common curves is carried out to get partial values of their curvatures and torsions, and then an approximate interval about ideal curvatures and ideal torsions is put forward. Furthermore, several test models for embedding specific ideal curvature or ideal torsion in crafts are taken into account.

curvature estimation algorithm; torsion estimation algorithm; ideal curvature and torsion; embedded craft

O 186.11; TP 391.72

2095-302X (2012)02-0009-05

2011-09-30

广西自然科学基金资助项目（桂科基0448019）

方丽菁（1960-），女，广西南宁人，副教授，主要研究方向为现代微分几何。