相依网络在不同攻击策略下的鲁棒性

刘润然， 贾春晓， 章剑林， 汪秉宏

（1.杭州师范大学阿里巴巴商学院，杭州 310036；2.中国科学技术大学物理学院，合肥 230026；3.上海理工大学复杂系统科学研究中心，上海 200093）

1 相依网络的鲁棒性研究进展

随着科学与技术的迅猛发展，各类基础设施之间的耦合和依赖变得越来越强烈，如城市的供水系统、电力系统、燃气系统、交通系统，以及通信系统之间都有着非常强的依赖关系［1－2］.具体的例子有：电力系统与通信系统之间的相互依赖关系，电力系统需要电信系统进行通信和调度，而通信系统又需要电力系统提供电力支持；类似的情况还有电力系统和铁路交通系统，铁路交通系统需要电力系统提供电力支持，而一些火电厂又需要铁路交通系统输送能源与物资.一个系统受到一点点的扰动，可能会触发其它系统的失效，进而又会影响到自身，从而会给整个社会带来灾难性的后果.例如，2003年9月23日的意大利大停电事件，就是由一个电力站的失效导致很多电力节点与整个电网的脱离，接着又导致很多互联网节点的失效，最终导致调度系统无法对整个电力网络进行有效的调控，从而诱发了更大规模的电力节点的失效［1］.另外一个国内实例是在2008年春季，中国南方的雪灾导致电力网络的失效，从而诱发了铁路交通网络的不畅，而铁路运输的不畅又导致了部分电厂无法得到能源的补给，从而使电力系统和铁路交通系统都难以恢复畅通，最终给华南的广大地区带来了非常严重的灾害.因此，对这类相依系统鲁棒性的研究有着非常强的现实意义［1－5］.

复杂网络是研究复杂系统的有力工具之一，研究复杂网络的鲁棒性不但对于理解复杂系统的组织形式与功能之间的关系有着深刻的科学意义，而且为网络的攻击和保护提供了有效的理论依据［5－7］.目前有关复杂网络鲁棒性的工作包括：基于渗流理论研究网络在删除部分节点后的连通性［8－11］；基于过载节点失效过程的网络上的动力学与网络结构的耦合［12－19］.然而，这些工作主要是关于单一网络的，有关相依网络鲁棒性的研究还比较少.2010年，Buldyrev等［1］在《Nature》杂志上首次发表了研究相依网络鲁棒性的著名论文，受到了极为广泛的关注.该文提出了一个简单的相依网络级联失效的模型，不但刻画了相依网络级联失效的过程，而且发现相依网络从连通态（有序）到破碎态（无序）是一个非连续相变过程，这与通常的复杂网络座逾渗模型的连续相变有着很大不同.随后的研究还发现降低相依网络之间耦合还可以使相变现象从一级相变变成二级相变，这类似于水在发生气液相变时的临界现象［3］.Huang等［4］研究了相依网络在单侧节点受到蓄意攻击下的鲁棒性，而董高高［20］研究了双侧节点受到蓄意攻击下的鲁棒性.然而，当前有关同时考虑相依节点对权重的攻击策略的研究还相对较少.本文研究了相依网络在几种攻击策略下的鲁棒性，并找出了最有效的攻击策略，从而发现了相依网络中最为脆弱的节点.

2 相依网络的蓄意攻击策略以及鲁棒性

2.1 相依网络的级联失效过程

相依网络可以形象地描述为相互依赖的系统，由两个网络A和B组成.每个网络内部的节点由连接边（connectivity links）连在一起，表示网络内部节点的连接关系.跨网络的节点由相依边（dependency links）连在一起，表示网络之间节点的相依关系［1，21］.当相依网络中A或B网络的节点受到攻击而失效的时候，网络A或B会破碎成几个碎片.该模型假定只有属于网络A或网络B极大簇（giant component）的节点能够保持功能，而属于其它碎片的节点会失去功能.假定网络A中部分节点受到初始攻击而失效，网络A会破碎为若干碎片，不属于A网络极大簇的节点也会失效.A网络中的失效节点也会导致B网络中相应的节点失效，从而导致网络B的破碎，不属于网络B极大簇的节点也因此失效.再进一步，B网络中的失效节点也会导致A网络中相应的节点失效，从而导致网络A再次发生破碎.如此反复进行下去，经历一定步数的迭代后（NOI），系统会达到稳定.当系统达到稳定时，只有属于互联极大簇（网络A中极大簇的节点和网络B中极大簇的节点完全是由相依边连在一起的）的节点才能保持功能.整个级联失效的过程，如图1所示［1］.图中，aij，bij（i，j＝1，2，…，n）分别表示网络A，B的节点.在初始的情况下，A网络的一个节点因受到攻击而失效；在阶段1，与该失效节点相连的边被删去，同时与之相依的B网络中的节点也因此失效，与之相连的边也被删除，不属于A网络极大簇的节点a11，a12失效；在阶段2，b21，b22因与失效节点a11，a12相依而失效，不属于B网络极大簇的节点b23失效；在阶段3，B网络中失效的节点b23又导致了A网络的a33节点失效，整个系统达到稳态.

图1 相依网络级联失效的迭代过程Fig.1 Iterative process of a cascade of failures

相依网络中互联极大簇是衡量相依网络在受到攻击后维持自身功能的重要指标，类似于渗流理论中的序参量极大簇，本文将互联极大簇标记为S.在接下来的部分，将重点研究相依随机网络在不同攻击策略下互联极大簇随着攻击强度的变化而变化的规律.

2.2 相依网络的蓄意攻击策略

相依网络在随机攻击策略下的鲁棒性已经有较为深入的理论研究，然而在相依网络中，一个节点的失效会导致与之相依节点的失效.因此，一个节点对于维持整个网络连通性的能力不仅与自身有关，而且与它相依的节点有关.本文对相依网络中相依节点对进行加权，这里的权重假定就是这对节点对于维持相依网络功能的重要性，然后依据它们的权重大小进行攻击.

攻击策略I：对A网络中节点度进行降序排列，攻击排序靠前的比例为1－p的节点，因此剩下比例为p的节点保留了下来.该策略仅仅考虑了单侧节点的度.

攻击策略Ⅱ：对网络A，B中相依边两端的相依节点对进行加权，第n对节点的权重是：Wn＝其中表示A网络中第n个节点的度表示B网络中第n个节点的度.然后依据权重对这些节点对进行排序，攻击排序靠前且比例为1－p的节点，保留比例为p的部分节点.该策略同时考虑了相依节点度的特性.

在这里，通过参数p可以调节对相依网络的攻击强度.在接下来的部分将展示网络的互联极大簇S随参数p的变化规律.这里研究的相依网络是由两个ER随机网络random networks）组成，两个网络中节点之间的相依关系是随机建立的，也就是说网络与网络之间相依节点度的相关性等于0.

2.3 相依网络在不同攻击策略下的鲁棒性

相依网络在随机攻击下，互联极大簇随攻击强度1－p的变化呈现一级（非连续）相变的行为，这与经典随机网络的座逾渗的二级（连续）相变有着很大的不同.文中图2～5的图（a）展示了相依网络达到稳态时的序参量S和参数p之间的关系；图2～5的图（b）展示了NOI与参数p的关系，图（b）中的插图展示了NOI在相变点处与网络规模N的关系.相依网络中两个网络的平均度都为〈k〉＝4，每条曲线都来自1 000次平均的结果.从图2（a）可以发现在不同的系统规模下，所有的曲线可以相交于一点.当系统的规模N趋向于无穷大的时候，可以认为互联极大簇S可以从此点跳到0，此点可以近似于一级相变的相变点.图2（b）展示了相依网络达到稳态时所经历的迭代步数（NOI）.NOI在相变点附近有一个峰值，当系统规模达到无穷大时，NOI所对应的p值就是一级相变的相变点.另外，还可以发现，NOI与网络规模N呈现幂函数的关系，也就是当N趋近于无穷大时，NOI也趋向于无穷大.对于相依的两个随机网络，网络破碎临界值的理论结果为pc＝2.455 407／〈k〉［1，22］，因此对于平均度为4的相依网络，其发生破碎的临界点pc＝0.613 8，通过模拟可以验证这一结果.

图3中（见下页），作者研究了相依网络在攻击策略I下的鲁棒性，发现了与随机攻击类似的一级相变的现象，但是临界点pc≈0.787，明显超过随机攻击的临界点pc＝0.613 8，这说明相依网络在蓄意攻击策略下变得更加脆弱了.

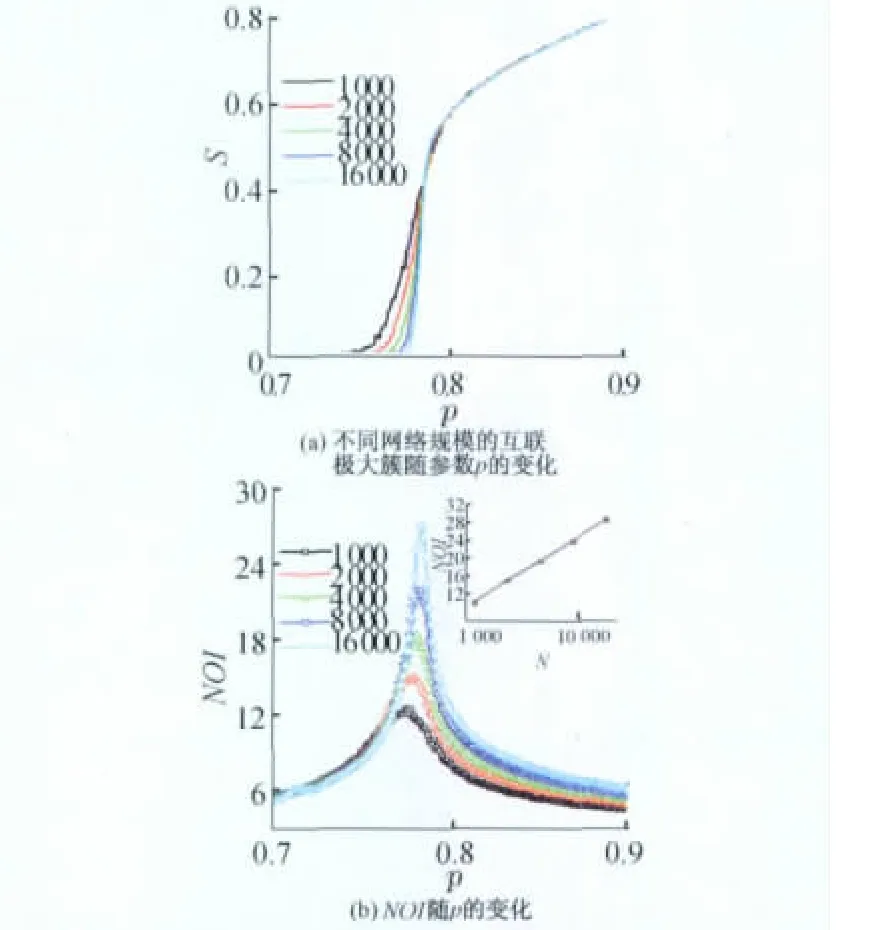
图3 攻击策略I下相依网络的鲁棒性Fig.3 Numerical simulations of interdependent networks under attack strategy I

图4研究了相依网络在攻击策略Ⅱ下的鲁棒性，同样发现了一级相变的现象.但是，临界点pc≈0.816，明显超过随机攻击与攻击策略I的临界点，这说明相依网络在此种攻击策略下变得进一步脆弱了.这个结果也证明了考虑相依节点对度之和的攻击策略比考虑单侧节点度大小的攻击策略更有效.

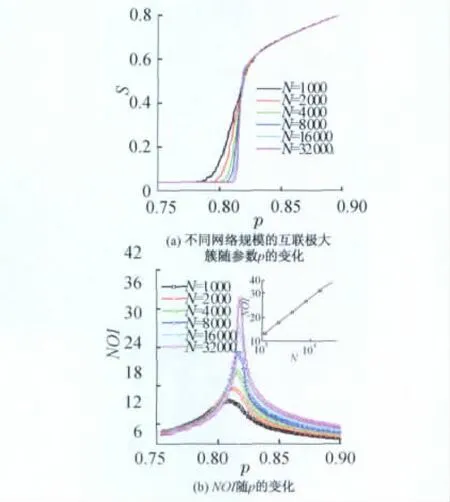
图4 攻击策略Ⅱ下相依网络的鲁棒性Fig.4 Numerical simulations of interdependent networks under attack strategyⅡ

图5研究了相依网络在攻击策略Ⅲ下的鲁棒性，同样发现了一级相变的现象，相变点pc≈0.818，与攻击策略Ⅱ的pc≈0.816类似.这个结果进一步证明了考虑相依节点对度特性的攻击策略比考虑单侧节点度大小的攻击策略更有效.

图5 攻击策略Ⅲ下相依网络的鲁棒性Fig.5 Numerical simulations of interdependent networks under attack strategyⅢ

3 结 论

本文比较了相依网络在几种攻击策略下的鲁棒性，发现了考虑相依节点对度特性的攻击策略比考虑单侧节点度特性的攻击策略更有效.这项工作对于理解相依网络级联失效的过程有着重要的作用，为找到相依网络的弱点并进行有效的保护和攻击提供了有益的提示.但是，本文仅仅研究了相依随机网络的鲁棒性，其它复杂网络如无标度网络和小世界网络的鲁棒性还有待进一步研究［5－7］.此外，目前研究的是相依节点度不相关的网络，今后还将研究相依网络度相关网络的鲁棒性［24］.对于正相关的网络，度大的节点往往与度大的节点相依.在随机攻击下，这样的网络会更加稳健［25］；在蓄意攻击下，这样的网络显然会更加脆弱.对于负相关的网络，相依节点对的度之和会变得更加均匀，这样导致在蓄意攻击下网络是更加脆弱还是更加稳健，这是一个值得研究的问题.还有需要注意的是，这里仅仅依据节点的度进行加权，是否有其它加权方法可以找到更加有效的攻击手段，如节点的介数，这又是一个非常值得研究的问题.

［1］ Buldyrev S V，Parshani R，Paul G，et al.Catastrophic cascade of failures in interdependent networks［J］.Nature，2010，464（08932）：1025－1028.

［2］ Havlin S，Araujo N A M，Buldyrev S V，et al.Catastrophic cascade of failures in interdependent networks［DB／OL］.［2010－12－02］.http：／／arxiv.org／abs／1012.0206.

［3］ Parshani R，Buldyrev S V，Havlin S.Interdependent networks：reducing the coupling strength leads to a change from a first to second order percolation transition［J］.Phys Rev Lett，2010，105（4）：048701.

［4］ Huang X，Gao J，Buldyrev S V，et al.Robustness of interdependent networks under targeted attack［J］.Phys Rev E，2011，83（6）：065101.

［5］ 汪小帆，李翔，陈关荣.复杂网络理论及其应用［M］.北京：清华大学出版社，2006.

［6］ Dorogovtsev S N，Goltsev A V，Mendes J F F.Critical phenomena in complex networks［J］.Rev Mod Phys，2008，80（4）：1275－1335.

［7］ 何大韧，刘宗华，汪秉宏.复杂系统与复杂网络［M］.北京：高等教育出版社，2009.

［8］ Cohen R，Erez K，Avraham D，et al.Resilience of the internet to random breakdowns［J］.Phys Rev Lett，2000，85（21）：4626－4628.

［9］ Callaway D S，Newman M E J，Strogatz S H，et al.Network robustness and fragility：percolation on random graphs［J］.Phys Rev Lett，2000，85（25）：5468－5471.

［10］ Cohen R，Erez K，Avraham D，et al.Breakdown of the internet under intentional attack［J］.Phys Rev Lett，2001，86（16）：3682－3685.

［11］ Stauffer D，Aharony A.Introduction to percolation theory［M］.2nd ed.London：Taylor ＆Francis，1992.

［12］ Motter A E，Lai Y C.Cascade－based attacks on complex networks［J］.Phys Rev E，2002，66（6）：065102.

［13］ Zhao L，Park K，Lai Y C.Attack vulnerability of scale－free networks due to cascading breakdown［J］.Phys Rev E，2004，70（3）：035101.

［14］ Zhao L，Park K，Lai Y C，et al.Tolerance of scale－free networks against attack－induced cascades［J］.Phys Rev E，2005，72（2）：025104.

［15］ Motter A E.Cascade control and defense in complex networks［J］.Phys Rev Lett，2004，93（9）：098701.

［16］ Wang W X，Chen G.Universal robustness characteristic of weighted networks against cascading failure［J］.Phys Rev E，2008，77（2）：026101.

［17］ Yang R，Wang W X，Lai Y C，et al.Optimal weighting scheme for suppressing cascades and traffic congestion in complex networks［J］.Phys Rev E，2009，79（2）：026112.

［18］ Wang W X，Lai Y C.Abnormal cascading on complex networks［J］.Phys Rev E，2009，80（3）：036109.

［19］ Watts D J.A simple model of global cascades on random networks［J］.PNAS，2002，99（9）：5766－5771.

［20］ Dong G G，Gao J X，Tian L X，et al.Percolation of partially interdependent networks under targeted attack［J］.Phys Rev E，2012，85（1）：016112.

［21］ Parshani R，Buldyrev S V，Havlin S.Critical effect of dependency groups on the function of networks［J］.P NAS，2011，108（3）：1007－1010.

［22］ Son S W，Grassberger P，Paczuski M.Percolation transitions are not always sharpened by making networks interdependent［J］.Phys Rev Lett，2011，107（19）：195702.

［23］ Gao J，Buldyrev S V，Havlin S，et al.Robustness of a network of networks［J］.Phys Rev Lett，2011，107（19）：195701.

［24］ 史定华.网络度分布理论［M］.北京：高等教育出版社，2011.

［25］ Buldyrev S V，Shere N W，Cwilich G A.Interdependent networks with identical degrees of mutually dependent nodes［J］.Phys Rev E，2011，83（1）：016112.