统计物理学基础研究新进展

王 馨， 张 江， 吴金闪

（北京师范大学管理学院，北京100875）

1 系统理论与统计物理学

系统理论与统计物理之间联系紧密，首先统计物理学所关注的系统一直是系统理论的重要研究对象，其统计物理学是系统理论研究方法的重要来源.系统理论是研究相互作用的大量个体构成的系统科学，研究这样的系统的描述方法、性质、结构与层次，功能以及干预调控.其中一个核心的研究方向就是构建从微观描述到宏观性质的桥梁，以及反过来从宏观现象探索微观机制.常常人们还额外关注系统宏观性质发生定性变化的现象.这样的现象称为涌现现象或者相变.在具体系统的研究中，这样的现象往往具有重要的实际意义.这些问题正好就是统计物理学的研究内容，只不过传统统计物理学更注重物理系统中这些问题的研究，而系统科学则研究更广泛的各个具体学科中的这样的系统.因此，统计物理学是系统科学，或者说是复杂性研究的研究方法的主要来源.另一方面，包含相互作用的大量个体的物理系统，自然也是系统科学的研究对象之一.

从系统科学的角度研究统计物理学更多地是从非平衡统计的角度展开.平衡态统计物理学给出一个这样的大图景（尽管作者个人不认为这样的图景能够从平衡态统计物理学得到，但是在此还是用通常的说法——“热寂说”）：在低温条件下，系统会产生结构；而在高温条件下，系统趋向于没有结构的各向同性状态.然而，结构的涌现是很多系统的普遍现象，尤其是在生物、社会、经济系统之中.那么，什么系统，在什么条件下会产生结构，自然就成了系统理论研究的核心问题.既然平衡态统计物理学给出了不一样的图景，那么Prigogine等就认为与外界存在能量流和粒子流，也就是开放性和非平衡性，是结构产生的根源.这个问题与从可逆动力学到不可逆热力学的问题也是联系在一起的.因此，非平衡与不可逆性，从系统科学创立阶段开始，一直是其最核心和最基础的研究问题.

2 统计物理学的基本问题及其研究进展的粗略图景

平衡态统计物理学的基本理论是系综理论.以哈密顿量H所描述的处于温度T的正则系综为例，平衡态统计物理学认为，其状态由Boltzmann分布

描述，其中，β＝1／kBT（kB为参数），归一化常数Z被称为配分函数.一个正则系综通常被认为是处于一个大热浴中的一个小系统，与热浴存在着能量交换但没有粒子交换.平衡态还表示，这样的一个小系统经过与大热浴的长时间接触，无论其初始状态如何，都会“演化”到一个稳定态上.这样的统计力学演化与基于第一原理（牛顿方程或者薛定谔方程）的动力学演化是不一致的.前者通常不可逆，存在稳定态；后者是可逆的，往往不能给出一个稳态.这就是著名的从微观可逆性到宏观不可逆性的问题.这就是统计物理学基本问题之一：平衡态如何从第一原理推导出来.基于第一原理的演化，或者说动力学演化遵循Newton方程或Schro¨dinger方程，统一记为

其中，ρ称为密度分布函数（经典力学）或者密度矩阵（量子力学），LH称为Liouville算符.它完全由系统哈密顿量H决定.

通常认为，这样的正则分布是可以从微正则分布——孤立系统的状态符合等能面上的等几率分布推导出来，因而，上面的问题就成了如何从第一原理得到微正则分布.由此，如果能够证明微正则分布或者找到系统出现微正则分布的充分必要条件，则正则分布也得到了证明.研究微正则系统比正则系统要简单得多，因为前者是孤立系统，而后者必须考虑热浴.因此，很多的工作都从动力学演化的角度来探讨微正则分布出现的充分必要条件.微正则分布是指与外界不存在能量与物质交换的孤立系统，其状态是给定能量所对应的等能面上的均匀分布.这是一个很可以理解的假设：孤立系统的能量自然是常数（其它的动力学守恒量也是常数，这会把等能面分成几个独立的部分，在此为简化问题假设没有这样的守恒量），因此系统只能处于给定等能面上；等能面上的各个点没什么不同，在不知道确切初始条件的情况下，也只能假设它们都等价了.在这方面，最近的研究表明，不用微正则分布，只要考虑了系统与热浴构成的大系统（有时候称为宇宙），大系统甚至处于纯态而不用处于微正则分布，对于绝大多数的纯态，子系统的约化密度矩阵都处于正则分布，这被称为正则典型性［1］.这个结果相当于用“绝大多数”纯态代替了微正则分布.这方面的研究看起来为统计物理学基本问题的研究开辟了一个新的方向，引起了很多研究者的兴趣.

然而，最近的研究注意到这样一个事实［2－3］：不增加任何别的假设，正则分布不能通过微正则分布（或者以上的绝大多数态）推导出来.通常教科书式的标准做法是把子系统和热浴一起看成一个孤立系统，然后从这个孤立系统的微正则分布，加上热浴的态密度是随着能量指数增长的假设，导出子系统的正则分布.注意，这个推导没有要求热浴自身处于热平衡态，只要求热浴和子系统构成的整体系统是孤立系统，符合微正则分布.尽管这个关于热浴态密度的假设也很可以理解，但是并不是所有的热浴都具有这个性质.是否只有这样的热浴才能驱动系统演化到热平衡，还是一个问题.对于考虑了正则典型性以后的表述，也就是说整体系统处于绝大多数纯态都可以（在同样的态密度假设下）得到子系统的正则分布，所要求的条件看起来弱了很多.但是，目前尚无法确定，正则典型性是否可以保证系统在演化过程中保持正则分布.

基于以上两方面的原因，于是有研究者就试图直接从系统与热浴耦合的整体系统出发，来讨论系统演化到定态是正则分布的充分必要条件.鉴于正则分布在描述实际系统上很高的适用性，这样的条件应该不是非常特殊.研究者们希望证明类似这样的一个定理：只要系统哈密顿量满足某些条件，热浴哈密顿量满足某些条件，相互作用形式满足某些条件，热浴的大小（粒子数、自由度数目）满足某些条件，热浴的初始状态满足某些条件，系统就会在整体系统的动力学演化下趋向平衡.当然，如果有必要，系统的初态也可以做约束.所有的这些条件越容易满足越好，而且最好也是必要条件.

回答这个问题是几代物理学家的梦想.20世纪60年代发展起来的投影算符方法，可以从整体系统的动力学方程得到子系统的有效动力学方程，通常具有如下形式，也被称为动理学方程

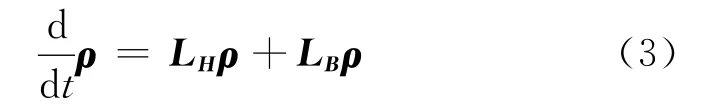
它在第一原理动力学方程的基础上增加了一项来自于热浴的算符LB，同时在某些条件下也有可能改变原来的子系统本身的算符.

从这个方程出发，假设热浴很大，而且处于热平衡态，以至于改变子系统状态时其自身状态不变，那么从得到的动理学方程可以计算出定态解，而且这个定态解正好就是热平衡Boltzmann分布.也就是说，至少有一个充分条件：处于热平衡的理想无限大热浴，弱耦合（耦合强度小，Markovian近似适用，耦合项的二阶微扰适用），则子系统符合热平衡分布.当然，这个结果并没有回答前述统计物理学的根本问题——从第一原理推导出热平衡分布.实际上，只是从一个热平衡（热浴的）导出了另一个热平衡（子系统的）.甚至这个结论本身，也还有很多欠缺之处：有限但是非常大的热浴是否可行，Markovian近似和二阶微扰是都必要等.更一般地说，热浴是否必须处于平衡态，处于别的某种状态是否也可以导致相应的定态（当然此时就不一定是热平衡态），还是说热平衡态具有某种特殊的稳定性，只有它才能从热浴“传到”子系统上去，这些问题都还没有回答.

最近有研究者宣称他们已经回答了这个问题：只要满足非常简单的条件，热浴的自由度大于子系统的自由度［4］，子系统就会趋向定态，而且在满足进一步的条件下，这个定态就是热平衡态.然而，这些作者判断子系统趋向定态的方法是定义子系统密度矩阵的长时平均

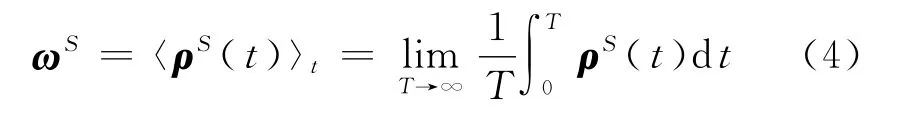
其中，ρS＝trB（ρSB）为热浴部分自由度求迹以后的密度矩阵.文献［4］的作者们发表了很多相关的文章，有兴趣的读者可以做一个系统地跟踪阅读.如果ρS存在长时稳态极限，那么上面定义的极限确实是其长时极限.不过，反之就不正确，也就是说，就算如上定义的极限存在，也不能肯定ρS存在长时稳态极限.有关这方面的反例以及相关工作正在展开.

统计物理学的第二个基本问题是系综理论为什么能够描述热力学测量.系综理论是一个关于状态分布函数的理论，也就是一系列系统构成的整体系综的理论，热力学测量原则上是在测量一个演化的系统或者一个处于定态的系统.一个由概率论所描述的随机个体，某个概率分布描述了这个个体，含义是从对大量个体的独立测量构成的整体来看，测量的统计特征与分布函数相符.但是，在热力学测量中，通常只在一个系统上做测量，最多重复很少的次数，就把测量量与基于分布函数的计算量相比，而且符合得很好，为什么？通常统计物理学教科书的回答是：对于处于热平衡的系统，其长时平均等于系综平均.然而，通过对具体系统的计算，发现实现长时平均等于系综平均所需要的时间（以后称为回复时间，相当于遍历时间的尺度）远远大于实际测量时间［3］.这使得这个曾经认为已经得到回答的问题成了新问题.本文初步研究发现，如果只考虑系统自身的动力学演化，回复时间确实非常长，但是考虑子系统与热浴耦合之后的动理学方程，这个回复时间就小得多.因此，可以认为，热力学测量就是对分布函数的多次抽样，在每一次抽样之后，系统都要经过一个回复时间来重新回到成为平衡分布中的一个样本点，而这个回复时间不是完全由系统自身决定的遍历时间而是由系统和热浴共同决定的回复时间.目前，具体系统上的计算还在进行中.

统计物理学的第三个基本问题是如何处理非平衡定态，这也是本综述的重点.非平衡定态的计算是研究输运问题的基础.考虑例如热输运问题，一个准一维系统连接到两个不同温度的热浴上，经过一段时间，系统到达定态，其上有热流通过.希望能够计算热流与温度、温度差、系统材料之间的关系，还希望能处理电流、粒子流、自旋流等输运现象.更广义地说，结构的产生，也是系统的非平衡定态的性质.因此，对非平衡定态的描述方法的探索是系统科学基本理论研究的一个非常重要的方面.

如果有第一个问题的完整答案，这个问题也就差不多解决了.既然知道某种条件下耦合到一个大热浴的子系统会演化到平衡态上去，只要让这个子系统耦合到两个大热浴，那么可见子系统就会演化到一个新的定态上去，而这个定态就是要找的非平衡定态.但是，没有这样的一个充分必要条件，因此，也不能从根本上解决这个问题.换一个角度，没有解决平衡态的由来这一根本问题，这并不妨碍用系综理论来计算平衡态物理量.同样，对于非平衡定态，也希望先得到一套可计算的框架，然后有可能的时候再回去解决根本问题.

在这样一个指导思想下，发现有可能推广投影算符方法到非平衡态的计算.从耦合到单个热浴的子系统的动理学方程，可以类似地得到耦合到多个热浴的子系统的动理学方程，然后求解这样的动理学方程的定态.这个想法首先由日本学者Saito在耦合到谐振子浴的一维谐振子链上实现［5］.在这个工作中，Saito确实发现了非平衡定态，得到了半解析半数值的解，注意到一维谐振子链其实可以转化为无相互作用系统，这使得Saito能够求解这一动理学方程.对于相互作用系统费米子系统，这个关于密度矩阵的方程有4N个变量；对于相互作用系统波色子系统，这个方程有无穷多个变量.求解这样的方程是一件非常困难的工作.后来的工作在运用这个方法讨论具体系统和具体物理问题的同时，都把大量的工作用在了寻找求解这一方程的高效方法上.目前来说，除了Runge－Kutta方法、直接对角化等直接方法之外，还发展了基于局域算符展开的密度矩阵重整化方法［6］、Monte Carlo方法［7］、Green函数方法［8－9］、相干态量子随机微分方程方法［9］等一系列间接方法.本文将在下面展开论述其中一部分方法.这些方法的对比，以及在具体系统上的应用等问题都还没有得到深入的研究，在这些方面还有大量的工作要开展.如图1所示的是连接到两个热浴的准一维系统.其中TL，TR为左右热浴的温度，jh为流密度.宏观输运定律假设系统上存在着温度或者电压的梯度，而从微观角度希望能够从第一原理出发，计算系统的稳态以及各个物理量.

图1 连接到两个热浴的准一维系统Fig.1 Sketch of a typical setup of heat conduction

在具体物理问题的研究方面，正常导热性的充分必要条件，也就是研究在什么样的系统上热传导满足傅里叶定律，一直是非平衡统计研究的一个重要方向.傅里叶定律是一个适用于宏观客体的实验定律，其经典力学基础和量子力学基础都是不明确的，适用范围也不明确.费米等在经典FPU模型上的工作，以及后来大量的在FPU上的工作，都企图从动力学演化的角度回答这个问题.但是迄今为止没有找到正常热导的充要条件，或者从动力学演化到热平衡分布的充要条件.当然也得到了一定的结果，例如完全可积系统不能实现热平衡，没有正常热导.其物理图像可以作以下理解：完全可积系统存在非常多的动力学守恒量，也就是说系统可以看成独立的很多个本征运动模式，每一个运动模上的能量是独立的，不能相互混合传递，因此不能实现热平衡.在仅考虑动力学演化的范围内，这个图像似乎是有道理的.然而，所有的数学形式以外的物理学理解，也就是所谓的物理学图像，都可能是欺骗性的.例如量子力学是不是要有现实性，以及什么样的现实性，等等这样的问题，都可能是用人们用习惯了经典力学图像的大脑来理解量子力学世界的结果.在这里，唯一可靠的就是Hilbert空间的结构和薛定谔方程本身，除了数学结构，没有独立的有意义的非欺骗性的“物理图像”.人们能够问的问题是为什么量子力学的实验就要求有这么奇怪的数学形式，而不是形成所谓的量子力学的独立于数学形式之外的物理图像.回过头来看这个关于可积性的物理图像，如果系统存在与外界的耦合，而这个往往是讨论趋向热平衡或者热传导必须的，这些不能直接混合传递的本征模之间，完全可以通过与外界交换能量来实现间接地混合与传递.因此，不考虑热浴，不考虑动理学演化的关于热传导或者趋向热平衡的讨论是不完整的.从这个角度来说，有了这个非平衡定态研究的框架，才能够正确地讨论正常热导的充分必要条件.在经典低维系统的正常导热性方面，基于具体系统的研究结果，中国学者赵鸿等提出了动量守恒是反常热传导的根源的假说，以及最近关于非对称势导致正常热传导的理论.在此，主要关注量子系统，对经典系统有兴趣的读者请参考相关的综述文献［10］.

另外一方面，本文还可以用同样的框架研究电流与自旋流的问题.目前电子输运的实验研究已经表明在微观尺度，欧姆定律不成立，电阻与导体长度之间没有正比关系.这就要求有一个基于第一原理的新的处理电子输运过程的框架.除了动理学方程这一方法之外，通常（或者说更经常地）可用另外一套半原理半唯象的处理方法：Landauer－Buttikker公式［11］以及非平衡格林函数理论（NEGF）［12］或者Kubo（久保）公式［13］.Kubo公式只适用于无限大系统，近平衡，而且是外势驱动的输运问题［14］.在此本文不展开讨论.Landauer－Buttikker公式的物理图像是零温无相互作用系统的输运，可以用两个有偏分布函数来描述.假设左端化学势μL比右端μR高，那么右行粒子（来自于左端电极）占满到μL的能级，而左行粒子占满到μR的能级.自然右行粒子多于左行粒子，算出这个差别和相应的电荷，就得到了电流.这个方法的基本计算是先找到所有的散射波函数，然后按照各自的分布把左行和右行散射波函数的电流加起来，即

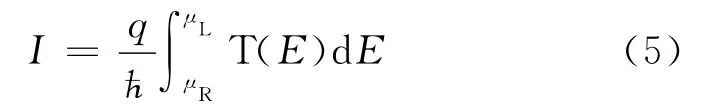
式中，q为电荷量；ħ为常数；T（E）为能量是E的右行散射波函数的透射系数.通常在计算这样的散射波函数过程中，还假设这个准一维系统是无穷长的.在这个框架下面，如果要问子系统的状态（由约化密度矩阵描述）是什么，那么它可以认为是如下整体系统的密度矩阵的约化：整体密度矩阵是左行部分和右行部分的直积，其中左行（右行）部分占满到μR（μL）的能级.在这个理论框架中，这样的密度矩阵是一个假设，尽管有道理也可以理解，但不是从第一原理推导出来的.实际应用中，人们发现对大量的系统，这个理论与实际测量符合得比较好.这是针对无相互作用子系统的理论，考虑到相互作用时，这个理论就不适用了.一个代替它的理论是NEGF.NEGF是一个微扰计算理论，没有非微扰形式.从不相连的两个半无穷长链（每一侧的链都有自己的温度和化学势，因而可以算出自己的格林函数）出发，把连接部分当成微扰项加入系统，然后计算这个微扰对系统格林函数的影响.由于系统在微扰前后的定态上有定性区别，必须要用闭路格林函数来做微扰计算，而不是通常的场论微扰展开方法.这个理论也是经验性的，尽管在无相互作用系统上它被认为与Landauer－Buttikker公式等价.考虑一个电压线性下降的导体，不知道经过微扰计算，能不能从阶跃函数型的电压降得到线性下降的电压降.当然，这个方法的优点是，可以利用格林函数的方法直接研究相互作用的效果.实际计算过程中，对于相互作用往往要加入额外的近似，例如Hartree－Fock近似、集团展开等.这对此方法的精度带来了额外的影响.目前，在某些系统上，这个方法的表现还可以，但是在另一些系统上计算结果存在数量级上的差别［15－16］.用这个非平衡定态计算的一般框架，就可以直接处理相互作用系统，而且避免产生两重微扰的问题.再加上这个框架基本上是第一原理性的，不是通过微扰形式定义的，也可以为改进和检验以上方法提供参考.

以上简略地介绍了统计物理学基础研究的大图景以及输运问题的基本处理方法.然而，综述以非平衡定态的框架来研究输运问题是本文的重点，因此，后面将集中在这个方面，而不再涉及处理输运问题的其它方法.另外，在介绍完这个基本框架之后，在最后部分本文也会提到这个计算框架，也有助于解决统计物理学前面的两个基本问题.统计物理学，乃至整个物理学的中心问题之一——如何处理相互作用的多体系统，也会是贯穿整个综述的另一条线.

3 非平衡定态计算的基本框架

首先，简单地介绍一下投影算符技术和动理学方程方法，然后推广到应用于输运问题的情形；其次，举几个研究实例，展示这个基本框架；最后，将在简略地介绍几个计算方法的基础上，详细地阐述其中几个高效的计算方法.

3.1 投影算符技术与动理学方程

投影算符技术的细节可以参考Kubo的经典统计物理学教材［17］.其基本思想是从子系统与热浴的整体动理学方程出发，积分掉热浴的自由度，得到子系统的约化密度矩阵的有效运动方程.考虑整体系统

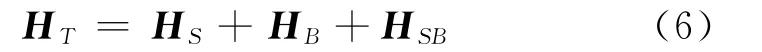
式中，HS，HB为子系统和热浴的哈密顿量；HSB为子系统与热浴之间的耦合项.整体系统的密度矩阵ρT满足方程式（2），其中，用到的Liuville算法是整体系统

定义子系统约化密度矩阵

式中，trB为在热浴B的状态空间作求迹运算，对于定义在子系统上的物理量AS，有

因此，只要能够求解ρ而不用整个ρT，就可以知道所有子系统上的观测量.定义投影算法

可以检验P确实是投影算法P2＝P，定义Q＝IP，其中I是单位算符.可由式（7）得到PρT和QρT的方程

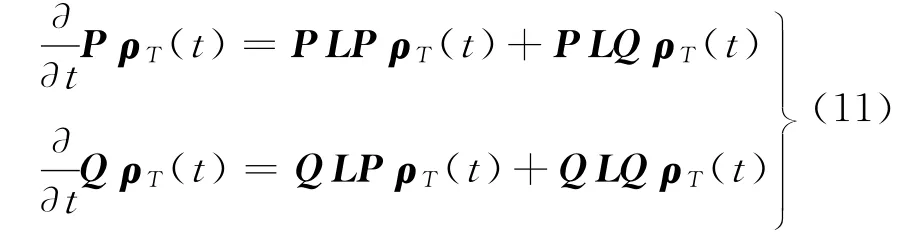
第二个方程可以形式上求解，然后代入第一个方程，结合初始条件

得到

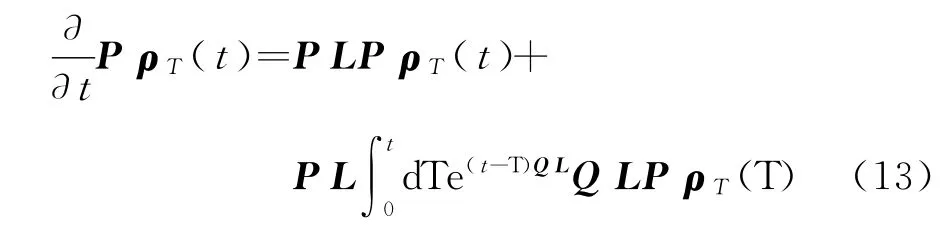
这是一个关于ρ的方程，当然其中还有整体系统的Liuville算符项L以及算符Q.这个方程描述了依赖于历史的非Markovian过程：方程中包含PρT（T）的积分.如果只关心定态而不是暂态的问题，可引入Markovian近似（粗略地说是让t→∞，ρ（t－T）→ρ（t））来大大简化这个方程.另外，指数上的L算符也很难处理，将其拆分成几个部分，例如

e（t－T）QL＝e（t－T）（1－P）L＝e（t－T）L（1＋O（P L））（14）然后在合理的条件下只保留第一项.对于方程，这相当于保留到耦合项的二阶微扰.细节请参考文献［9，17］.考虑这两个假设之后，这个方程可以得到进一步简化.下面以二次量子化形式下产生湮灭算符形式的哈密顿量为例，写出这一方程简化以后的具体形式，同时将方程推广到多个热浴的情形.

考虑准一维子系统与多个热浴通过第ν个格点与第ν个热浴耦合，其中，第ν个热浴的参数为温度Tν，化学势μν，耦合常数Vk，ν和λ，得

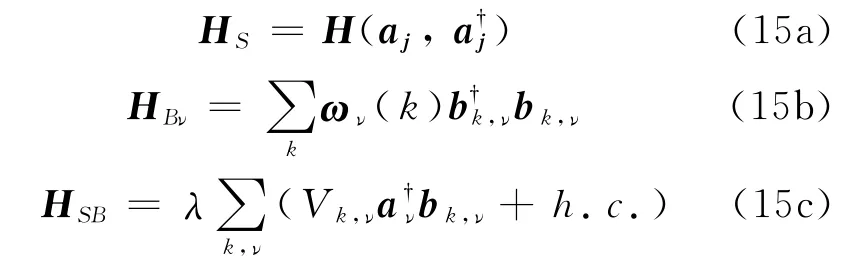
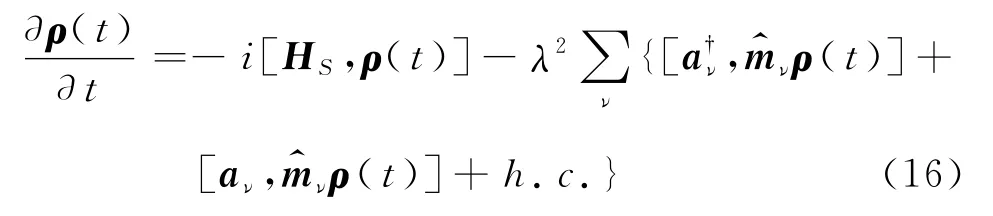
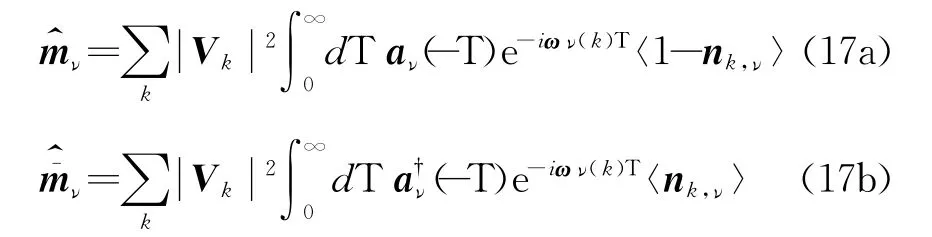
在这里aν（T）＝eiHSt aνe－iHSt是算符aν的Heisenberg绘景形式.这里已经作了Markovian近似，并只考虑了耦合项的二级微扰.这个方程有时候也被称为Redfield方程（RE）［18－20］.有关非平衡定态的计算可以直接从这个方程开始.这里nk，ν是第ν个热浴的第k个模上的平均粒子数

其中，±分别对应着费米子和波色子热浴.为简单起见，以后在不引起混淆的情况下〈nk，ν〉直接记为nk，ν.与孤立系统的动力学方程相比，这个考虑了热浴的动理学方程仅仅多了后面的有关算符和的项，而且所有热浴的信息都包含在这些算副符中，因此，称这些算符为热浴算符.下面对具体系统给出几个热浴算符的例子，并作简单计算来阐述一个需要注意的细节.

3.2 举例

从简单到复杂，从平衡到非平衡作几个具体系统的计算.一方面，用实际系统实现了上面的一般理论的计算；另一方面，从这些例子中将得到一些定性的结论.这些结论对于将投影算符方法推广到非平衡系统是有意义的.

3.2.1 单热浴中的单格点费米子系统：直接求解

考虑由哈密顿量描述的如图2所示的单格点费米子模型

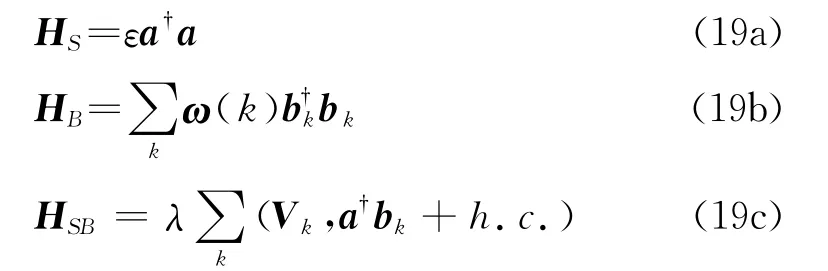
对此得到动理学方程

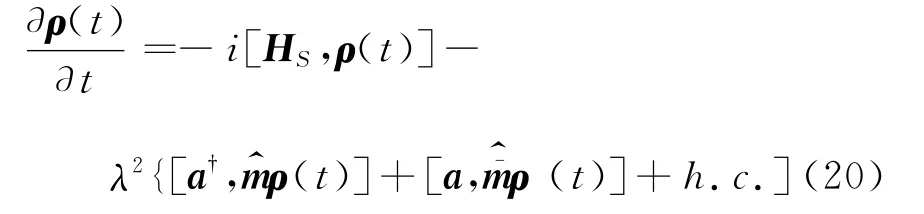
和热浴算符

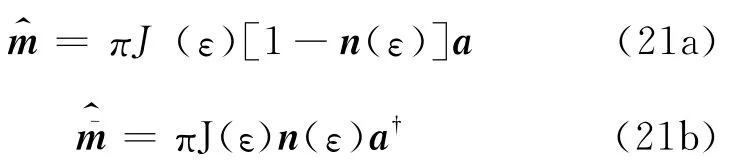
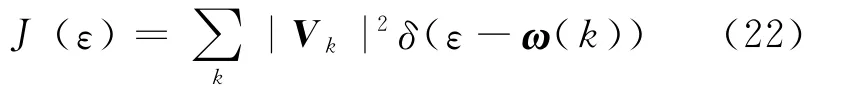
这个组合表达式J由热浴的态密度、子系统本征模的能量以及耦合常数决定.

图2 单格点系统与单热浴耦合草图Fig.2 Sketch of a one－site system coupled to a heat bath

在单格点单本征模系统上，为简单计，设J＝1.定义密度矩阵

并把它表示成为一个4维向量

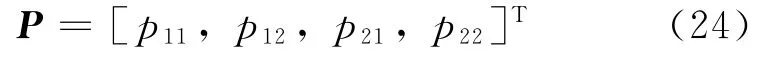
湮灭算符与热浴算符可以表示成

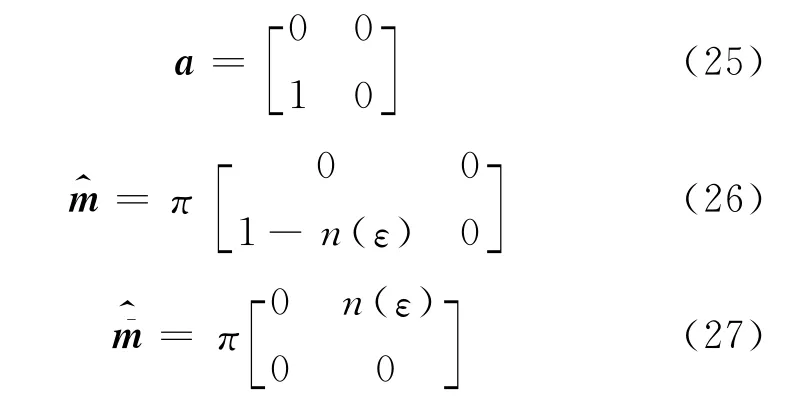
把这些算符以及密度矩阵都代入式（20），可以得到

其中，Γ是一个4×4的矩阵，或者更一般地说是一个4N×4N维的矩阵.对于一个N格点的无自旋费米子子系统，这个方程的演化完全由Γ的谱决定，其定态P0由零本征值对应的本征向量给定，即

当且仅当Γ只有一个零本征值，而且其它本征值小于零时，方程具有唯一定态解.对于单热浴中的单格点费米子系统可以验证Γ满足这一条件.计算出来的平衡态也正好是巨正则系综对应的热平衡态同时，注意到λ与定态没有关系，以后会看到，非平衡

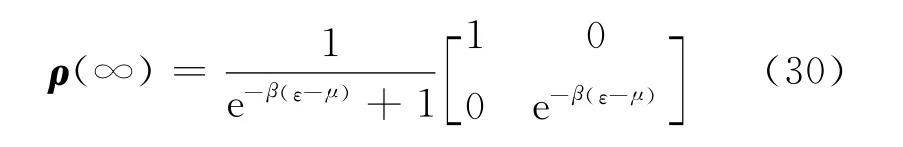
态的细节与λ是有关系的.还要注意到对于平衡定态，系统自身动力学LHs项不直接进入动理学方程（它决定采用什么基矢——它们是HS的本征态）.它实际上只影响HS表象下密度矩阵的非对角项，而平衡态这样的非对角元素为零.这一点，在非平衡定态中，也会发生变化，对系统自身动力学LHs将有重要影响.由于空间维数的问题，波色子系统的相应计算会更复杂，但是整体框架和物理图景是一致的.

单格点系统的Redfield方程式（20）可以抛开热浴算符和，写成

这一形式被称为Lindblad方程.有的研究者也用这个方程而不是Redfield方程来研究非平衡输运现象.可以看到对于单格点系统，两者是等价的.但是，以后会看到对于多格点系统，Lindblad方程实际上是在Redfield方程的基础上引入了进一步的近似：称之为弱连接条件或者局域哈密顿量条件.称这个推广以后的对于多格点系统的Lindblad方程为局域算符Lindblad方程（LOLE）.在弱连接条件不满足的情况下（格点之间的hopping强度大于或者类似于格点上粒子的能量），Lindblad方程甚至不能给出正确的平衡态.

3.2.2 单热浴中的双格点费米子系统：选择RE而不是LOLE

考虑如图3所示的单热浴中的双格点紧束缚模型

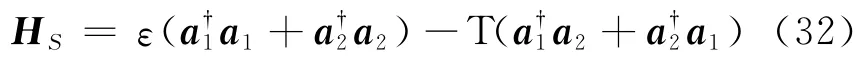
其中，格点1与热浴连接

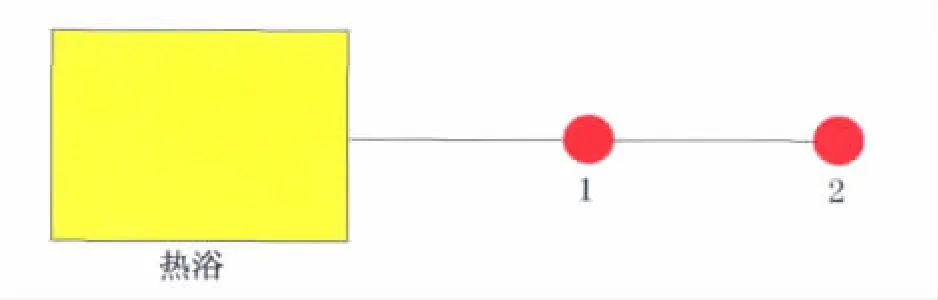
图3 单热浴中的双格点紧束缚费米子系统草图Fig.3 Sketch of a two－site system coupled to a heat bath

按照方程式（13），有

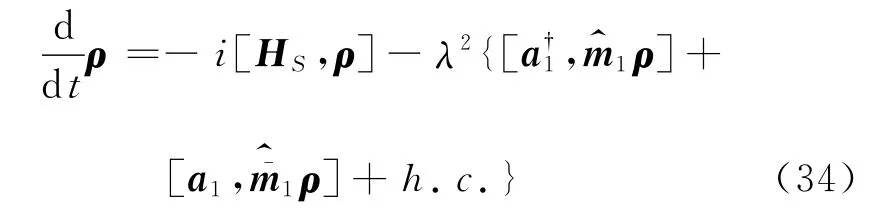
其中，热浴算符为

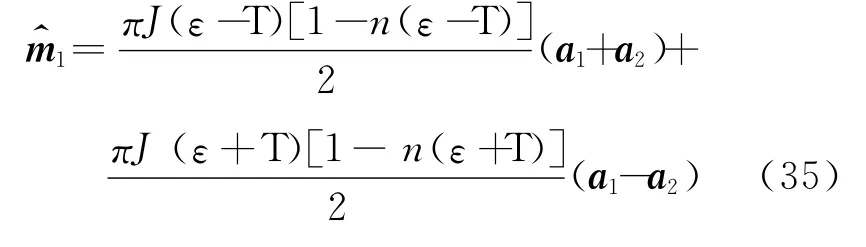
有的研究工作对于多格点系统，还是简单地直接推广单格点系统的Lindblad方程式（31），即

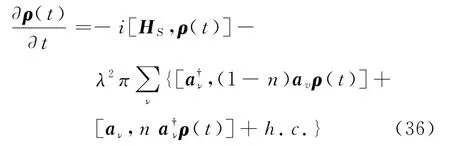
这里平均粒子数由ν格点的参数（化学势、温度、onsite能量）决定：n＝n（εν；Tν，νν）.可以看到这时Redfield方程与Lindblad方程并不相同.后者是前者在弱连接（T≪ε）下的近似.再看两个方程（具体来说这里就是比较式（34）与式（36）的特例——ν＝1的情况）给出的定态是不是相同，并把定态与热平衡分布做比较.

取上述系统HS的本征模

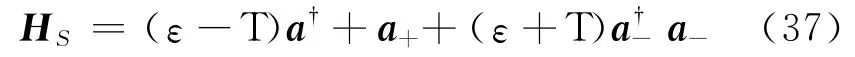
其中

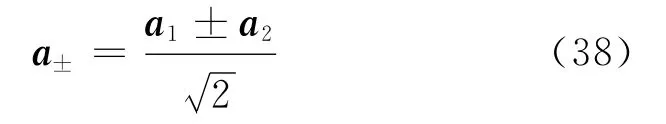
利用这些本征模的粒子数表象｜n＋n－〉，具体来说｜00〉，｜10〉，｜01〉，｜11〉相应本征值E1＝0，E2＝ε－T，E3＝ε＋T，E4＝2ε.定义这个表象下的密度矩阵

并把它表示成为一个16维向量

写出这个表象下的产生湮灭算符与热浴算符，代入式（34），可以得到形如式（28）的线性方程.求解这个方程可发现，定态P0也正好是热平衡

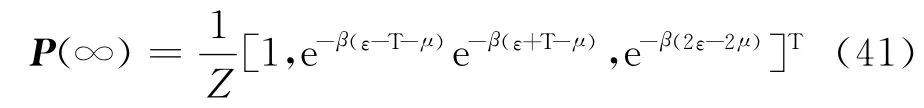
其中，Z＝1＋e－β（ε－T－μ）＋e－β（ε＋T－μ）＋e－β（2ε－2μ）

对于Lindblad方程式（36），也计算了其稳态并与平衡分布做了对比.两个分布函数ρA与ρB之间的距离定义为

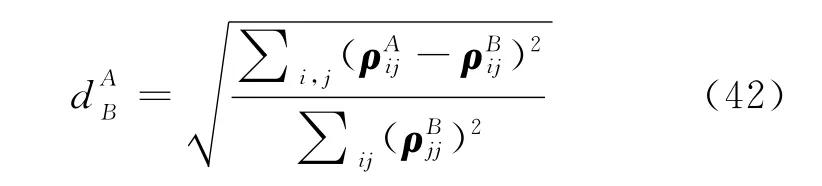
可以看到，只有在T≪ε时Lindblad方程的解比较接近Redfield方程的解，而后者就是热平衡分布.随着t的增大，其距离也逐渐增大.基于这个结果，作者认为，在非平衡态的研究中，应该优先考虑Refield方程.两者在平衡态下的对比详见图4，其中，Redfield方程给出了正确的平衡态.

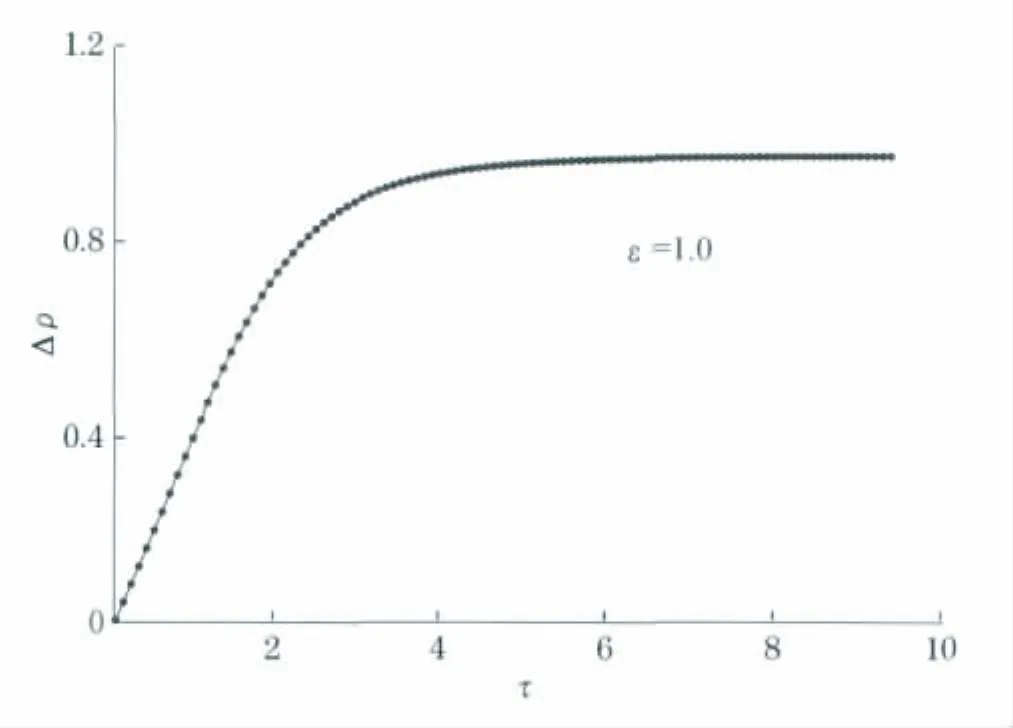
图4 Redfield方程与局域Lindblad方程在平衡态下的对比Fig.4 Stationary states from the local－operator Lindblad equation compared against those from the Redfield equation

3.2.3 双热浴中的双格点费米子系统：非零非对角元

同样的思路可以处理多个热浴中的子系统，研究其定态.事实上式（16）就可以直接用于多热浴的计算，只要注意热浴算符和，用第ν个热浴的温度、化学势等参量.以下计算双热浴中的双格点费米子系统.

如图5一个双格点系统耦合到两个热浴，Redfield方程为

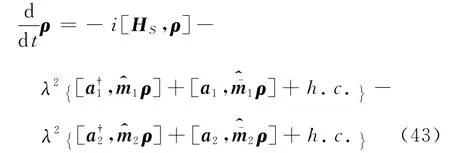
其中，用到新的热浴算符

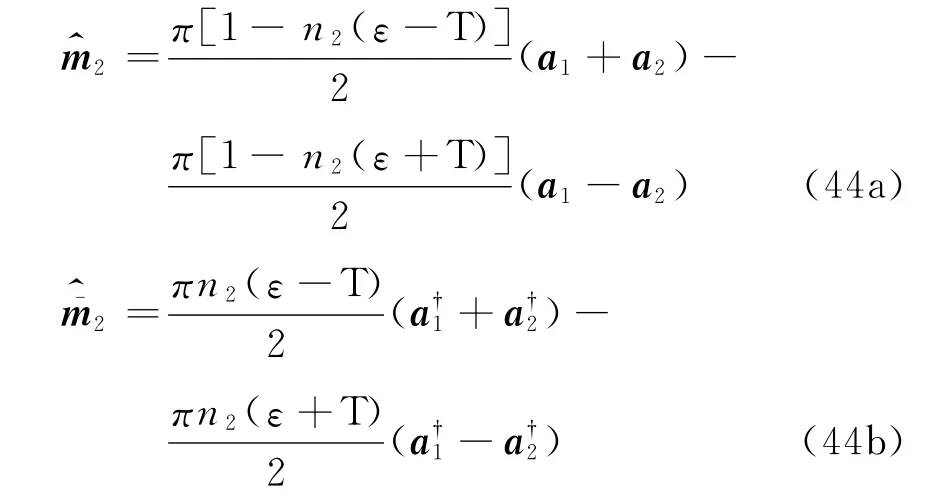
如果两个热浴的温度与化学势相同，重复上面的计算，可发现相同的热力学平衡态.

图5 双热浴中的双格点费米子系统草图Fig.5 Sketch of a two－site system coupled to two heat baths

那么一个自然的问题就是，如果两个热浴有不同的参数，还能不能得到稳态；如果得到了稳态，这个稳态是否就是要寻找的非平衡定态.对此，没有一般的理论来支持这个猜想.这个动理学方程也不是第一原理性的.在第一原理动力学方程之上，还加入了诸如无限大热浴、热浴处于热平衡、Markovian近似、耦合项的二级微扰等很多近似.因此，不能保证这个动理学方程的处理方法就能给出正确的非平衡定态.然而，包括前面提到的Landauer－Buttikker公式，NEGF等同样非第一原理性的方法，都不能写出非平衡分布的一般形式.既然这个动理学方程方法在合理的条件下能够给出正确的平衡态，有理由推广，在相应的条件下，其稳态也可以是非平衡定态.真实情况如何就只能依赖于实验检验了.

现在可以让两个热浴具有不同的温度TL和TR，重复以上的计算.在此，不再详细写出计算过程.从计算结果可以看到密度矩阵的非对角元，此时非零，这一点与平衡态是不一样的.图6所示Redfield方程的解与平衡态对比.当δT＝0，也就是平衡态，两者完全一致.对于非平衡态的非对角元非零，对角元也与平衡态的值不同.其中平衡态取与平均温度相对应的Boltzmann分布.

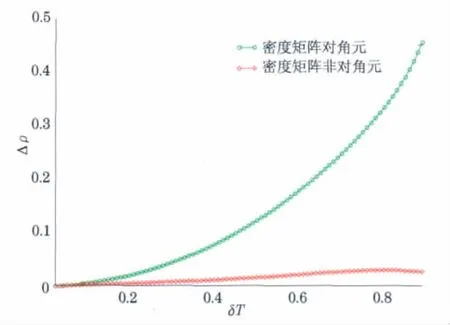
图6 Redfield方程解与平衡状态对比Fig.6 Comparison between the solution of Redfield equation and equilibrium

下面将这样的一个框架用来计算多个热浴中的N－格点系统.

3.3 基本框架的计算问题

总结求解Redfield方程的方法：

a.求得aν，a†ν的动力学演化，并进而得到热浴算符的表达式.这一步通常需要HS的谱展开.对于N－qubit系统，这是一个2N维本征值问题.

b.得到矩阵Γ的表达式.这是一个4N维的矩阵.

c.求解矩阵Γ的零本征值对应的本征向量.这是求解一个4N维矩阵的本征值.

可以看到，直接求解方法要比求解Schro¨dinger方程困难得多.Schro¨dinger方程的求解已经需要用到各种各样的近似与间接方法，更何况Redfield方程.因此，发展和运用这一基本框架的重要问题，就是研究出高效率的求解上述方程的方法.

在平衡态统计力学中，有量子Monte Carlo方法、以无相互作用系统上的精确解为基础的微扰论（Feynman图展开、BBGKY链）、密度矩阵重整化、密度泛函理论等方法来处理相互作用系统.那么，对于非平衡Redfeild方程，能否也研究一套方法，先简略地总结一下他人提出的方法，然后再重点介绍一下自己的工作.

4 相互作用系统非平衡定态的计算技术

4.1 现有方法小结

量子主方程，不管是Redfield方程还是Lindblad方程，都是一阶微分方程，记为

可以用直接积分的方法求解.这样的积分求解方法包含对一般系统都是用的Runge－Kutta方法（RK）、short－iterative－Arnoldi（SIA）传播子、短时Chebyshev多项式（CP）传播子、Newtonian多项式传播子、以及辛积分子（symplectic integrator）方法.对于这些方法，文献［21］做了比较和综述，在此仅做简单介绍.

Euler方法就是直接计算数值积分，例如ρ（t＋δt）＝ρ（t）＋Lρ（t）δt.它有正比于（δt）2的误差.RK就是用更合理的多次迭代方式，在不增加太多计算量、不用改变步长的前提下，减小误差，例如将一步的迭代改成两步、四步或者更多步.这样的计算方法对于很多的演化方程都是适用的，但是它并没有利用动理学方程是线性的这一特征.这个方程的计算复杂度主要取决于步长，每一步的计算需要处理2N矩阵的相乘运算.

线性微分方程存在一般解

所以，只要知道算符（有时候称为超算符，因为算符通常指作用在波函数上的线性映射，而L作用在密度矩阵，也就是通常所说的算符上）L的本征向量与本征值（当说超算符的本征态和本征向量时，把超算符看在作一个大矩阵，例如方程式（28）中的Γ.在这个意义上，把Γ与L等同，P与ρ等同），就可以知道一切

特别地，如果只研究定态，则

其中要求

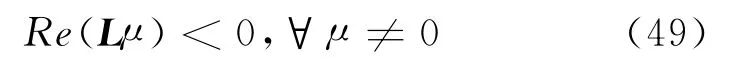
只有

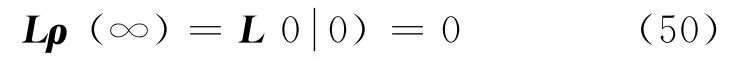
所以，问题转化为求4N维矩阵的零本征值问题.考虑归一化条件

可以用tr（ρ）替换L的任意一行，不妨说第一行，然后方程的右边也需要作相应的变化，也就是第一个元素为1，得到

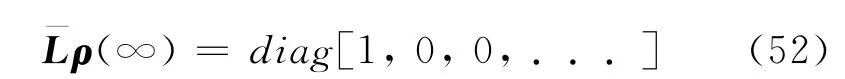
这里diag是指把所操作的向量放在对角元上形成一个矩阵.直接求解4N维线性系统的零本征向量或者线性方程的解，尽管数值意义上精确，但仍然是一个困难的问题.下面一类近似解法的基本想法是用更简单高效的方法来近似代表演化算符eLt.细节请参见文献［21］以及其中相应的文献.下面以SIA为例，介绍这些方法的思想.从一个t时刻的状态ρ（t）出发，构造一个Krylov空间，就是做n次重复计算Lnρ（t），记录这些矢量组成的空间.在n维这个子空间内，算符L拥有的形式为

其中，矩阵V可以由Lanczos方法在构造以上Krylov空间的过程中得到.下一步，在子空间内对角化算符l.记对角化以后的算符为L，变换的矩阵为S，则

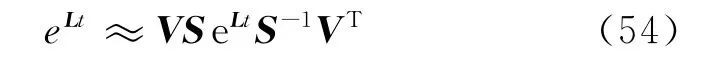
这样，就可以得到密度矩阵演化过程的近似解.在这个方法中，还是要计算很多次4N维矩阵的代数运算.

另一个经常使用的方法是随机波函数方法［7］.其基本思想是利用一系列波函数来等价地代表密度矩阵

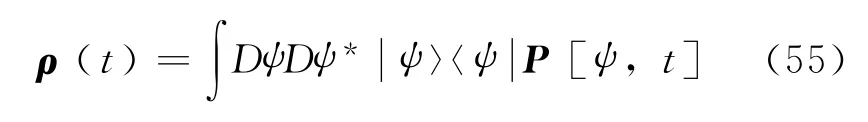
然后用这一系列波函数的演化来代替密度矩阵的演化.在这些波函数的演化中，往往会出现跳跃项等需要随机过程来模拟的动力学，而不再是厄米算符所描述的幺正演化.这个方法的算法复杂性相当于求解Schro¨dinger方程再加上随机跳跃过程，也就是说大概相当于求解2N维的线性系统.

以上这些方法，对一般的量子主方程都是适用的，没有要求方程具有任何特殊结构.最近，Prosen等提出了针对密度矩阵的tDMRG方法［6］，但是只能用于局域算符Lindblad方程.其中用到了演化算符的局域展开，这一点在Redfield方程上不能实现.这个方法对于无相互作用系统，相当于把2N的线性系统转化为N2维的问题.对于相互作用系统，这个方法的效率Prosen等还在进一步研究中.

下面主要介绍本文提出的两个方法：基于Green函数的非平衡BBGKY链方法和基于量子相干态表象的量子随机微分方程方法.

4.2 类BBGKY方法

从处理平衡态的多体系统的技术［22］知道BBGKY链方法与Feynman图微扰展开或者Dyson方程等是等价的［23－24］.对于无相互作用系统，Wick定理表明单粒子Green函数的方程式封闭，而且只要知道单粒子Green函数，多粒子的Green函数就可以计算出来.因此，只需求解单粒子Green函数.记n粒子Green函数为Gn.对于相互作用系统，G1的方程中会出现G2，G2的方程中会出现G3等.对于这样的一个方程链，必须引入截断才能处理.其中一种截断方式是集团展开［24－25］.现在就要将这样的方法应用于非平衡动理学方程.

为了方便和具体，用V－t2模型（紧束缚模型加上近邻相互作用）来表达一般理论.子系统定义为

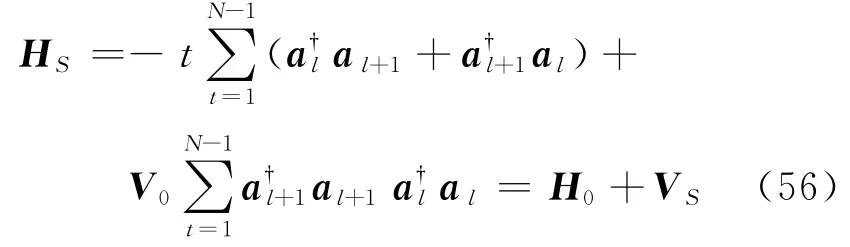
耦合到左右两端的两个热浴上，其Redfield方程可以按照式（16）写出.

同样，只对定态感兴趣ρ（∞），并且用这个定态来计算各种物理量.对于任何定义在子系统的物理量A，从定态Redfield方程（式（16）取左边等于零）得到A满足的方程

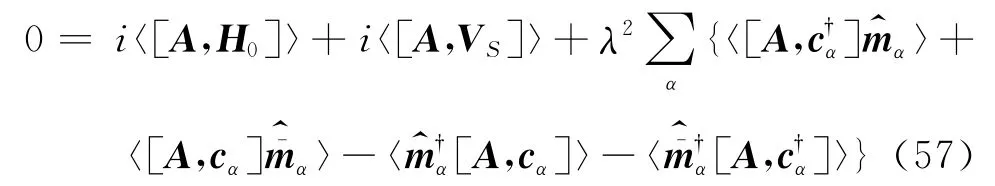
这是中心方程.其它方程都将从这个方程中推导出来.根据多体理论，任何物理量都可以表示成为产生湮灭算符的函数.如果知道了所有的各阶Green函数，就能够计算任何物理量.下面计算Green函数，从单粒子

和双粒子开始

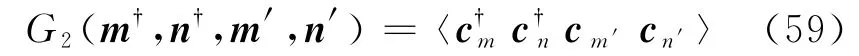
就像在平衡态BBGKY链与集团展开中一样，先从无相互作用的子系统开始.这就是令式（60）中V0＝0.发现这时热浴算符也只有产生湮灭算符的线性项.合起来，发现此时G1的方程是封闭的.还可以证明此时G2的方程与G1的方程等价，也就是说G2完全由G1给定.这正好就是平衡态Wick定理的内容

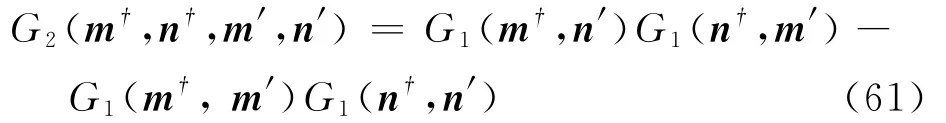
以它为基础，就可以来构造微扰展开.对于相互作用系统，方程右侧还有额外的项，记为

通常也称前者为Hartree－Fock项，后者为关联项.更高阶的Green函数也有类似的展开关系，加上额外的关联项［9，25］.集团展开的基本思想就是在某一级忽略这样的关联项.例如取G2＝0就得到了G1的封闭方程.这相当于是一级集团展开.还可以在G3中保留G1和G2而取G3＝0.这就相当于二级集团展开.同时对于相互作用系统，热浴算符也不仅仅包含产生湮灭算符的一阶项.通过微扰计算可以得到热浴算符的逐级展开形式，例如

其中，Dα；m与Dα；m1m2m3的定义请参见文献［8－9］.

把集团展开与热浴算符的展开形式代入G1的方程，可以得到G1的封闭方程.其主要部分是一个线性方程，同时包含非线性的微扰项.这样的方程可以通过迭代的方式求解.在小系统上，将用这一阶近似求得的近似解gC′，（1），不考虑相互作用的零阶近似求得的近似解gC′，（0）和数值精确解gEx作对此，分别计算了密度矩阵的距离与粒子流，见下页图7［8］.图7（a）和图7（b），展示了一阶解的距离dC，（1）和零阶解的dC，（0）随着ΔT和V0的变化，即dC，（1）都要比dC，（0）小很多.在图7（c）和图7（d）中，展示了JC，（0）和JC，（1）随着ΔT和V0的变化，并与数值精确解JEx做了比较.从图7（c）中可见，在相互作用比较小的时候（V0＝0.2），JC，（0）与JC，（1）都离JEx不远.在图7（d）中，看到当相互作用比较大时，JC，（1）要远远好于JC，（0）.由此可初步得出结论：在相互作用比较小的条件下，两种结果符合的很好；从零阶近似（也就是忽略相互作用）到一阶近似确实有很大的提高.用二阶近似作了同样的计算（计算结果还没有正式发表）.初步的处理可以在http：∥ccr.bnu.edu.cn／wujinshan上看到.其结果比一阶近似有了更大的提高.

图7 N＝4系统上类BBGKY一阶近似解gC，（1）和零阶解gC，（0）与精确数gEx对比图Fig.7 The first order approximation solution of BBGKY－like compared with the exact solution for interacting systems at non－equilibrium

4.3 量子随机微分方程方法

用确定性动理学方程描述系统是统计力学的一种思路，用随机过程表述系统是统计力学的另一种思路.现在将上面这个确定性动理学方程转化为随机微分方程，然后用Langevin方程、Monte Carlo模拟等方法来求解这样的方程定态.

将产生湮灭算法转化为导数算符，密度矩阵转化为密度分布函数的方法是利用相干态表象.在量子光学中，光子的量子主方程经常通过在相干态表象中转化为随机微分方程来求解［27］：密度矩阵成为“概率密度分布函数”（形式上，实际有时取负值），产生湮灭算符成为导数算符.在量子光学中所讨论的问题经常是动力学的或者是平衡态的.在这个意义上的工作就是将这样的技术推广到非平衡态的研究中去.

对于一个N格点系统，通过这样一个变换得到的随机微分方程有2N个复随机变量.下面以N格点Bose－Hubbard［28－29］为例简单介绍这个方法，得到的方程有时可以解析求解，有时要通过Monte Carlo模拟来求解随机微分方程对应的Langevin方程［27，30］.

相干态表象有很多种，这里只介绍其中的一种.一个常用的相干态表象是P表象［27］.在P表象下，第i个格点所对应的随机变量ξi和ξ＊i看成相互共轭的变量，因此，只考虑N个随机变量.对于很多系统，两者是要分开考虑的.一个关于各种不同表象的综述可以在文献［27，31］中找到.已有的研究表明这种技术可以处理约15×104个原子在106个动量本征态上的BEC动力学［32］.本文仅利用这种方法给出无相互作用系统的非平衡态的解析表达式，对于相互作用系统，数值工作还不很成熟.

为了讨论更具体，以双热浴中的一维Bose－Hubbard模型［28－29］为例，介绍相干态表象下的量子随机微分方程方法.左右热浴的温度分别为TL＝和子系统、热浴、耦合项分别定义为

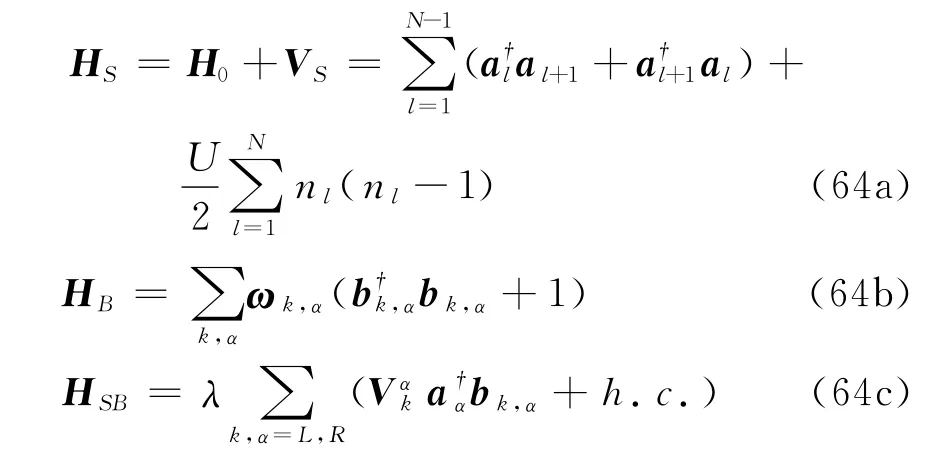
约化密度矩阵的Redfield方程为式（13）

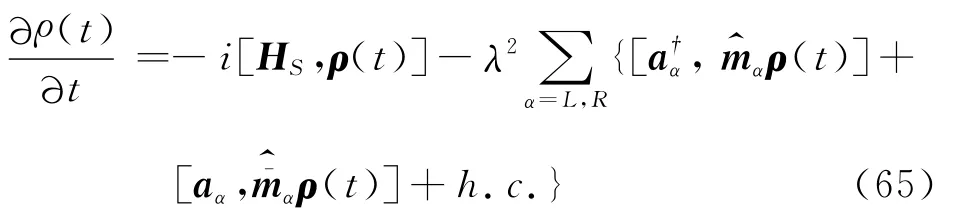
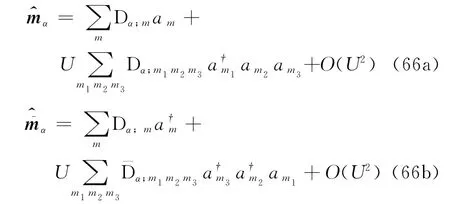
下一步，利用P表象，将a†l和al替换成导数算符，例如

这样就得到一个广义Fokker－Planck方程.对于无相互作用系统，这一方程退化成为标准Fokker－Planck方程［30］.在此，只给出这个无相互作用系统的方程.

其中，Z是归一化常数，矩阵σ是下述方程的解

图8为这个解析解与类BBGKY数值解的对比Green函数d和粒子流J，参数取N＝2，λ＝0.5，T＝2.0，μ＝－2.0，红色（蓝色）曲线是解析解（数值模拟）与类BBGKY数值解的对比，结果符合得较好.在考虑相互作用的系统中，必须通过数值模拟来求解广义Fokker－Planck方程.因此，在图8中，还将无相互作用系统的数值解与类BBGKY数值解做了对比，用来对数值方法做一个检验，也得到了符合较好的结果.

对于包含相互作用的中心系统，得到的广义Fokker－Planck方程在标准Fokker－Planck的基础上加入了高阶导数项.有的学者认为这样的广义Fokker－Planck方程仍然能够转化为广义Langevin方程求解［30，33］.而有的学者认为，必须发明新的方法或者想办法去掉这样的高阶导数项，例如通过使用Gaussian相空间的方法［31］或者把整体系统而不仅仅是中心系统的演化纳入考虑［34］.两者都有可能成功，尤其是后者，并认为可以得到更加可靠的结果，应该被更加广泛的应用；而且这样的处理能够很容易地求解非Markovian过程.目前，正在开展沿着这个思路的工作.

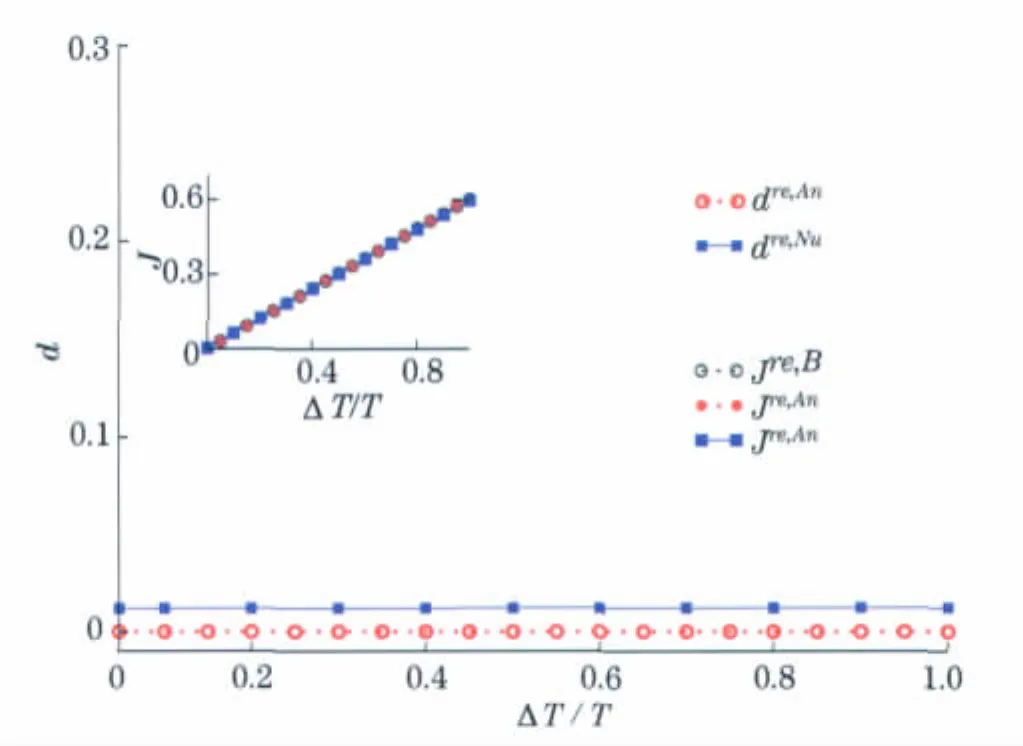
图8 无相互作用系统上相干态表象下非平衡态的精确解与类BBGKY数值解的对比Fig.8 Analytical solution compared against the BBGKY numerical solution

本文利用相干态表象找到了无相互作用系统的Redfield方程的解析解，对相互作用系统也大致阐述了求解的思路与技术.实际上，这一技术也能够用来处理Lindblad方程，而且更简单.还可以证明这一方法也能给出前面类BBGKY方法中的级联方程.但是，注意到完全发挥这一方法的威力还需要解决含有三阶导数项的广义Fokker－Planck方程的求解问题，这一问题还有待研究.

5 结论与展望

主要介绍处理量子系统非平衡定态的量子主方程方法的一般框架、计算技术，以及最新提出的两种技术.这两种技术不仅可以处理Redfield方程，也可以处理Lindblad方程等其它量子主方程.其方法不仅可以处理非平衡态也可以处理平衡态与动力学.在处理平衡态的时候，不需要从Boltzmann分布出发来计算，主方程演化的稳态自然就是Boltzmann分布.另外，相干态表象下量子随机微分方程的技术能够处理非常大的系统，有可能用来研究热浴和子系统构成的整体系统的动力学.这样，就可以研究统计物理学的第一个基本问题：热平衡分布的充分必要条件.可以让系统处于不同的初始状态，可以将二级微扰、Markovian近似、无限大热浴这些假设都去掉或者换成别的假设，来探讨子系统的演化末状态.

另外，统计物理学的第二个基本问题：系综分布与单一宏观系统的测量，也可以通过量子主方程与稳态分布的框架来讨论.前面提到，系统自身回复时间的尺度很大，通常大于宏观测量的时间尺度，因此长时平均等于系综平均的说法实际上不合理：系统在宏观测量下没时间作长时平均.实际上与宏观测量时间对比的不是系统自身的回复时间，而应该是系统在环境耦合下的回复时间.这样做的物理图景相当于宏观测量扰动了系统，使其偏离了平衡态（或者说得到了平衡态分布的一个抽样），接着环境迫使系统回复到平衡态，然后下一次宏观测量又扰动了系统，如此反复，直到宏观测量结束.所以，宏观测量在环境的帮助下，相当于给定分布函数的抽样过程，自然其平均等于概率平均，实际模型上的计算过程还在进行.

总之，这个一般框架加上计算方法不仅可以提供一个用来计算非平衡态的一般道路（统计物理学的第三个基本问题），还可以解决第二个基本问题，还有助于解决第一个基本问题.

本文首先从统计物理学本身对非平衡定态研究做了总结，现在再从系统科学的角度来看这个方向的意义.科学可以从研究对象来划分，也可以从研究深入的层次来划分为基础科学与应用科学，从研究内容上还可以分为研究处理研究对象方法的还是研究具体系统性质与规律的.整个物理学基本上是研究物理系统的学问，研究具体系统的性质和规律，同时也研究处理物理系统的方法.具体到统计物理学，它更多地研究处理相互作用的多体系统的处理方法，当然，也研究典型物理系统、典型物理模型.系统科学研究更加一般的（物理的或者非物理的）系统的处理方法.系统科学没有特定的研究对象，它关注的具体学科领域有很多，包括经济、工程、社会、物理、地理、生物、心理等各个领域.也许从研究对象来看它是一门交叉科学，但是系统科学是方法论性的学科，不是以研究对象来安身立命的学科.从这个意义上说，它不是交叉科学，仅仅是研究对象交叉起来的科学，其研究方法（至少希望）是一致的统一的，成系统的，有内在逻辑关系的.它从具体的学科来，到一般的方法中去，然后再从一般的方法到具体的学科中去.也许前后这两个具体的系统属于不同的学科或者同一个学科.系统科学注重事物（来源于相同或者不同学科的具体系统）之间的联系，发现其共同与不同的地方，借鉴和发展某一具体系统的研究与处理方法，应用于解决另一具体系统的问题.在这里，关键词就是：联系、共同点、方法、解决问题.尤其是联系，这意味着从事物之间，或者事物内的部分之间的联系，也就是从相互作用出发，来考虑问题.这是系统科学非常重要的考虑问题的角度，有时候称它为“系统的思想”.有的人把它称为整体与部分，用整体的观点来考虑问题，这也有一定道理.但是，也应尽量避免这个提法，因为这看起来好像部分的研究不重要了，整体才是重要的，更好的理解方式应该是说，部分的研究是不能完整地描述整体的，还需要从整体来考虑，有的时候相互作用系统的整体行为与系统的个体的直接行为之间是有差别的，这也被称为涌现性问题.由于系统科学主要关注相互作用（有时候甚至是多种相互作用的混合）的多体系统，并考察多个层次上的涌现性问题，在这个意义上系统科学也常常被称为复杂性研究.

对于系统科学这样一个研究方法，解决多个具体系统的问题的一门学问，它的主要方法又从哪里来，物理学是研究所有自然现象最基础的学科，它既研究具体系统，也研究方法.物理学探讨对自然现象的描述，进而研究现象出现和演化的推动力来理解现象，或者有的时候还要预测和控制现象.物理学的精神就是：寻找和发现客观现实，探寻其原由，以至（希望）所有自然现象都能够用最简单的统一的方式来描述和理解.物理学的发展扩大了其研究对象，一方面，物理学的方法，尤其是统计物理学的方法，还被应用于社会现象的研究，而不仅局限于自然现象.当然，这还没有成为物理学的主流.物理学这种很强的侵略性使得一部分研究非物理系统的学者对其爱恨交加，也使得最传统的物理学研究者恨爱交加.另一方面物理学对复杂系统的研究使得某些研究问题和某些研究方法，开始从最传统的物理学稍微地分离开来.例如，统计物理学和热力学展示物理系统通常具有趋向热平衡的特性，可是结构和花样的出现也是一个普遍事实，例如Poiseuille－Bernard流中花样的形成、Belousov－Zhabotinsky反应中花样的出现，甚至生物的进化.在一定条件下，系统可以从各项同性的没有结构的状态演化成有结构的状态.这些问题的研究有其自身的共性，虽然还可以看作是物理学、化学或者生物学的研究，但是把它们联合起来从原来的学科中独立出来还是有意义的.这也促使系统科学的研究从传统物理学中区别开来.

这样的现象尽管主要出现在物理学研究中，在其它学科，例如生物学、生态学、经济学、社会学中也有类似风格的工作：发展和利用其它学科或者本学科的方法，寻找不同具体系统之间的共性和差异，然后解决本学科或者其它学科的问题.所以，系统科学方法的一个重要来源就是物理学，尤其是统计物理学.当然，广义上说，数学本身就是这样一门学问：从实际问题中（主动地或者被动地）提炼出抽象结构，研究和发展这样的结构，然后用于实际问题的研究.从这个意义上，系统科学也可以看成是数学的一个分支学科.不过，能看成数学分支的学科太多了，例如理论物理学、理论生物学等，这些都是广义的数学模型方面的学科.因此，把系统科学独立出来看，还是有一定意义的.

系统科学就是在这样的一个背景下得到了比较大的发展：类似风格的研究者和研究工作聚集在一起，用“系统的思想”来研究一个或多个具体系统.基于这样的特征，人们给这些人和工作取了个名字：系统科学.而且发现这样一个处理相互作用的多体系统的思想与方法与统计物理学是紧密结合的.因此，希望这个关于统计物理学基本问题研究的综述不仅仅对物理学工作者有意义，还能够帮助系统科学的研究者建立一个粗略的图景.大量来自于平衡态统计物理学的模型与方法，例如Ising模型、相变与临界现象理论、动力学系统的行为与底层几何结构的关系、有限大小标度、系综理论、Metropolis模拟方法及Green函数方法等，已经进入了系统科学的研究.可以预见，在不久的将来，非平衡态的模型与方法，包括处理非平衡系统的一般框架、处理相互作用的Green函数方法与集团展开方法、量子随机方程的技术等等，也将成为系统理论基础的一部分.

［1］ Goldstein S，Lebowitz J L，Tumulka R，et al.Canonical typicality［J］.Physical Review Letters，2006，96（5）：050403.

［2］ Dubey S，Silvestri L，Finn J，et al.The approach to typicality in many－body quantum systems［J］.Phys Rev E，2011，85（1）：011141.

［3］ Singh N.How and why does statistical mechanics work［EB／OL］.［2011－03－21］.http：∥arxiv.org／abs／1103.4003.

［4］ Linden N，Popescu S，Short A J，et al.Quantum mechanical evolution towards thermal equilibrium［J］.Phys Rev E，2009，79（6）：061103.

［5］ Saito K，Takesue S，Miyashita S.Energy transport in the integrable system in contact with various types of phonon reservoirs［J］.Physical Review E，2000，61（3）：2397－2409.

［6］ Prosen T，Znidaric M.Matrix product simulations of non－equilibrium steady states of quantum spin chains［J］.Journal of Statistical Mechanics：Theory and Experiment，2009，2009：p02035.

［7］ Wichterich H，Henrich M J，Breuer H P，et al.Modeling heat transport through completely positive maps［J］.Physical Review E，2007，76（3）：031115.

［8］ Wu J.Non－equilibrium stationary states from the equation of motion of open systems［J］.New Journal of Physics，2010，12（8）：083042.

［9］ Wu J.Quantum transport through open systems［D］.Vancouver：The University of British Columbia，2011：79－96.

［10］ Lepri S，Livi R，Politi A.Thermal conduction in classical low－dimensional lattices［J］.Physics Reports－Review Section of Physics Letters，2003，377（1）：1－80.

［11］ Landauer R.Electrical resistance of disordered onedimensional lattices［J］.Philosophical Magazine，1970，21（172）：863－867.

［12］ Cresti A，Farchioni R，Grosso G，et al.Keldysh－green function formalism for current profiles in mesoscopic systems［J］.Physical Review B，2003，68（7）：075306.

［13］ Kubo R.Statistical－mechanical theory of irreversible processes 1：general theory and simple applications to magnetic and conduction problems［J］.Journal of the Physical Society of Japan，1957，12（6）：570－586.

［14］ Wu J，Berciu M.Kubo formula for open finite－size systems［J］.Europhysics Letters，2010，92（3）：30003.

［15］ Toher C，Filippetti A，Sanvito S，et al.Self－interaction errors in density－functional calculations of electronic transport［J］.Phys Rev lett，2005，95（14）：146402.

［16］ Evers F，Weigend F，Koentopp M.Conductance of molecular wires and transport calculations based on density－functional theory［J］.Phys Rev B，2004，69（23）：235411.

［17］ Kubo R，Toda M，Hashitsume N.Statistical physics II：nonequilib－rium statistical mechanics［M］.Berlin：Springer，1991.

［18］ Blum K.Density matrix theory and applications：physics of atoms and molecules［M］.New York：Springer，1996.

［19］ Redfield A G.On the theory of relaxation processes［J］.IBM Journal of Research and Development，1957，1（1）：19－31.

［20］ Redfield A G.The theory of relaxation processes［J］.Adv Magn Reson，1965，1：1－32.

［21］ Kondov I，Kleinekathofer U，Schreiber M.Efficiency of different numerical methods for solving redfield equations［J］.Journal of Chemical Physics，2001，114（4）：1497－1504.

［22］ Mahan G D.Many－particle physics［M］.New York：Plenum Press，1990.

［23］ Petrina D Y.Mathematical foundations of quantum statistical mechanics［M］.Dutch：Kluwer Acad Publ，1995.

［24］ Kadano L P，Martin P C.Theory of many－particle systems II：superconductivity［J］.Physical Review，1961，124（3）：670－697.

［25］ Kira M，Koch S W.Many－body correlations and excitonic effects in semiconductor spectroscopy［J］.Progress in Quantum Electronics，2006，30（5）：155－296.

［26］ Martin P C，Schwinger J.Theory of many－particle systemsi［J］.Physical Review，1959，115（6）：1342－1373.

［27］ Gardiner C W，Zoller P.Quantum noise［M］.Berlin：Springer，2000.

［28］ Jaksch D，Bruder C，Cirac J I，et al.Cold bosonic atoms in optical lattices［J］.Physical Review Letters，1998，81（15）：3108－3111.

［29］ Greiner M，Mandel O，Esslinger T，et al.Quantum phase transition from a superfluid to a mott insulator in agas of ultracold atoms［J］.Nature，2002，415（6867）：39－44.

［30］ Risken H.The Fokker－planck equation：methods of solutions and appli－cations［M］.Berlin：Springer，1989.

［31］ Drummond P D，Deuar P，Corney J F.Quantum many－body simula tions using gaussian phase－space representations［J］.Optics and Spectroscopy，2007，103（1）：7－16.

［32］ Deuar P，Drummond PD.Correlations in a bec collision：first－principles quantum dynamics with 150 000atoms［J］.Physical Review Letters，2007，98（12）：120402.

［33］ Plimak L I，Olsen M K，Fleischhauer M，et al.Beyond the fokker－planck equation：stochastic simulation of complete wigner representation for the optical parametric oscillator［J］.Europhysics Letters，2001，56（3）：372－378.

［34］ Palmieri B，Nagata Y，Mukamel S.Phase－space algorithm for simulating quantum nonlinear response functions of bosons using stochastic classical trajectories［J］.Physical Review E，2010，82（4）：046706.