一种对GPS/INS组合导航的曳引式拉偏干扰

陈 军，王义冬，刘 义，王大明

（1．北京航空航天大学，北京 100191；2．63880 部队，河南 洛阳 471003；3．91872 部队，北京 102442）

数据融合技术将全球卫星导航系统(Global Positioning System，GPS)和惯性导航系统(Inertial Navigation System，INS)紧密结合起来[1]，GPS/INS组合导航已在航空和军用飞机上被广泛应用。在GPS/INS 组合导航中，通过GPS 信息与INS 信息的数据融合，大大提高了导航系统的抗干扰性，传统的对抗措施已难以起效，寻找对GPS/INS 组合导航有效的干扰方法，已成为导航对抗领域的研究难点。

关于GPS/INS 组合导航的相关研究，主要集中在组合导航的算法及性能分析[2-8]，而对对抗方法研究相关成果很少[9-10]。本文在总结GPS/INS 组合导航原理及抗干扰性能的基础上，提出曳引式拉偏干扰，给出干扰的定义、数学表达形式、简化形式，通过半实物仿真实验证明其有效性并对其干扰效果进行分析。

1 GPS/INS 抗干扰性能分析

利用GPS/INS 组合导航中INS 提供的信息，可以增强GPS 信号的抗干扰能力，表现为以下几个方面：可以利用INS 信息剔除由于对抗活动(诱骗干扰)造成的GPS 测量值异常；当机动、干扰或遮挡使GPS 信号丢失时，惯导可以辅助GPS 重新捕获GPS信号；可使GPS 接收机跟踪环路的带宽取得很窄，解决了动态与干扰的矛盾。

如图1 所示，在松耦合组合导航中利用GPS 量测信息对惯导误差进行修正时，首先要判断GPS 输出数据是否为异常值。由于惯导的短时误差的高精度，短时间内得到位置估值准确性高，可以作为GPS量测数据是否异常的判断依据。对于获得的GPS 数据，首先对其进行是否异常判断，如果GPS 的量测数据为异常值将舍弃，不是异常值，则作为量测值输入GPS/INS 融合算法。

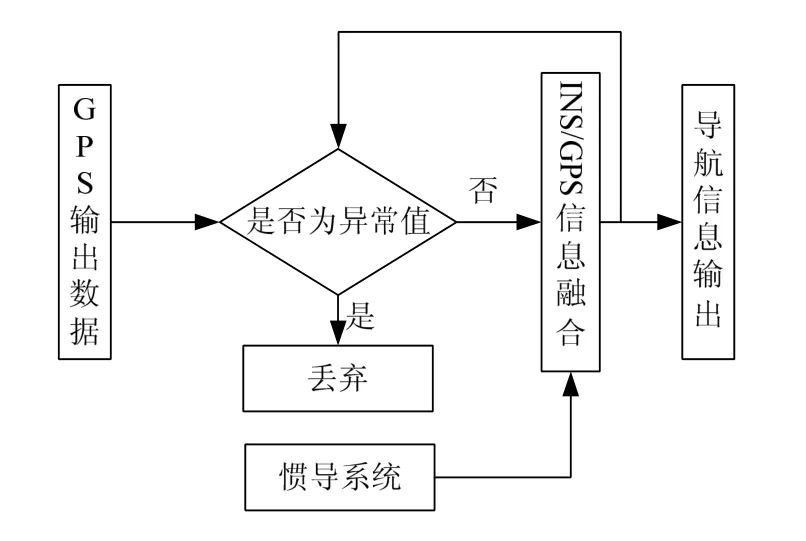
图1 GPS/INS 数据处理流程图

下面我们对GPS 数据异常与否的判断方法进行讨论。根据传统概率数理统计计算方法，应用3δ法则进行误差值剔。当GPS 定位值ZGPS满足

时，认为其为异常值。

式(1)中，δins-gps由惯导误差与GPS 测量误差决定，在惯导误差与GPS 量测误差均为加性误差，且GPS 量测误差为零均值时有：

式(2)中：δgps为GPS 的量测误差标准差；δins为惯导系统定位误差标准差，其大小由惯导设备决定。目前的微惯导器件的精度为：0.1～1(°)/h精度的微陀螺、1～10 mg 精度的微加速度计。已知GPS/INSr融合周期为2 s，δins的大小约在4～40 m。

2 对GPS/INS 组合导航的曳引式拉偏干扰

2.1 曳引式拉偏干扰的定义及工作原理

定义：通过干扰设备产生欺骗干扰信号，使GPS/INS 组合中的GPS 接收机输出与其实际位置逐渐偏离的导航定位数据，当偏离误差ΔZGPS满足时，称这种干扰信号为“曳引式拉偏”干扰。式(3)中，δins-gps由惯导误差与GPS 测量误差决定。

GPS 导航定位的基础就是测距，即通过测量时差获得卫星和接收机之间的伪距。之所以称为伪距，是由于卫星钟和用户钟之间的钟差存在，测得的距离并非真实距离，而是包含钟差影响的距离。

伪距ρ′与卫星坐标(SVxi,SVyi,SVzi)、接收机坐标(Rx,Ry,Rz)之间有如下关系：

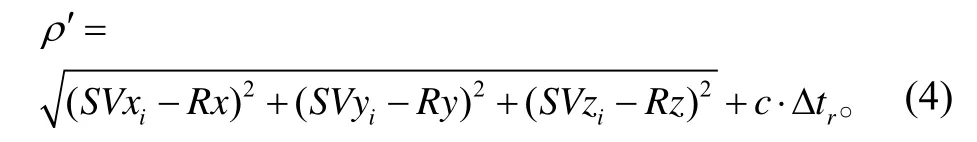
获得伪距后，即可解算定位结果：

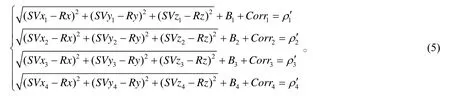
式(5)中：卫星坐标(SVxi,SVyi,SVzi)可由卫星导航电文数据计算求得；B为接收机钟差等效距离偏差(=c⋅Δtr)；Corri为第i颗卫星的已知修正量；ρi′为对第i颗卫星的观测伪距；接收机坐标(Rx,Ry,Rz)和接收机钟差rtΔ 为未知量，通过对式(4)解算求得。

为了产生“曳引式拉偏”干扰的效果，需要利用生成的干扰信号使通过相干接收及相应计算得到的伪距iρ′发生错误，根据错误的伪距iρ′进行定位计算，得到的定位结果与真实位置的误差满足式(3)。具体方法可以通过更改信号的时延(对应真星信号的时延)、频率(这里指多普勒效应带来的频差)来达到。

2.2 曳引式拉偏干扰的信号形式

假设某颗真星到达接收机的信号为

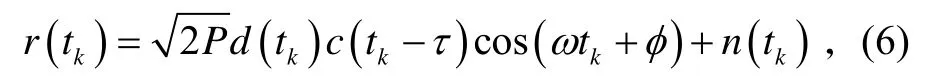
式中：P为信号功率；d(tk)为调制数据信息；c(tk−τ)为伪随机码序列；ω、φ分别为输入信号的角频率及相位；n(tk)为加性高斯白噪声。

则要求“曳引式拉偏”干扰生成的信号到达接收机时应为

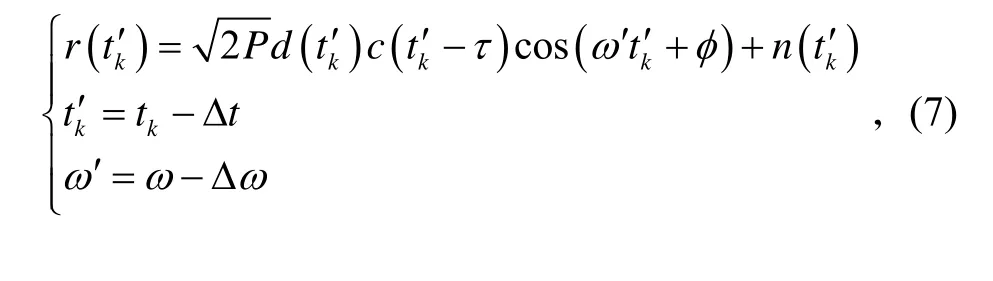
考虑到干扰设备与被干扰接收机之间的位置关系，干扰机发出的欺骗信号为

2.3 曳引式拉偏干扰的简化形式

通过前面讨论可知，要想获得“曳引式拉偏”的效果，理论上需要对干扰信号的延时、频率进行精确控制。为了达到这个目的，需要精确已知干扰目标的位置、当前时刻的星历、GPS 信号的形式，然后通过式(3)～(9)计算出干扰信号的时延与多普勒频率，生成欺骗干扰信号。由于接收机可以同时收到多颗星的信号，因而理论上需要产生多颗星的欺骗干扰信号。在实际应用，这样的要求十分苛刻，工程化的可能性不高。

但是实际上，获得“曳引式拉偏”的效果不需要如此苛刻的条件，由于GPS 接收机是根据多颗星的伪距来进行定位计算的，如果能够对一颗关键星的信号进行欺骗式干扰，也能达到部分“曳引式拉偏”干扰的效果(在后面的半实物仿真试验中将会证明)。

“曳引式拉偏”干扰的简化方式，只需要估算出目标的飞行轨迹，设定欲干扰阵地，利用干扰设备产生单星的欺骗干扰信号，使与干扰轨迹与目标飞行轨迹相交。

3 仿真实验

为验证所提干扰的有效性，利用一台GPS 信号模拟器(模拟器1)模拟蓝方来袭巡航导弹，速度约为50 m/s(180 km/h)，另一台模拟器(模拟器2)模拟红方防御的GPS 干扰信号，这个信号是横向运动的，速度设置为20 m/s 和50 m/s。模拟实验配置设备连接图如图2 所示。模拟器1 发出信号为−116 dBm，模拟器2 发出信号为−111 dBm，即干信比为5dB。

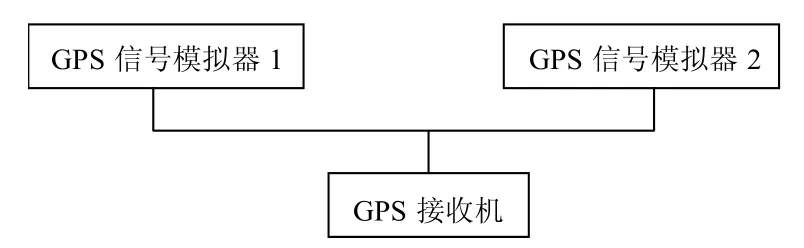
图2 “曳引式拉偏”干扰模拟实验配置

预设弹道为：起始位置为北纬0 度10 分，东经0 度0 分，以50 m/s 的速度向南飞行，飞行高度为200 m。模拟器时间设置为2012年12月2日12 点，可见卫星如图3 所示，预设轨迹如图4 所示。

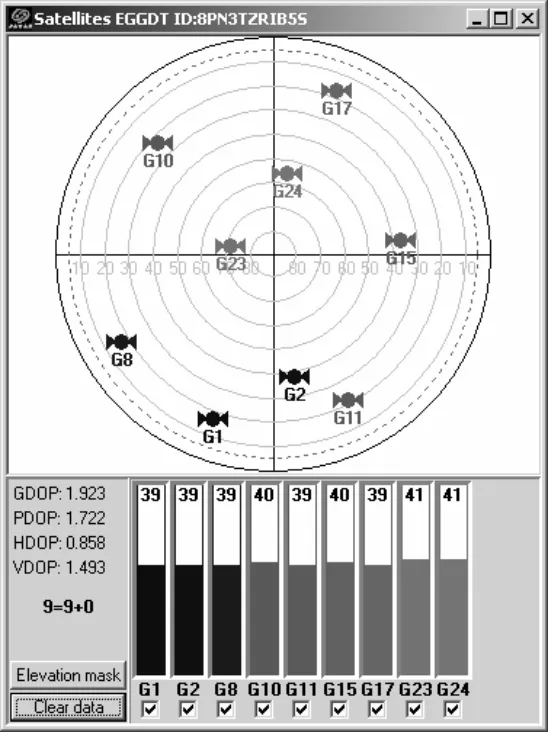
图3 “曳引式拉偏”干扰模拟实验设定星图

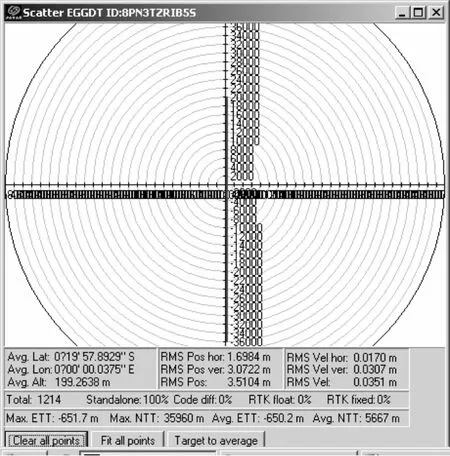
图4 “曳引式拉偏”干扰模拟实验预设弹道轨迹

干扰为“20 m/s 的速度在长度为1 km 的跑道形航线上往返飞行”，只发射单星的欺骗干扰信号，轨迹图如图5 所示。干扰为“50 m/s 的速度在长度为5 km 的跑道形航线上往返飞行”，只发射单星的欺骗干扰信号，轨迹图如图6 所示。

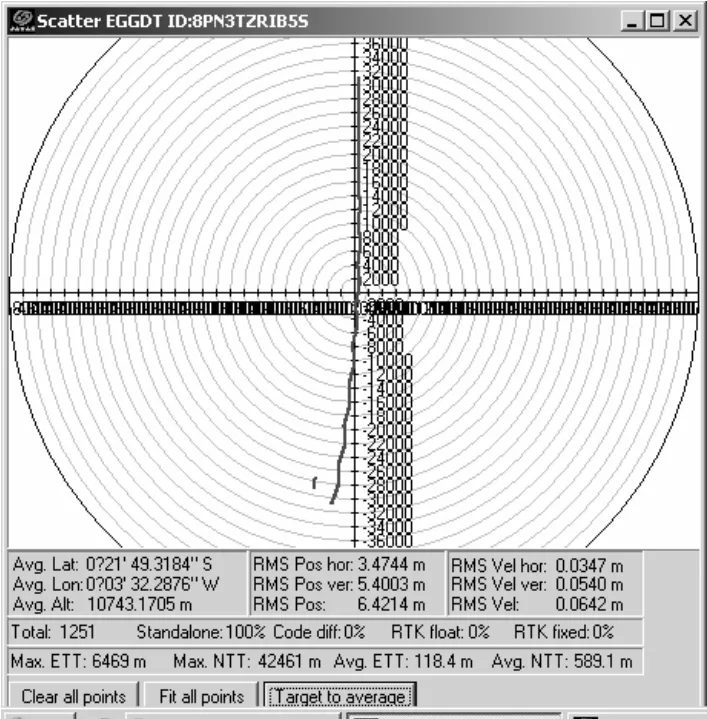
图5 “曳引式拉偏”干扰模拟试验结果1

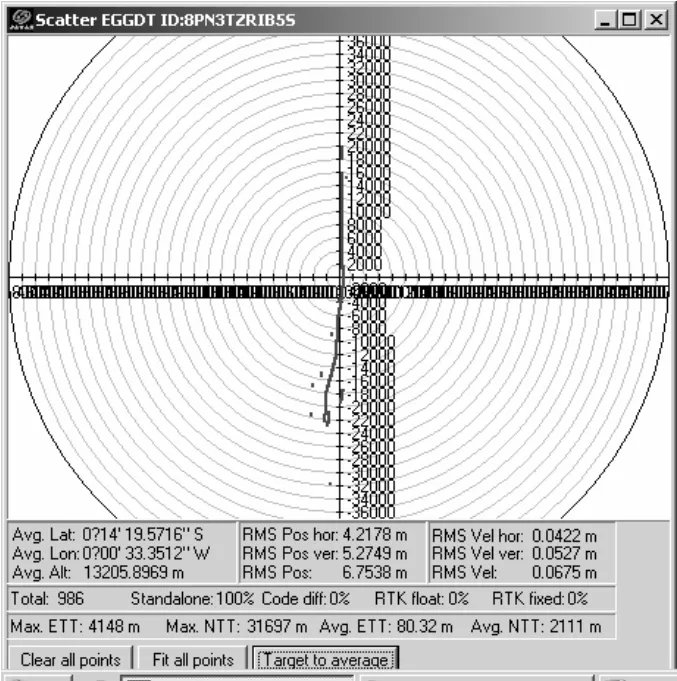
图6 “曳引式拉偏”干扰模拟试验结果2

对仿真结果进行分析可以发现，当目标位进入攻击阵地时正常飞行，进入攻击阵地后，发生“曳引式拉偏”现象。再具体比较图5 与图6，可以发现欺骗干扰的轨迹与其飞行轨迹之间的差别大小影响干扰效果，差别越小干扰效果越好。

4 曳引式拉偏对GPS/INS 组合导航的影响分析

为进一步对所提干扰方法效果进行分析，设计仿真试验进行验证。假设INS 的陀螺漂移的标准差与加速度计精度分为3 个档次：0.1 (°)/h，1 mg；0.5 (°)/h，5 mg；1 (°)/h，10 mg。GPS 接收机的数据刷新率为10 Hz，位置、速度误差分别为30 m、0.3 m/s，利用GPS 数据修正INS 的周期为2s。图7为利用不同精度INS 与利用GPS/INS 进行导航的定位误差时间的变化关系。可见只采用INS 进行导航时，导航误差随时间累积，误差变化率与INS 精度密切相关，INS 精度越高、误差变化率越小。而采用组合制导方式，导航误差不随时间累积，大大提高了定位导航精度。

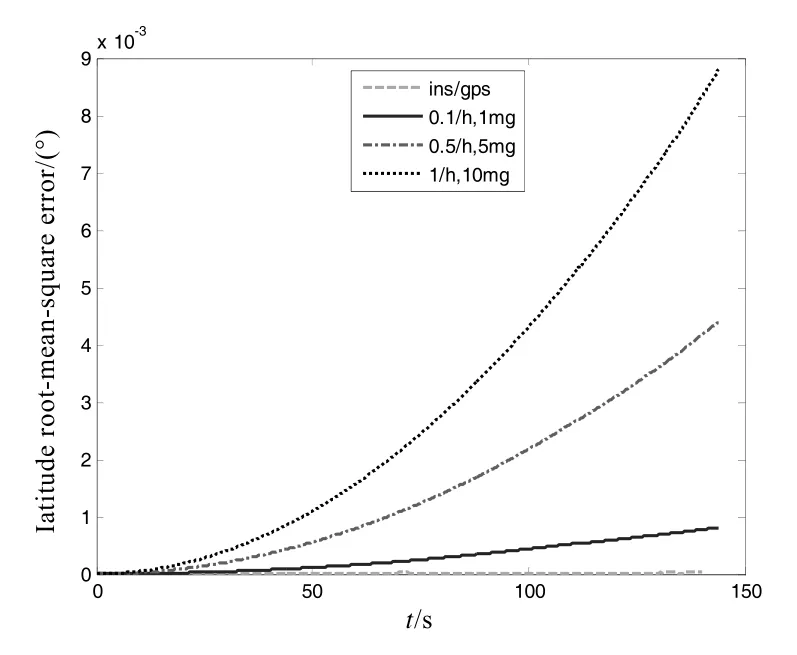
图7 典型弹道下导航定位误差比较

当GPS 受欺骗式干扰时，其输出数据发生变化。如果变化速度缓慢，在组合制导工作流程中无法利用式(1)将其剔除。这时导航信息会依据错误GPS 定位信息对惯导系统提供修正，最终使组合导航系统输出导航信息误差发生偏差。

假设GPS 受到欺骗干扰，使其北向、东向速度虚假增加了1 m/s 的速度。由于GPS 数据修正INS的周期为2 s，在上面假设的惯导误差下δins约在4～40 m，而由于欺骗干扰带来的GPS 定位误差约为3 m，无法利用式(1)将其剔除。图8 为典型弹道下组合导航受干扰与未受干扰定位误差比较。通过仿真分析可以看到，欺骗干扰可以影响组合制导的性能，能够使制导航线偏离规划弹道。

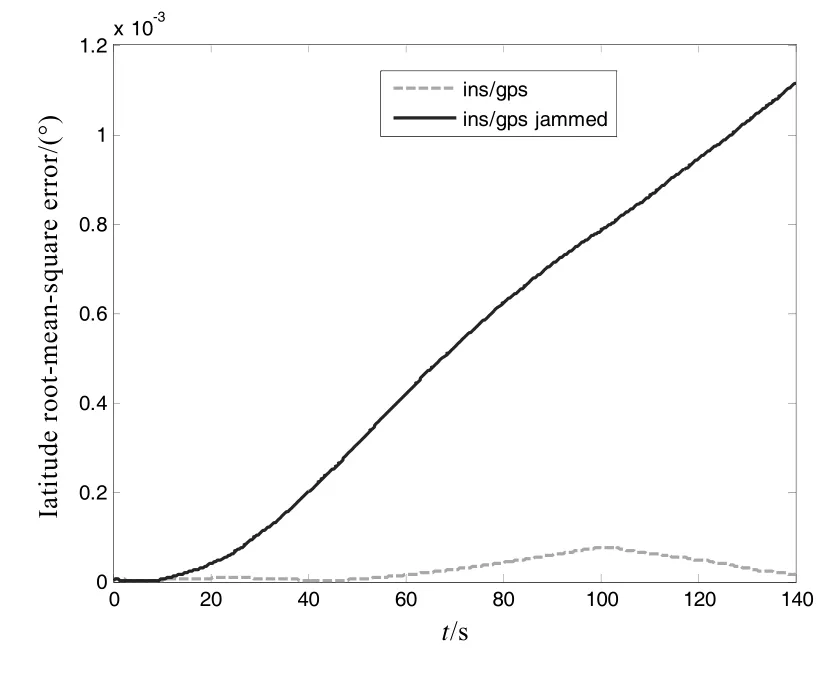
图8 欺骗干扰对组合制导的影响

5 结束语

本文首先对GPS/INS 组合导航的原理及其抗干扰能力进行分析，通过理论分析、计算机仿真实验、半实物仿真实验等方法论证了对GPS/INS 组合制导干扰的可行性。特别提出曳引式拉偏干扰方法，给出其定义、信号形式，分析其工程实现可行性，并通过半实物仿真实验证明其有效性并对其干扰效果进行分析。

[1] MOHINDER S GREWAL, LAWRENCE R WEILL, ANGUS P ANDREWS. Global positioning systems, inertial navigation, and integration[M]. 2nd ed. Hoboken∶ John Wiley & Sons. Inc., 2007∶234-254.

[2] 陈有荣, 袁建平. 一种改进的INS/GPS 组合导航鲁棒H∞多重渐消容错滤波算法[J].宇航学报, 2009,30(3)∶ 930-936.

[3] 王垚, 蔚保国, 罗显志, 等. 一种更精确的多模GNSS 兼容性方法研究[J]. 系统工程与电子技术, 2010,32(6)∶1305-1308.

[4] 王新国, 李爱华, 许化龙. 数据融合技术在 SINS/ CNS/GPS 复合制导中的应用[J]. 系统仿真学报, 2009, 21(10)∶3062-3066.

[5] 刘义. 对抗条件下被动雷达制导技术及效能评估方法研究[D]. 长沙∶ 国防科技大学, 2010.

[6] CRASSIDIS J L. Sigma-point kalman filtering for integrated GPS and inertial navigation[J]. IEEE Trans. on AES, 2006,42(2)∶750-756.

[7] 林雪原, 鞠建波. 利用神经网络预测的GPS/SINS 组合导航系统算法研究[J]. 武汉大学学报∶ 信息科学版, 2011,36(5)∶601-604.

[8] 窦长江. 卫星导航用户机自适应滤波研究[J]. 无线电通信技术, 2006(6)∶48-50.

[9] 路远, 陈鹏举. 对GPS/INS 制导巡航导弹的干扰研究[J]. 航天电子对抗, 2003,19(1)∶6-9.

[10] 周坤芳, 李德武, 周湘蓉. 干扰环境下GPS/INS 组合模式研究[J]. 中国惯性技术学报, 2004,12(4)∶24- 27.