考虑轴向力及附加质量的谐振音叉建模及仿真

郭占社， 宋春苗， 郑仕学

（1. 北京航空航天大学仪器科学与光电工程学院，北京 100191；2. 重庆嘉陵华光光电科技有限公司，重庆 400700）

谐振式MEMS传感器由于具有输出谐振频率信号，易于实现与计算机的数字接口且在传输时不易失真，已成为MEMS领域重要的研究方向。目前很大部分MEMS谐振式传感器都是通过检测内部谐振敏感元件的谐振频率微小变化量来实现对被测量的检测，因而谐振敏感元件的性能直接影响整个微系统的测试精度及应用场合[1-2]。

在该研究方面，传统的研究一般基于纯音叉梁形式。天津大学钟莹等分析了纯音叉谐振器的振动特性和工作原理并把它应用于加速度传感器；重庆大学刘恒[3-4]等根据双端固定音叉谐振器的动力学原理，建立参数模型，研究了音叉梁长度及宽度对谐振频率的影响；南京理工大学裘安萍[5]等通过研究指出音叉谐振器结构中振梁宽度产生的加工误差最大，且对谐振器的性能影响最大，而实际应用的音叉梁上均集成有驱动单元和检测单元，不可避免引入附加质量，施加附加质量后谐振梁振动模型具有较大改变，不考虑的话会引入很大误差。而且实际应用中是通过施加轴向力前后音叉梁谐振频率的变化来解算轴向力及所携带参数的大小，所以必须考虑携带附加质量的谐振梁受轴向力的振动问题，这种振动问题在音叉谐振器微结构的建模和设计中频繁用到[6-8]，谐振频率作为设计和操作参数的函数，它的确定需要准确的模型。但是，目前综合考虑附加质量与轴向力对音叉振动特性的影响的相关文献很少。

本文充分考虑了附加质量与轴向力对谐振音叉振动特性的影响，建立携带附加质量的谐振梁的振动模型，采用有限元方法对其进行仿真，并对其重要性进行研究。

1 谐振音叉工作原理分析

双端固定音叉结构简图如图1所示，该结构主要由两根平行的谐振梁组成，梁的末端连接在一起，并与支撑结构相连。当通过适当的激励方式使两个音叉臂平面内反相振动时，两个音叉臂在它们的合并区域产生的应力和力矩方向相反，互相抵消，因此整个结构通过固定连接端与外界的能量耦合小，振动系统的能量损失小，具有很高的Q值。

图1 双端固定音叉

音叉谐振器结构简单，具有力平衡、自减震的特性，在微系统中用作力的敏感元件或转换元件，一般工作在闭环自激的谐振状态，通过它的谐振频率变化解算出轴向力从而获得所携带的参数。

2 考虑轴向力和附加质量模型

谐振音叉主要用于敏感施加轴向力后传感器谐振频率的变化，谐振音叉的性能直接决定了整个传感器的性能，目前的研究是基于纯谐振梁的振动特性进行的，而实际情况在谐振梁上集成了驱动单元和检测单元等，该部分可等效于具有一定质量的附加质量。当谐振音叉存在轴向力和附加质量块的影响时，其振动模型会发生很大的改变。本文针对该问题，建立如图2所示具有附加质量的音叉谐振梁的振动模型。

图2 具有附加质量的谐振音叉模型

2.1 纯音叉梁模型

应用瑞利法和能量守恒定律可得

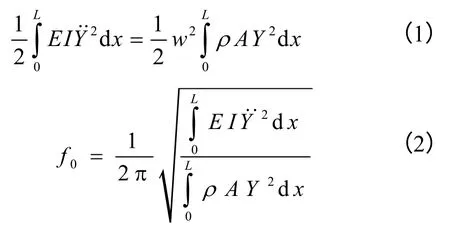
通过数值拟合取振型函数[9]

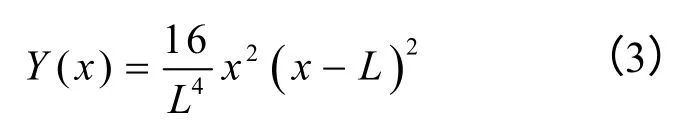
其中Y(x)为梁振动的模态函数，L为梁长，f0为纯音叉梁不受轴向力时的谐振频率，ρ为梁的密度，A为梁的截面积，EI为梁的抗弯刚度。

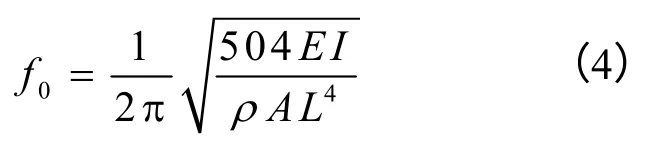
2.2 携带附加质量的音叉梁模型

携带附加质量块时，在梁的振动过程中，梁的动能既包括梁的动能，又包括梁上附加质量块的动能。

应用瑞利法和能量守恒定律可得

其中s为附加质量块距梁端部的距离，ma为附加质量块的质量。

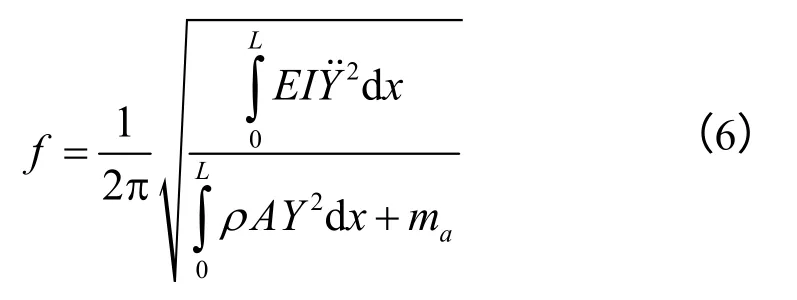
结合振型函数式(3)

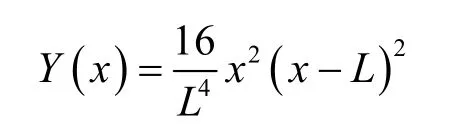
则

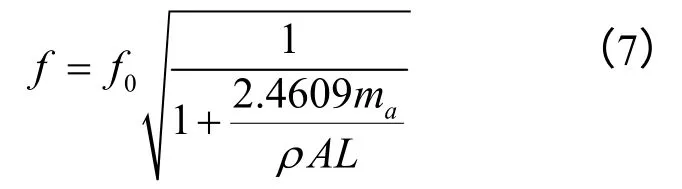
利用Matlab软件，得到附加质量与谐振频率之间的关系如图3所示。

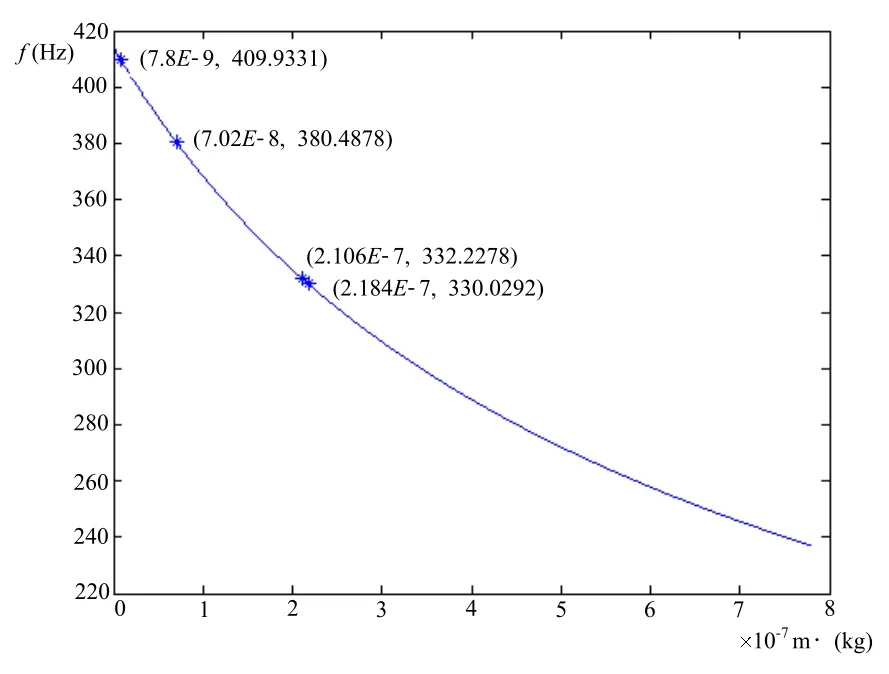
图3 无轴向力时谐振频率随附加质量的变化趋势

当附加质量远小于音叉梁的质量(ma＜＜ρ*A*L)

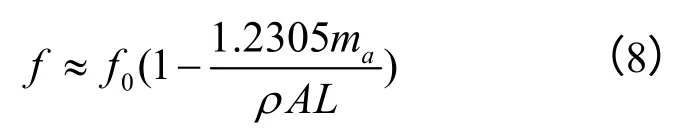
2.3 存在轴向力的音叉梁模型

轴向力存在时，在梁的振动过程中，梁的弹性势能中除了弯曲应变能之外，还包括轴向拉力引起的应变能，这部分势能在数值上等于轴向力在轴向位移上所作的功。

应用瑞利法和能量守恒定律可得

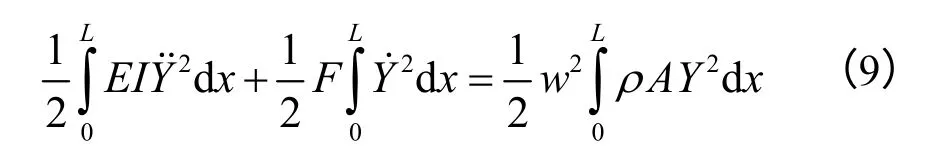
其中F为所施加的轴向力。

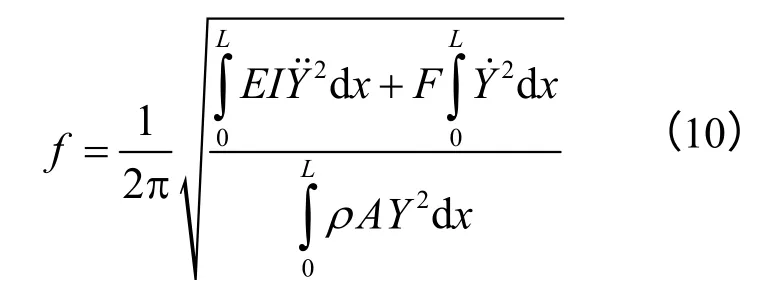
结合振型函数式(3)

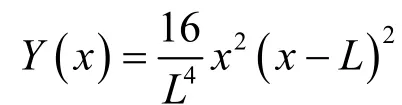
则

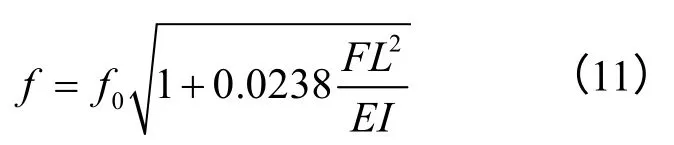
同样，得到两者之间关系如图4所示。

图4 无附加质量时谐振频率随轴向力变化趋势

当所施加轴向力很小时

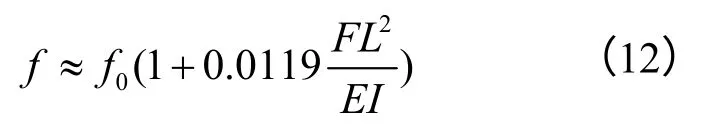
2.4 携带附加质量且存在轴向力的音叉梁模型

同时存在轴向力及附加质量块时，在梁的振动过程中，梁的弹性势能中除了弯曲应变能之外，还包括轴向拉力引起的应变能，这部分势能在数值上等于轴向力在轴向位移上所作的功，梁的动能则既包括梁的动能，又包括梁上附加质量块的动能。

应用瑞利法和能量守恒定律可得

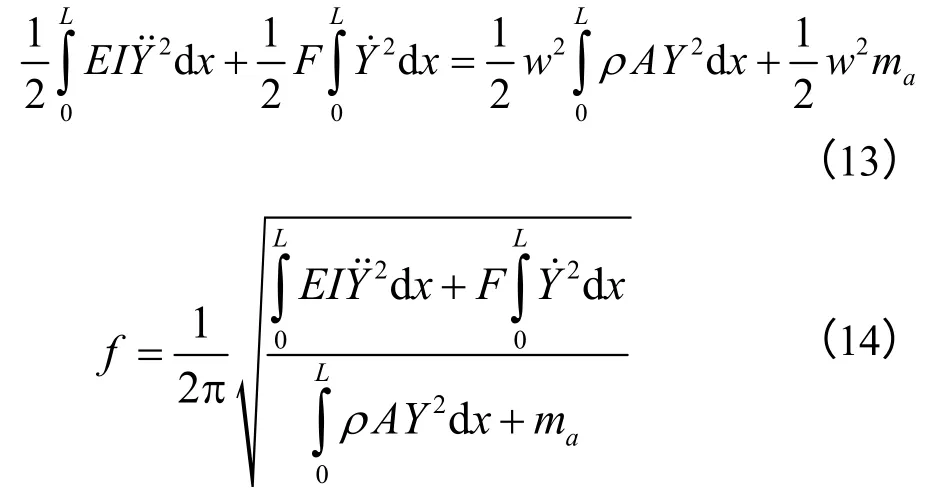
结合振型函数式(3)

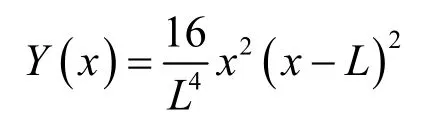
则

当附加质量远小于音叉梁的质量(ma＜＜ρ*A*L)，且所施加轴向力很小时

同样，利用Matlab软件，得到轴向力与谐振频率之间变化关系曲线如图5所示。

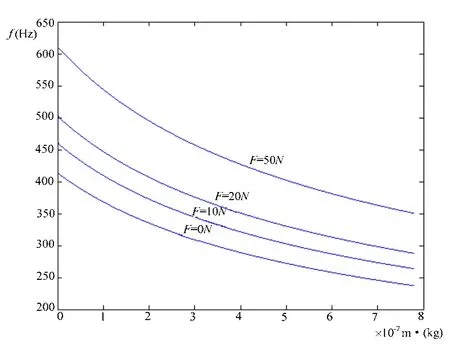
图5 有轴向力的谐振频率随附加质量变化趋势

3 有限元仿真

为验证理论的正确性，我们建立有限元模型如图6所示，取 E=2.06*105MPa，ρ=7.8*10-9kg/mm3，A=a*b，I=a*b3（a为梁高，b为梁宽），a=3mm，b=0.5mm。

F=0时，即无轴向力，则同式(7)

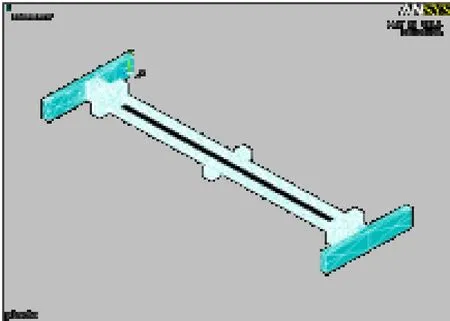
图6 有附加质量的音叉梁有限元仿真

取ma的ρ=7.8*10-9kg/mm3，相应理论值与仿真值如表1所示。

表1 有附加质量的音叉梁谐振频率

ma=0时，即无附加质量，则同式(11)

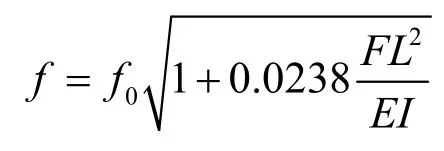
对模型划分网格，如图7所示。

图7 有轴向力的音叉梁有限元仿真

相应理论值与仿真值如表2所示。

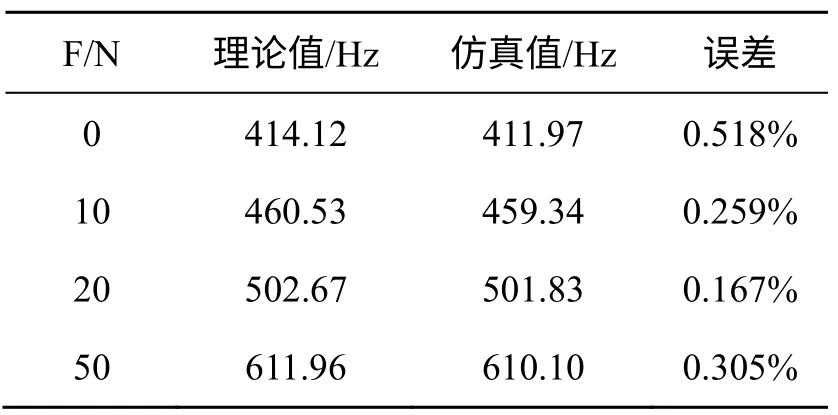
表2 有轴向力的音叉梁谐振频率

F≠0且ma≠0时，即既有轴向力又有附加质量，则同式(15)

取ma的ρ=7.8*10-9kg/mm3，相应理论值与仿真值如表3所示。

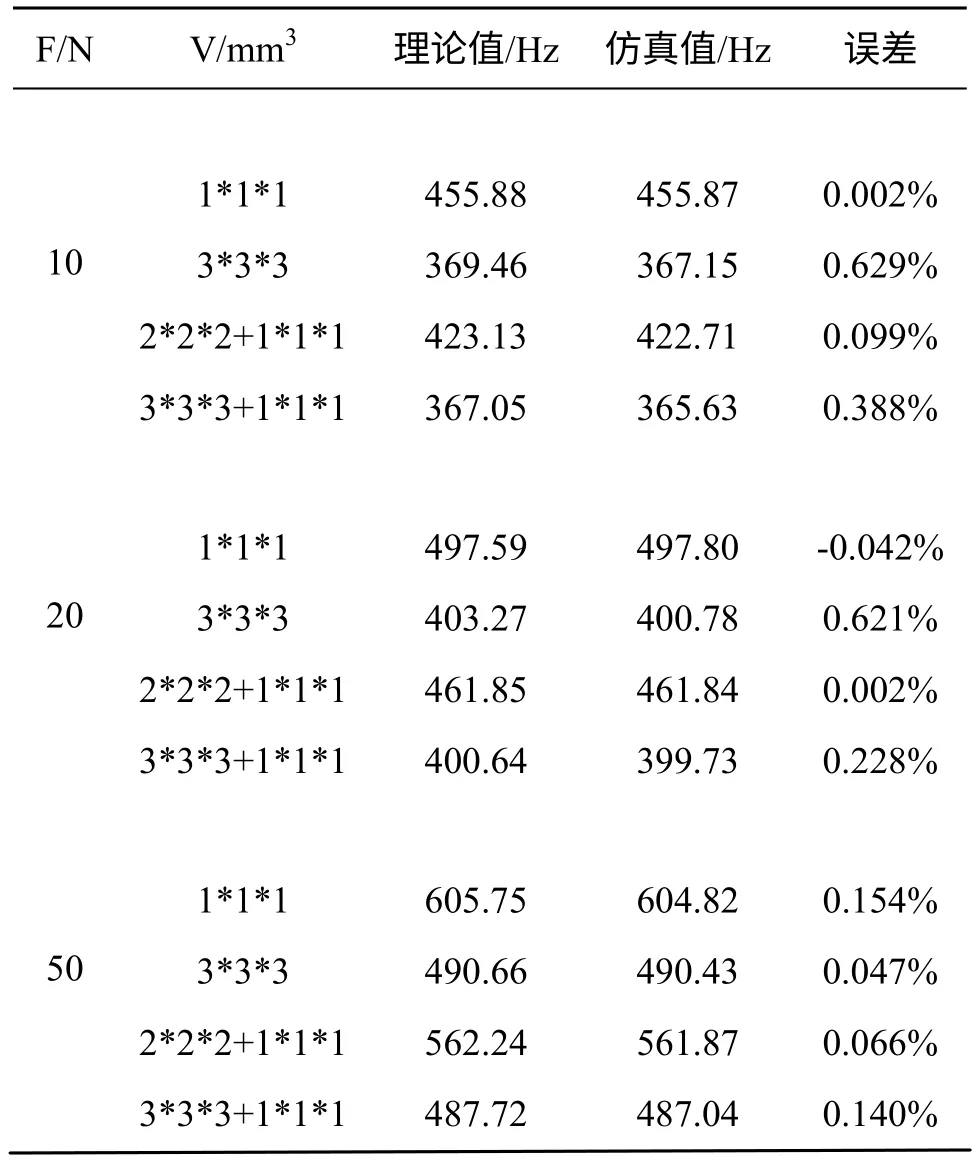
表3 既有轴向力又有附加质量的音叉梁谐振频率

由表1，2，3可以看出：理论计算结果与仿真结果之间的相对误差小于1%，说明了理论模型的正确性。

4 结 论

论文针对携带附加质量的音叉梁，分别建立有轴向力及无轴向力的情况下，具有附加质量的音叉梁在空载及施加附加质量4种情况下的振动模型，并采用有限元方法，对模型的正确性进行验证。结果表明理论与仿真的误差不超过1%，论证了该理论的正确性，进而为谐振音叉附加质量设计提供参考，实现对敏感元件的优化设计。

[1]Cheshmehdoost A, Jones B E, Connor B O.Characteristics of a force transducer incorporating a mechanical DETF resonator [J]. Sensors and Actuarors(A), 1991, 25-27: 307-312.

[2]何高法, 唐一科, 何晓平, 等. 一种新型谐振式微加速度计设计和分析[J]. 微电子技术, 2007, 20(7):273-276.

[3]刘 恒, 张富堂, 何晓平, 等. 静电梳齿微谐振器结构参数化设计[J]. 传感器与微系统, 2009, 28(7):82-85.

[4]刘 恒, 何晓平, 苏 伟, 等. 微机械音叉谐振器动力学分析与仿真[J]. 传感技术学报, 2009, 22(3):325-330.

[5]朱一纶, 王寿荣, 裘安萍. 硅微机械谐振式陀螺仪[J]. 中国惯性技术学报, 2003, 11(4): 45-48.

[6]Hassanpour P A, Esmailzadeh E, Cleghorn V L, et al.Nonlinear vibration of micromachined asymmetric resonators [J]. Journal of Sound and Vibration, 2010,329: 2547-2564.

[7]Hassanpour P A, Cleghorna W L, Esmailzadehb E.Vibration analysis of micro-machined beam-type resonators [J]. Journal of Sound and Vibration, 2007,308: 287-301.

[8]Lee J E Y, Bahreyni B, Seshia A A. An axial strain modulated double-ended tuning fork electrometer [J].Sensors and Actuators (A), 2008, 148: 395- 400.

[9]Cabuz C, Cabuz E I, Ohnstein T R. Factors enhancing the reliability of touch-mode electrostatic actuators [J].Sensors and Actuators, 2000, 79: 245-250.