射影线束形成的二阶曲线及其退化形式

2012-03-21刘阜平

图学学报 2012年4期

刘阜平，丁勇

（太原理工大学机械工程学院，山西太原 030024）

共底射影对应平面αα'，成透射位置时，其所有对应线束形成的二阶曲线全部出现退化。但是，如果不成透射位置时，他们的对应线束形成的二阶曲线为圆、椭圆、双曲线和抛物线，这些二阶曲线共同组成的图谱丰富多彩。当我们固定一个场α不动，让另一个场α'平移、旋转运动时，二阶曲线类型不仅按照一定规律变化，而且退化形式也有多种。

1 二射影对应平面场特殊线束形成的二阶曲线

任给二射影对应平面场α(A，B，C，D…)α′(A′，B′，C′，D′…)，我们可以容易的作出两对对应合同线束SS′、HH′，其中SS′为同向，HH′为异向；两对对应合同点列ll′、kk′，u′v直线分别对应两场的非固有直线[1]。如图1 所示且存在3种对应线束。

图1 二射影对应平面场αα′

图2 一对非对非线束形成双曲线

第1种，底为非固有点对应非固有点的唯一一对对应线束p∞p∞′，简称非对非。它们形成的二阶曲线为双曲线，渐近线为u′v，如图2所示。如果我们平移其中一个射影平面场并不改变p∞p∞′形成双曲线的类型和渐近线的方向。

第2种，底为固有点对应非固有点的线束，即u′v线上的点与其非固有对应点的二线束，简称固对非。他们形成的二阶曲线为抛物线，如图3所示。抛物线的轴线是非固有点方向，这种抛物线只有在二平面场成透射时才出现退化。

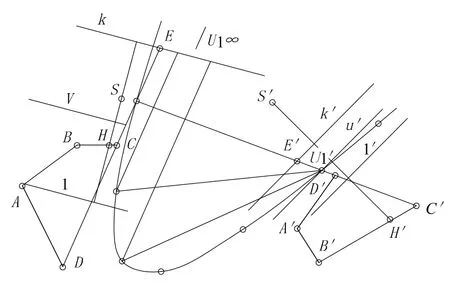
图3 固对非线束形成抛物线

第3种，底为固有点对应固有点的线束，简称固对固。其中特殊的两对合同线束，SS′同向形成二阶曲线为圆，HH′异向形成二阶曲线为双曲线，如图4(a)所示。HH′形成双曲线的渐近线可以通过反射线束H′成H0′得到，如图4(b)所示。他们的渐进线是一对垂直的直线，因此HH′形成的双曲线是等边双曲线。有趣的是，当αα′二场中的合同点列相交于一对对应点时，HH′形成的双曲线退化成两条相互垂直的直线，如图5所示。

图4 同向合同线束形成圆异向合同线束形成等边双曲线

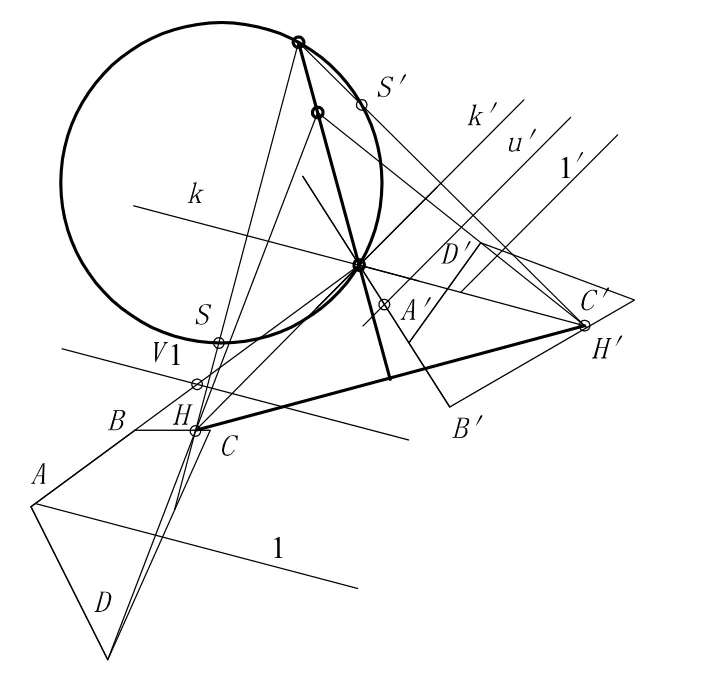
图5 合同点列相交时异向合同线束HH′退化成直线

2 一般固对固线束形成的二阶曲线

一般固对固线束，若平移其中一对对应线束，不改变他们形成二阶曲线的类型。因此，我们可以通过二线束平移共底后二重直线的数量来判断其二阶曲线类型。

异向对应线束形成双曲线。

同向对应线束有3种情况：椭圆，双曲线和抛物线。为了说明这个问题，我们引进任意二射影对应线束的度量问题[2]。二射影对应线束的“大小”，可以由他们的一对对应主直线mm′、nn′和一对对应“等角线”xx′、yy′来确定。xx′、yy′是二线束平移旋转后，异向共底对合的二对对应二重直线。

任取二射影平面场中EE′对应点为底的同向线束，形成二阶曲线为椭圆，这说明如果EE′共底一定无二重直线，如图6所示。如果我们固定E线束不动，让E′旋转到xx′平行位置，这时形成的二阶曲线为抛物线，见图7。yy′平行时为另一种抛物线位置，而且仅有这两种位置为抛物线，其余为双曲线和椭圆（图略）。

图6 固对固同向线束形成椭圆

图7 固对固同向线束形成抛物线

3 二阶曲线的退化

关于二阶曲线的退化，用解析几何来讨论，认为有3种形式[3]。其中第2种“相交于一个实点的两条虚直线”可能欠妥，因为虚直线上无实点。在这里借助于图表的方式可以细分为11种，如表1所示。

从表1中可以看出，二次曲线退化形式并不与其类型相匹配，即不能称为抛物型退化，椭圆型退化或双曲线型退化。如非对非线束形成双曲线，其中Aa型退化与固对固线束中抛物线Aa型退化相同。这种分类方式体现了射影对应中不同元素之中有相同，相同元素之中有不同的变化形式和规律。

4 关于二阶曲线的一点说明

如果我们抛开共底二射影对应平面场αα′，单独讨论二射影对应线束，那么非对非线束形成的双曲线与固对固线束形成的双曲线是可以互相转换的，见图2。但是他们的退化形式却是有区别的，固对固平移共底后成Ab型退化；而非对非平移后不退化，旋转共底后出现Aa、Ba、Oa型3种退化，如表1所示。当然，固对非线束和固对固线束形成抛物线也一样。所以，是孤立地讨论二射影线束还是放在二射影平面场αα′中，或者放在二仿射平面场中是不一样的。如二射影场中固对固线束和二仿射场中固对固线束虽然一样，但非对非线束就不一样，因为前者是射影的，后者却是仿射的（参照相似点列与射影点列的区别）。

5 结束语

二射影对应平面交“线”是什么？通过上述讨论，可以知道，这个“线”是变化不定的。因为射影平面中点和点是不同的（属于点的线束不同），这些不同线束中的对应直线交点形成的“线”有圆、椭圆、抛物线和双曲线，当然也可以是直线和点。这些“线”随着二平面位置不同而变化。在欧氏平面中被看成不同几何元素的点、直线、圆、椭圆、双曲线和抛物线，在非欧平面上都可以用一种几何元素即射影线束来生成。这些对我们进一步研究射影空间是很有帮助的。