用四元数描述飞行器姿态时的几个基本问题

范奎武

海军驻航天一院军代表室，北京100076

爱尔兰数学力学家哈密尔顿于1843年发明四元数，之后四元数用于描述刚体在三维空间中的姿态。描述刚体姿态的还有姿态角(欧拉—克雷洛夫角)和方向余弦矩阵。在建立飞行器运动的数学模型时，可以初步把它们看作是刚体。现在四元数在飞行器捷联式惯性导航系统中得到了广泛使用。建立四元数与方向余弦矩阵之间的关系，描述刚体合成转动的四元数与欧拉角之间的关系，推导出四元数微分方程，这是初学四元数时会遇到的3个难理解的问题。以下将叙述并推导这些问题。

1 四元数的定义与表示方法的简要回顾

四元数由1个实数单位和3个虚数单位组成

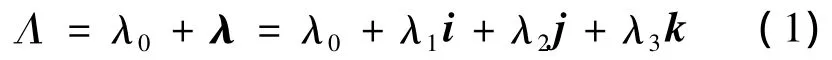
式中i，j，k是正交单位矢量，与平面内的复数相似，可以用向量式、复数式、指数式、三角式及矩阵式等多种形式表示四元数。

定义四元数的范数为

于是，有

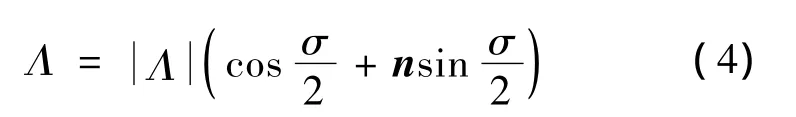
在定义了四元数之后，相应地定义了相等与数乘、四元数之间的乘法。四元数乘法服从结合律，但不服从交换律，四元数的乘法和加法服从乘法对加法的分配律。文中用“◦”表示四元数相乘。

与Λ标量部分相同，向量部分反号的四元数λ0－λ称为Λ的共轭四元数，记为Λ*=λ0－λ。

2个四元数的乘积的共轭四元数等于这2个四元数各自的共轭四元数以相反的顺序相乘的乘积，即

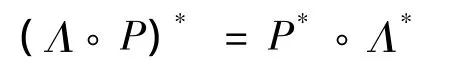
上式可以推广到2个以上四元数乘积的情况。

即

对规范化四元数，有Λ－1=Λ*。当Λ≠0，P≠0时，有

同理可以推广到n个四元数乘积的共轭四元数情况

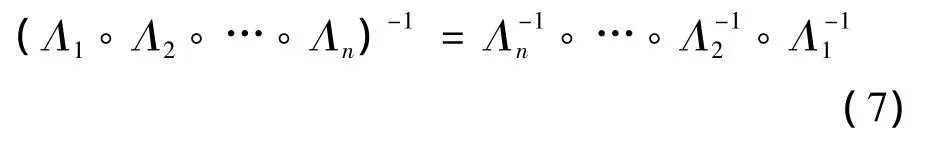
2 用四元数描述刚体的定点转动

设起始时刻惯性坐标系OIxIyIzI与体轴坐标系OIxbybzb重合，A为刚体上的一点，位置向量r=OA，刚体绕过原点O的瞬时轴n转过角度σ时，r变成新位置r1=OB，体轴坐标系 OIxbybzb也转到新位置，如图1所示。

图1

设在坐标系OIxIyIzI中，向量r和r1的分量列阵分别是［x，y，z］T和［x1，y1，z1］T，r0是任意常数，定义由矢量r和r1生成的2个四元数

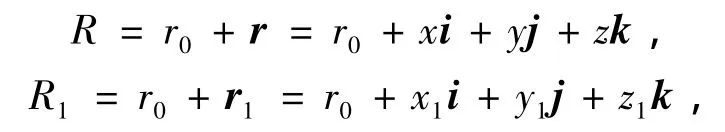
若令

结合图1，可以证明有下面的关系式成立［1-2］

形如Λ◦()◦Λ*的算子称为转动算子，它确定了绕瞬时轴n转角为σ的转动。因为

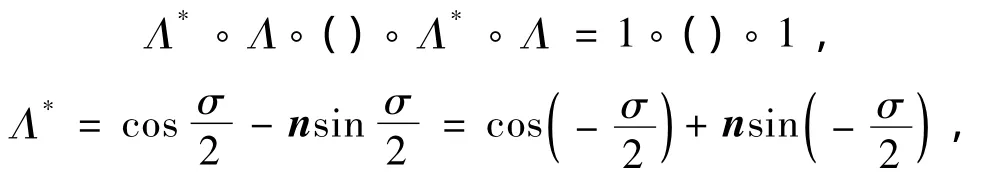
所以转动变换Λ*◦()◦Λ给出了绕－n轴转过角度σ的转动。

3 四元数与方向余弦矩阵的关系

按照四元数相乘的矩阵形式［1］，可以把(9)式写成

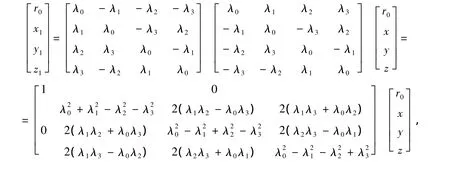
这是一个矢量转动前后，其在同一个坐标系的投影与描述转动的四元数之间的关系。实际上需要的是坐标系转动前后同一个矢量在不同坐标系的分量与描述转动的四元数之间的关系，即方向余弦矩阵。

把坐标系OIxIyIzI和OIxbybzb中坐标轴上的单位矢量记为iI，jI，kI和ib，jb，kb，把它们对应地看作是转动前后的矢量 r和 r1，设 ib，jb，kb在坐标系OxIyIzI中 的 投 影 分 别 为 ［ibxIibyIibzI］T，［jbxIjbyIjbzI］T，［kbxIkbyIkbzI］T则根据(9)和(10)式，有

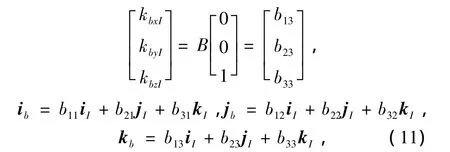
设向量r在这2个坐标系内的投影分别是［xIyIzI］T，［xbybzb］T，则有

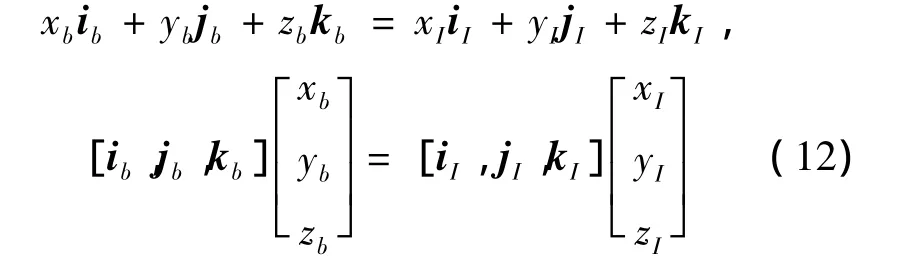
根据(11)式，把(12)式的左端化为

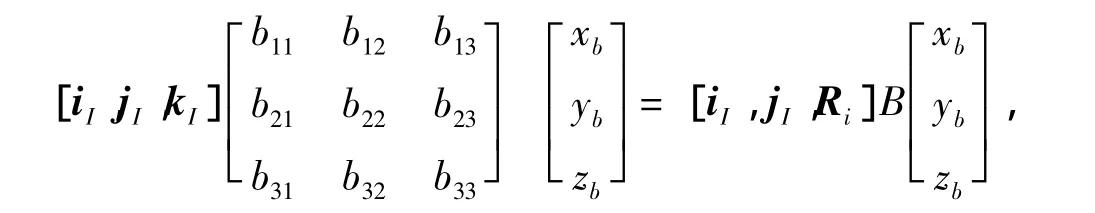
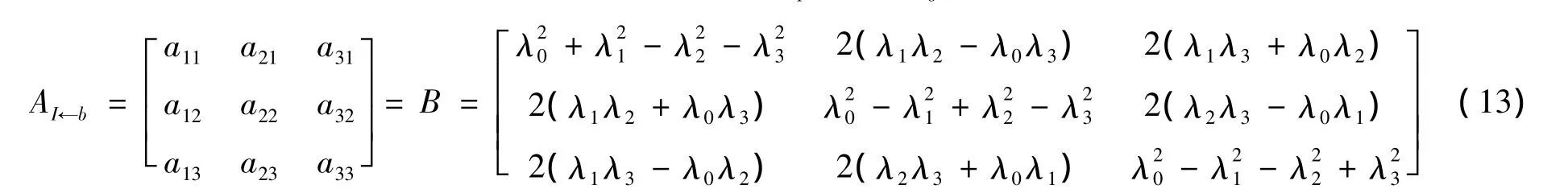
即从坐标系Oxbybzb到OxIyIzI的坐标变换矩阵是(13)式，这是解析表达的方法。

用向量r在OxIyIzI和Oxbybzb这2个坐标系内的投影［xIyIzI］T，［xbybzb］T生成四元数RI和Rb，即

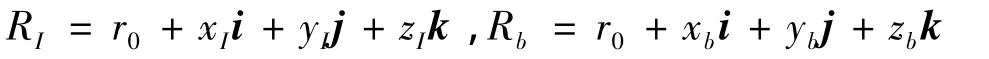
则可得出

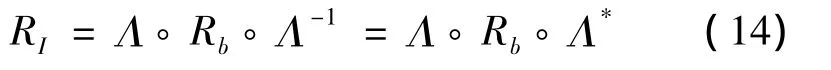
4 多次转动的合成四元数

如果刚体依次进行2次转动，它们分别由四元数Λ1和Λ2表示(瞬时轴通过同一点)，则有

这说明刚体依次进行由Λ1和Λ2表示的转动，等效于由四元数Λ2◦Λ1确定的一次转动。对于多次转动的情况，有

以垂直发射的飞行器为例，设由发射惯性系OxIyIzI绕OzI轴转动俯仰角 φ得到Ox1y1z1，再绕Oy1轴转动偏航角ψ得到Ox2y2z2，再绕Ox2轴转滚动角γ得到体轴系Oxbybzb，如图2所示，则从发射惯性系到体轴系的坐标转换矩阵为:

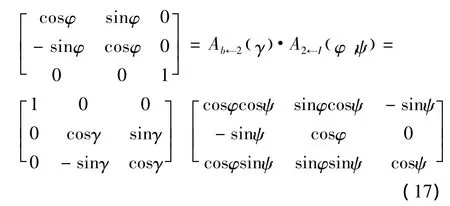
于是可以写出合成转动的四元数

其中n1，n2，n3分别是OzI，Oy1，Ox2轴上的单位矢量，这3个轴在发射惯性系OxIyIzI内的方向余弦分别是［0，0，1］，［－sinφ，cosφ，0］，［cosφcosψ，sinφcosψ，－sinψ］，根据描述转动的四元数的定义，得出合成转动的四元数是:

可见，用这种顺序相乘时，过程非常繁琐。还有一种简便的方法，以三次转动为例，由(16)式得出

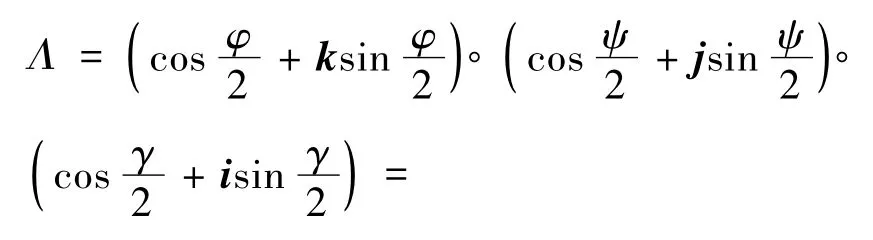
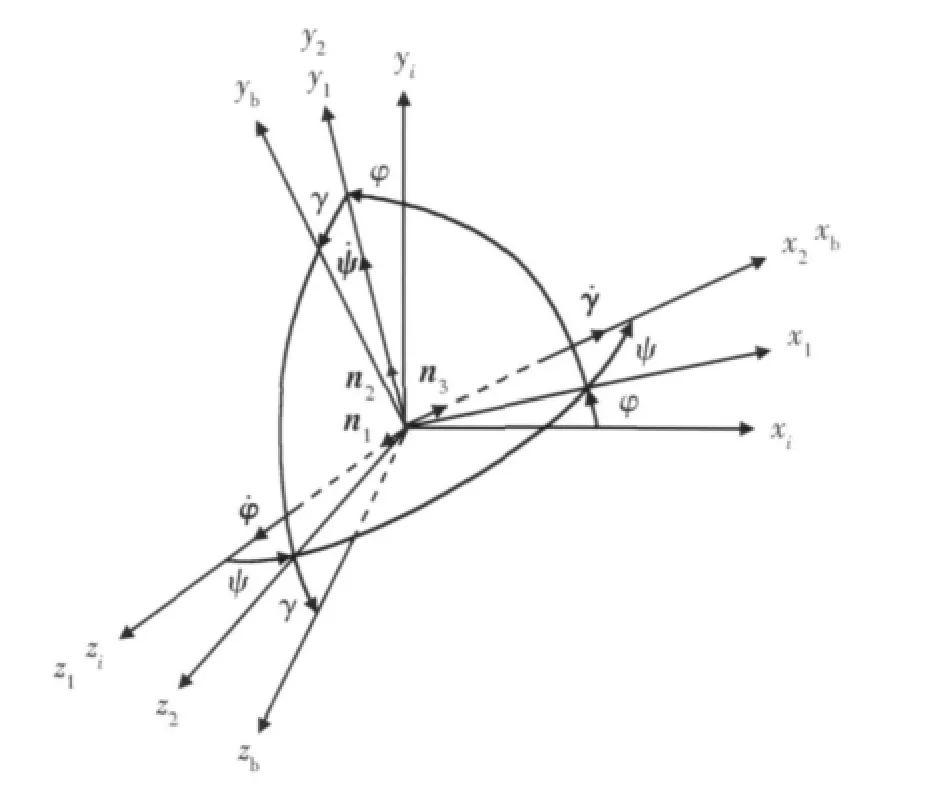
图2 3次转动的示意图

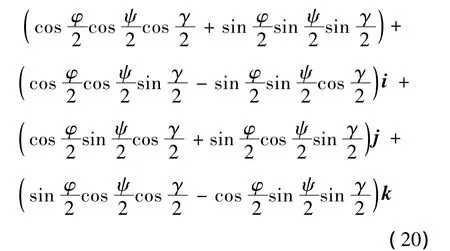
可以验证与(19)式的结果相同，但却明显化简了推导过程。因此，可以把绕相应的坐标轴进行转动的合成四元数的确定方法简单记为:1)在每次的新坐标系里列写四元数，但虚部的单位还是最初的坐标系内的单位;2)相乘的顺序是对应于转动的先后顺序从左到右相乘，与合成转动的方向余弦矩阵相乘顺序正好相反。

对于多次转动的合成四元数求取情况［3］，第2种相乘顺序能明显简化推导过程。文献［4］中给出的有限转动的交换定理可以说明这两种相乘顺序的理论依据。

5 四元数微分方程

方向余弦矩阵形式的转动微分方程是

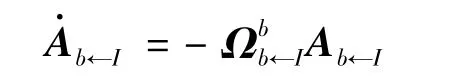
写成矩阵形式为

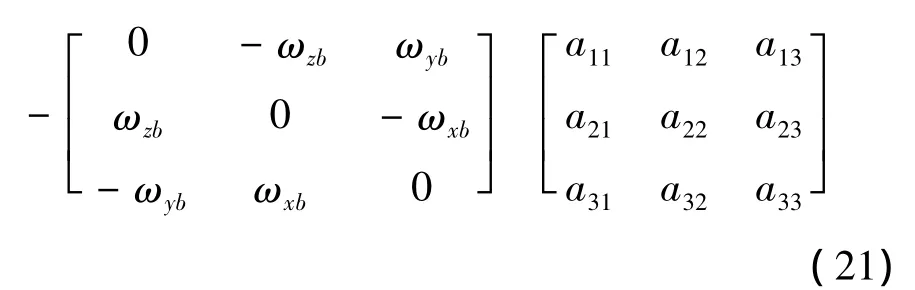
式中

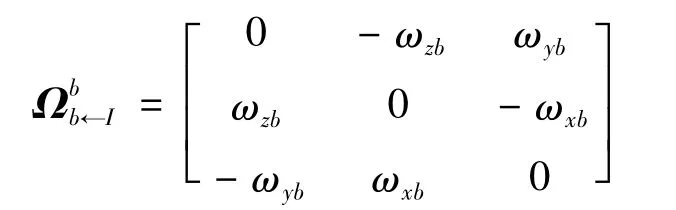
是用坐标系Oxbybzb相对OxIyIzI的转动角速度在坐标系Oxbybzb中的投影［ωxb，ωyb，ωzb］T生成的反对称矩阵，刚体的姿态在随时间变化，所以描述姿态的四元数也是时间的函数，因此，存在四元数微分方程。

文献［1-2］给出了根据四元数的运算性质推导其微分方程的方法。下面介绍利用方向余弦矩阵形式的转动微分方程及四元数与方向余弦矩阵之间的关系推导四元数微分方程的方法［5］。由(13)式，得出

于是，再利用(21)式，就可以得出

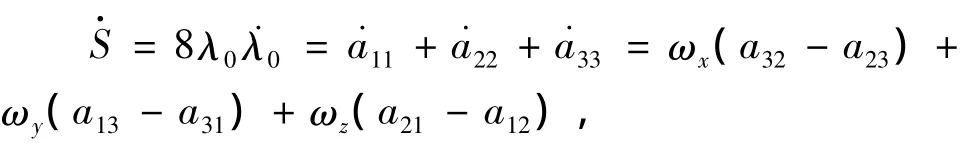
把上式中方向余弦矩阵的元素用四元数表示，整理得

由此得出对λ0的微分方程

把方程组(22)式中的第2，3，4式分别对时间求导数，类似前面推导过程得出

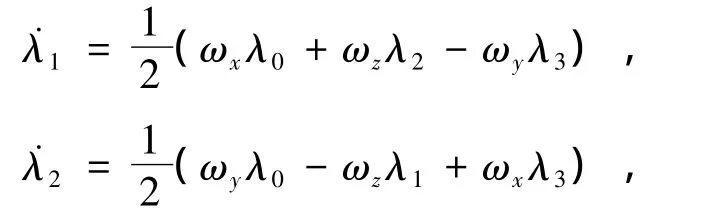
写成矩阵形式为

在捷联惯导系统中，运动体角速度直接由速率陀螺测得，若把采样时刻内运动体转动的角速度视为常量，则描述转动运动的方向余弦矩阵微分方程和四元数微分方程都有解析解，作者用拉普拉斯变换法的方法求出了具体表达式，见文献［3］。

6 小结

本文给出了方向余弦矩阵与四元数之间关系的推导方法，证明了合成转动四元数的求取方法，介绍了四元数微分方程的推导方法。四元数在描述刚体姿态、多体系统动力学、计算机图形、人造地球卫星轨道、弹性力学、电动力学、电磁学、偏微分方程等领域都得到了应用。当前四元数理论与方法仍在发展，已经扩展到八元数并在相关领域得到应用。

［1］ 以光衢.陀螺理论与应用［M］.北京航空航天大学出版社，1990，11.

［2］ 秦永元.惯性导航［M］.科学出版社，2006，5.

［3］ 范奎武，刘竹生.水下弹射模型弹弹道复现算法［J］.导弹与航天运载技术，2007，(1):1-5.

［4］ 贾书惠.刚体动力学［M］.北京:高等教育出版社，1987.

［5］ И.Ф.Кавинов.Инерциальная навигация в околоземном пространстве［M］.машиностроение，1988.

［6］ 勃拉涅次，等.梁振和，译.四元数在刚体定位问题中的应用［M］.国防工业出版社，1977，8.

［7］ 耿长福.航天器动力学［M］.中国科学技术出版社，2006，9.