复式河槽平均局部阻力系数的研究

赵红旭，关雅迪

(1.国电电力发展股份有限公司，黑龙江牡丹江157000;2.大连大学，辽宁大连116622)

0 引言

SKM方法是以平均水深的N—S方程为基础提出的，因其可较准确反应漫滩水流的现象而被广泛应用，其解析解计算式中有3个重要的参数分别为涡黏系数λ、二次流项Γ及达西阻力系数f。其中达西阻力系数f不同于传统达西公式，通过其定义(f=8τb/ρUd2)及许多学者［1，7－10］的研究发现将SKM法的达西阻力系数称为平均局部阻力系数更为合适。达西阻力公式在知道复式河槽各区断面平均流速时可准确推算各区流量及总流量，但在实际测量中由于滩槽掺混作用很难准确测得各区断面平均流速，因此要准确得到各区达西阻力系数就变得很困难。所以在实际测量中可用SERCFCF系列试验的方法，用LDV测垂向点流速Ui，用普雷斯通管测量对应垂线的床面剪切力τbi，后用上述定义式求得局部阻力系数再平均求得复式河槽各区平均局部阻力系数，修正后可准确推求总过流量。

许多学者(Shiono［1］，Knight［2－3］，Rameshwaran［4］，Rezaei［5］，Ervine［6］，Liao［7－8］，Tang［9－10］，槐 文 信［11－12］，杨 中华［13－14］及许唯林［15］等)在研究SKM法时均采用这一平均局部阻力系数。Shiono和Knight［1］在提出SKM方法时即给出了平均局部阻力系数计算式并拟合了主槽与滩地阻力系数与相对水深的关系式。Liao［7－8］研究了平均局部阻力系数对于SKM法解析解的影响。Rameshwaran［4］发现主槽和滩地的平均局部阻力系数与相对水深存在一定关系。综上可得，在研究SKM法时必然会涉及到平均局部阻力系数的计算，因此，探索其规律就显得尤为重要。

本文重点研究复式河槽各区的平均局部阻力系数，探讨各区平均局部阻力系数的相互关系，进而通过反算推求断面总过流能力，并推求平均局部阻力系数与达西公式的转换关系。

1 局部阻力系数分析与计算

本文运用SERC—FCF的水槽试验资料(详见表1)，给出了每个系列各区局部阻力系数平均值与相对水深(Dr=(H－h)/H)的关系(如图3～图5)。各区平均局部阻力系数值采用下式计算为:

式中:fij、τbij和Udij分别为第i区j点的局部阻力系数、局部剪切力和局部平均流速;ρ为水体密度。

复式河槽断面形态如图1所示，其中可划分为4个区域:主槽区(4区)、掺混区(3区)、滩地区(2区)和滩地边坡区(1区)。这里给出(1)式计算得到的FCF0804组资料主槽和滩地局部阻力系数见图2。

各系列滩地平均局部阻力系数f2随相对水深Dr的关系如图3，随着Dr增大，f2减小。试验资料表明f2与相对水深为0.25的f2(0.25)之比与Dr满足乘幂关系，如图4。关系式如下

主槽与滩地平均局部阻力系数之比f4/f2与Dr满足抛物线分布，如图5所示。可以看出它们的比值满足二次函数，其关系式如下

在边壁区平均局部阻力系数f1受到边壁影响，但图6表明，f1与f2可认为相等。图7说明主槽边坡平均局部阻力系数f3与(f2+f4)/2有一定线性关系，可用下式计算

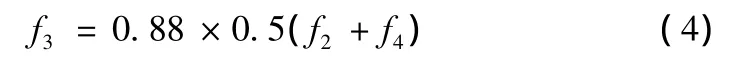
表1 复式河槽系列试验断面形态资料

2 流量估算

在推求复式河槽过流能力时，用各区达西阻力系数推求整个过留断面流量的方法已被证明具有较高精度［16］。其计算公式为:

本文用平均局部阻力系数来反算复式河槽过流能力。各区流量可表示为:

式中:Qi为第i区过流量;Ai为第i区过流断面面积;fi为第i区平均局部阻力系数;其余参数同上。

总过流量为

根据前述的各区阻力系数关系求得SREC－FCF03的资料在不同相对水深下的总过流量。实测流量和计算流量如图8所示。可以看出计算值较实测值大，说明平均局部阻力系数较(5)式计算的阻力系数有一定偏差，需对其值进行修正。

图1 复式河槽断面形态图

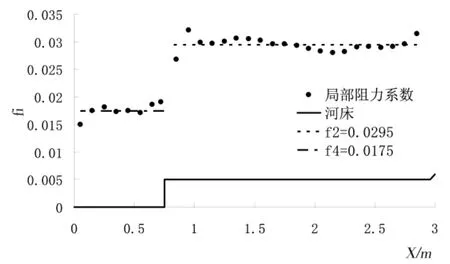
图2 主槽和滩地平均局部阻力系数f4和f2(FCF0804)

图3 滩地平均局部阻力系数随相对水深的变化

图4 滩地平均阻力系数f2和f2(0.25)之比与相对水深的变化关系图

图5 主槽和滩地平均阻力系数随相对水深的变化图

图6 滩地边坡区与滩地区局部阻力系数的关系图

图7 主槽边坡区与主槽和滩地区平均阻力系数的关系图

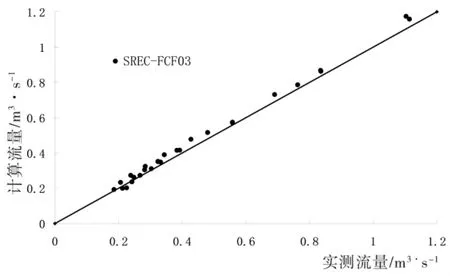
图8 计算流量与实测流量比较图

图9 主槽区阻力系数与平均局部阻力系数随相对水深的变化

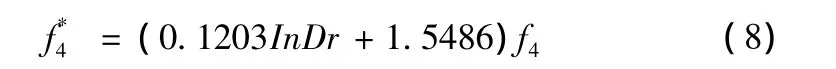
图10说明滩地阻力系数f2与平均阻力系数表现出一定线性关系，经拟合得

将(1)式计算出的平均局部阻力系数用(8)(9)式进行修正，再用修正后的平均局部阻力系数反算过流量，如图11所示，从图中看出修正后的平均阻力系数估算断面过流量比较准确，平均相对误差为1.4%。

3 结论

1)本文研究基于SERC—FCF的系列试验资料，结论可运用于水槽试验中，在天然河道中的平均局部阻力系数需用实测资料进一步率定。

2)滩地平均局部阻力系数随相对水深的增加而减少，将其无量纲后于相对水深符合成乘幂关系，主槽和滩地平均阻力系数之比与相对水深满足二次函数;滩地边坡和滩地平均阻力系数相等;主槽边坡平均阻力系数可用主槽和滩地平均阻力系数函数表示。

3)滩地平均阻力系数与达西阻力系数满足线性关系，而主槽两值之比呈对数分布。

4)用平均局部阻力系数推算的断面总过流量较实测值偏大，经过修正后，其值推求的计算流量与实测值吻合较好，平均相对误差为1.4%。

图10 滩地区阻力系数与平均局部阻力系数的关系图

图11 修正后的计算流量和实测流量比较图

［1］K Shiono，D Knight.Turbulent open－channel flows with variable depth across the channel［J］.Journal of Fluent Mechanism，1991，222(5):617－646.

［2］D Knight，M Omran and Xiaonan Tang.Modeling depth－averaged velocity and boundary shear in trapezoidal channels with secondary flows［J］. Journal of hydraulic engineering ASCE，2007，133(1):39－47.

［3］D Knight，B Abril.Refined calibration of a depth－averaged model for turbulent flow in a compound channel［C］.Process Institution of Civil Engineers，Water，Maritime and Energy，London，paper 11017，118，151－159.

［4］P Rameshwaran，K Shiono.Quasi two－dimensional model for straight overbank flows through emergent vegetation on floodplain［J］.Journal of Hydraulic Research，2007，45(3):302－315.

［5］B Rezaei，D Knight.Application of the Shiono and Knight Method in compound channels with non－prismatic floodplain［J］.Journal of Hydraulic Research，2010，47(6):716－726.

［6］A Ervine，K Babaeyan－Koopaei and R Sellin.Two－dimentional solution for straight and meandering overbank flows［J］.Journal of hydraulic engineering ASCE，2000，126(9):653－669.

［7］Huasheng Liao，D Knight.Analytic Stage－discharge formulas for flow in straight prismatic channels［J］.Journal of hydraulic engineering ASCE，2007，133(10):1111－1122.

［8］Huasheng Liao，D Knight.Analytic Stage－discharge formulas for flow in straight trapezoidal open channels［J］.Advances in water resources，2007，(3):2283－2295.

［9］Xiaonan Tang，D Knight.Analytical models for velocity distribution in open channel flows［J］.Journal of Hydraulic Research，2009，47 (4):418－428.

［10］Xiaonan Tang，D Knight.Lateral depth－averaged velocity distributions and bed shear in rectangular compound channels［J］.Journal of hydraulic engineering ASCE，2008，134(9):1337－1342.

［11］槐文信，耿川，曾玉红，等.部分植被化复式河槽紊流时均流速分布解析解［J］.应用数学和力学，2011，32(4):437－445.

［12］槐文信，徐治刚，杨中华等.部分植被花复式河道水流的二维解析解［J］.应用数学和力学，2008，29(8):976－983.

［13］杨中华，高伟.考虑滩槽相互作用的漫滩水流二维解析解［J］.四川大学学报:工程版，2009，41(5):42－47.

［14］杨中华，高伟，槐文信.漫滩水流二次流项系数研究［J］.应用数学和力学，2010，31(6):681－690.

［15］许唯林.复式河道漫滩水流计算方法研究［J］.水利学报，2002 (6):21－28.

［16］杨克君，曹叔尤，刘兴年.复式河槽阻力系数及过流能力计算［J］.水科学进展，2005，16(1):23－27.