拓扑灰预测模型在河川径流量预测中的应用
2012-03-20戴然
戴然
(安徽省水利部淮河水利委员会水利科学研究院,安徽蚌埠233000)
0 引言
河川径流量的预测,已成为当今水资源开发和利用中不可缺少的非工程措施之一。对于科学治水、防洪调度、减少灾害等方面,都起到不可替代的作用。一次准确的预测信息能够收到可观的经济效益和社会效益。建国后在长江、黄河、海河、松花江等江河流域多次大洪水的抗洪斗争中,都已显露出径流预报的巨大威力。特别是在抗御1998年长江、嫩江、松花江特大洪水中,充分发挥了径流预测的科学性、主动性作用,为减少经济损失做出了巨大贡献[1-2]。
1 拓扑灰预测模型
1.1 拓扑灰预测模型简介
20世纪70年代末期,我国著名学者邓聚龙提出了灰色系统理论,认为一切随机量都是在一定范围内、一定时段上变化的灰色量和灰过程。对于灰色量的处理不是寻求它的统计规律和概率分布,而是将杂乱无章的原始数据列,通过一定的方法处理,变成比较有规律的时间序列数据(以“数找数”的规律),再建立动态模型,即灰色模型[3]。
灰色拓扑模型对于地表径流量序列,一般都是大幅度摆动序列,对这一种序列,最有效的方式是用灰色拓扑模型进行预测:按点集拓扑基选取时分布序列,进行建模,预测拓扑基的时分布,以达到预测摆动序列未来发展态势的目的。它用模型预测未来发展变化的整个波形。因为许多点可以构成一个波形,所以拓扑预测是规定许多的给定值,对每一个给定值,都可在给出的曲线上得到一组点分布数据,然后对每一个分布分别建立灰色模型,预测这组给定值未来发展变化的时间间隔[4]。
1.2 拓扑灰预测建模方法
假设某一数据列x(0)在二维平面上,按点(k,x(0)(k))可以描绘出曲线x(0)。为了预测整个曲线的未来发展变化,可以根据曲线x(0)的变化范围(最大值与最小值之间)和变化幅度(最大值与最小值之比),人为地给定一系列阈值ξ,i =1,2,…,m,记x(0)中最大数据为max x(0),最小数据为min x(0),即
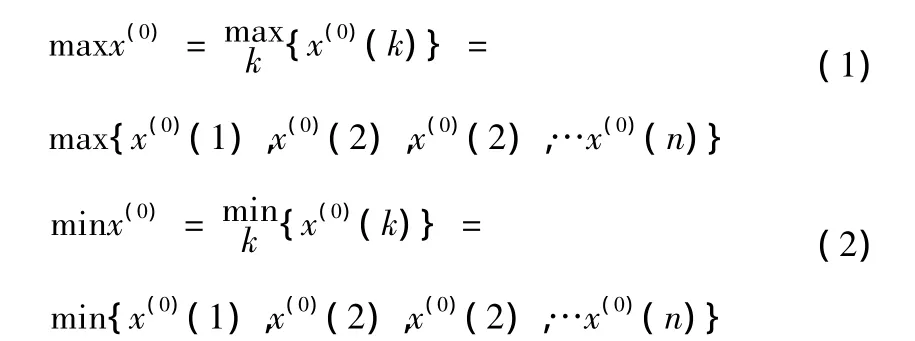
则有

对每一个阈值,有下述映射

mti(0)(k)是水平线ξ与曲线x(0)相交的第k点横坐标值,并有下述映射:

P为横坐标投影算子

并有映射为:

对ω作ni次AGO生成(累加生成),有

对ωi
(1)建立GM(1,1)模型(灰色单个变量模型),有
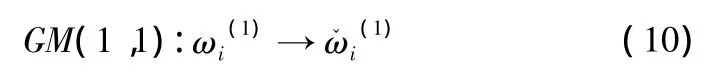

为此,有全过程为

将所有的点(li,ξi),∀i∈{1,2,…m}联成曲线,有,

即为拓扑灰预测曲线[6~10]。
2 应用实例
2.1 沂河概况
沂河又名沂水,在山东省南部、江苏省北部,为淮河一级支流,源出山东省沂源县田庄水库上源东支牛角山北麓,北流过沂源县城后折向南,至江苏省邳县吴楼村入新沂河,抵燕尾港入黄海。全长574 km,流域面积17 325 km2,主要支流有东汶河、蒙河、柳青河、孝河、涑河等。大小支流百余条,集水面积4 892 km2,河床最宽为1 540 m。属山洪河道,源短流急,洪水集中。
流域内沂源、沂水、沂南、临沂、蒙阴、平邑、费县、郯城等县全部或大部皆属沂河流域,在郯城县吴道口村南出境入江苏省。流域最上游以鲁山背斜与潍、弥河分水,东以沂山背斜余脉与沭河分水,地形西北高,向东南部倾斜,自河源至东汶河口,大部为山区,山峦迭嶂,海拔高程300~800 m,斜午、青驼、茶山西北多为低山丘陵及高地,地面高程在200~400 m,蒙山前半程以南地势变缓向平原过渡,在临沂城北与其支流祊河汇流后进入中游临郯苍平原。平原坡缓 1/3000~1/2000。沂河水文站1981—2000年年径流量见表1。

表1 沂河水文站1981—2000年年径流量一览表
2.2 沂河年径流量的拓扑灰预测
采用沂河水文站1981—1996年共16 a的年径流量(表1)作为特征值,建立年径流量的拓扑灰预测模型,并根据此模型对沂河年径流量进行预测,从而揭示沂河径流量的变化规律。
首先,取定原始非负时间序列X(0)(1)=52877,X(0)(2) =77138,…,X(0)(16)=89580,其中X为年径流量,k=1时表示以1981年的年径流量为时间序列的第一个数值,k=2~n时依次类推。
其次,将数据按点[k,X(0)(k)]绘出折线图,见图1。
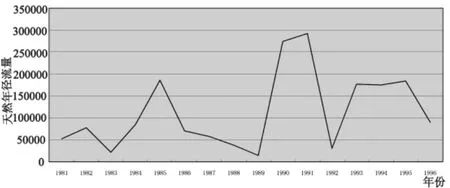
图1 沂河年径流量折线图
再次,取定若干阈值ξi(i=1,2,…,m),并计算每个阈值与折线图的交点的横坐标,得出若干个数列
最后,根据上一步所得的数列建立拓扑灰预测模型群,见表2。如果用不同的阈值进行模型预测得到相同的年份,则取最大阈值作为该年预测的年径流量。

表2 年径流量拓扑灰预测模型
根据表3所得拓扑灰预测模型群预测1997—2000年的年径流量和实测值相对误差见表3。

表3 年径流量预测结果
3 结语
径流预测是减少我国洪涝灾害频繁发生,保证正常供水和水资源合理开发利用的重要手段。随着我国洪涝灾害的频繁发生和国民经济的快速发展,流域内各部门对防洪和供水的预见期也越来越重视,预见期越长,管理和调度起来就越得心应手,否则就会对国民经济造成巨大的损失。
预报精度影响着水资源系统调度规则的经济性和安全性的统一,对水资源系统来说,有些调度规则虽然从长远的利益来说是经济的,但是,由于在某些时候受到安全性的制约,无法付诸实施。只有提高径流预报的技术水平,经济性和安全性才有可能在更高水平上达到统一。
径流预测对我国国民经济可持续健康发展具有重要的意义。随着国民经济的发展,对水的要求则显得日见突出,准确的预估未来很长一段时间内的径流量,可以根据国民经济发展对水的需要,合理的制订蓄放水量,提高水资源的利用效率。
[1]陈亚军,史长莹,郭靖.基于灰色理论的城市用水量预测[J].黑龙江水利科技,2008,36(2):6-7.
[2]严秉忠.二滩水电站中长期入库径流智能预测系统[D].成都:四川大学,2006.
[3]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用:第三版[M].北京:科学出版社,2004.
[4]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.
[5]左书华,李九发,万新宁,等.长江河口年平均流量的灰色拓扑预测与趋势分析[J].水力发电,2005,31(12):19-21.
[6]蓝永超,康尔泗,杨文华.黄河上游径流预报的灰色拓扑方法[J].冰川冻土,1997,19(4):308-311.
[7]张举,丁宏伟.灰色拓扑预测方法在黑河出山径流量预报中的应用[J].干旱区地理,2005,28(6):751-755.
[8]侬学锋,滕孔先,陈植华.基于周期灰色预测的径流量研究及应用[J].广东水利水电,2007(5):40-43.
[9]任政,郑旭荣,刘坤,等.新疆玛纳斯河年径流预报研究[J].水土保持研究,2005,12(5):190-192.
[10]胡斌武.年径流动态的长期灰色拓扑预测[J].水电能源科学,1993,11(1):64-71.
