一个拓展的基于相似性的剩余寿命预测框架

尤明懿

（1.上海交通大学机械系统与振动国家重点实验室，上海 200240；2.中国电子科技集团公司第三十六研究所，浙江 嘉兴 314033）

0 引言

作为故障预测与设备健康管理 （PHM）技术的核心技术之一，基于状态监测的剩余寿命预测技术在近年来吸引了越来越多的研究[1-3]。剩余寿命预测模型的输出构成了设备健康管理的基础[4-7]。目前大多数剩余寿命预测模型试图建立系统衰退过程的全局模型，这对于一些显现出多种衰退模式的复杂系统是比较困难的[4]。基于相似性的寿命预测方法是近来兴起的技术，可以在无需衰退过程建模[8-9]或仅需个体衰退过程建模[10]的情况下给出合理的剩余寿命预测。

基于相似性的剩余寿命预测方法将某服役样本在某一时刻的剩余寿命预测为各个参考样本的局部估计的加权平均。这里，服役样本是指一个正在运行的部件因而在其衰退过程的任何一个状态监测点（即采样点）其实际的剩余寿命是未知的。参考样本是指与服役样本相同的、服役于相同工况下的历史样本。文献 [8]概述了基于相似性的剩余寿命预测方法的假设。

一般地，在衰退过程中建模困难但有大量的历史样本时，基于相似性的剩余寿命预测方法是最有效的。然而，当前相关工作还很少[4,8-14]。大多数（如果不是全部的话）当前基于相似性的剩余寿命预测方法仅利用失效历史样本的衰退过程信息。随着故障预测与健康管理技术的不断发展，将会存在很多失效历史样本有限的场合。另一方面，就有可能存在大量接受预防维护或终止运行的样本。在这种情况下，Tian等[15]报道了通过利用终止运行的历史样本来提升神经网络预测精度的工作。Wang提出[4]的想法也可以用在基于相似性的剩余寿命预测方法中，但并未报道具体的处理方案。此外，存在大量的失效历史样本时，利用接收预防维护或终止运行的历史样本是否有益在文献 [15]中仍未予以研究。进一步地，也有必要探究其它利用接受预防维护或终止运行的历史样本的方法。

本文基于上述考虑，发展一个基于相似性的剩余寿命预测框架以同时利用失效与未失效历史样本。在该框架中，提出两种估计未失效历史样本的寿命，进而利用其衰退过程信息的方案 （记为方案A和方案B）。其中，方案B与文献 [15]中的总体思路相似但技术细节有很大的区别。本文的剩余部分安排如下：第一节给出基于相似性的剩余寿命预测框架，第二节通过一个系统的数值试验评估本文提出的框架，第三节总结全文。

1 建模

1.1 基于相似性的剩余寿命预测方法要素与问题定义

文献 [8]中曾论述了基于相似性的寿命预测方法的思想与要素，这里简要总结这些要素，但在剩余寿命预测方案上有所拓展。基于相似性的剩余寿命预测方法要素如图1所示。

图1 基于相似性的剩余寿命预测方法要素 （其中剩余寿命预测方案有所拓展）

图1中，D代表考察服役样本与参考样本间相似度的时间范围；相似性测度函数S（·）是样本（部件）状态监测变量的函数，用于衡量服役样本与参考样本间的相似度，相似性测度函数可以是欧几里得距离函数[10]、概率函数[10]，或基于模糊逻辑的隶属度函数[9]等。So←→ri（k） 是在服役样本的第k个采样点，服役样本和参考样本间的相似度。权重函数w（·）是相似度的函数，它根据不同参考样本与服役样本的相似度将不同的权重分配给这些参考样本；将相似度代入权重函数就得到了权重w（So←→ri（k））， 为简便计，记为 wi（k）。 最后，在服役样本第k个采样点其剩余寿命预测值PRL0（k）计算为每个参考样本在其各自采样点的 “参考剩余寿命”的加权平均。这里，参考剩余寿命指失效历史样本实际剩余寿命与未失效历史样本估计剩余寿命的集合。需要指出的是，每个参考样本各自采样点 Ni（k） 是在计算相似度 So←→ri（k） 的过程中确定的， 图 1 中以 So←→ri（k） 与 PRLri（Ni（k）） 间的连线表示这一联系。

大多数 （如果不是全部的话）当前基于相似性的剩余寿命预测方法仅利用失效历史样本的衰退过程信息，则剩余寿命的预测方案为：

其中 ARLri（Ni（k）） 为参考样本 i在其第 Ni（k）个采样点的实际剩余寿命，Q为失效历史样本数。

与失效的历史样本不同，未失效的历史样本在其衰退过程中的任何一点ARLri（Ni（k））是未知的，需估计为 ERLri（Ni（k））。 这里， ERLri（Ni（k））指参考样本i在其第Ni（k）个采样点的估计剩余寿命。因此，现在的问题是如何估计ERLri（Ni（k））。该问题可以简化为估计未失效样本失效时间的问题， 因为 ERLri（Ni（k））= （EMi-Ni（k））·△t，其中EMi为未失效参考样本从其第一个采样点至 （潜在）失效采样点数的估计值，△t为状态监测采样间隔。

1.2 利用失效与未失效历史样本的基于相似性的剩余寿命预测框架

本小节首先提出两种估计未失效历史样本寿命估计方案，进而给出利用失效与未失效历史样本的、基于相似性的剩余寿命预测框架。

在第一个方案 （方案A）中，未失效历史样本的EMi首先通过仅利用失效样本的、基于相似性的剩余寿命预测方法予以估计。然后，基于所有失效与未失效历史样本再预测服役样本的剩余寿命。使用方案A的、基于相似性的剩余寿命预测框架如图2所示。

图2中，Q为失效样本数，P为未失效样本数，H为非负整数且 （H+1）·△t=D （参看图1），这意味着连续 （H+1）个采样点用于衡量服役样本与参考样本间的相似度。图2中，估计过程指估计EMp的过程，执行过程指使用全部历史样本预测服役样本剩余寿命的过程。估计过程中，使用未失效样本接受预防维护或终止运行前最后的 （H+1）个点以估计EMp，因为它们反映了样本最接近其 （潜在）失效时刻的状态。

在第二个方案 （方案B）中，与方案A对每个未失效历史样本EMp一一估计的方法不同，对所有未失效样本的EMp同时予以估计。使用方案B的、基于相似性的剩余寿命预测框架如图3所示。

图2 使用方案A的基于相似性的剩余寿命预测框架

图3中，该框架的执行过程与图2中的一致。然而，图3中的估计过程与图2中的有很大的区别。估计过程的总体思想是同时估计EMp以优化基于相似性的剩余寿命预测方法在预测失效历史样本剩余寿命时的总体表现。图3中，同时估计EMp的原因是它们在执行过程中也是同时被使用。值得指出的是，与这里的方法不同，Tian等[15]对接受终止运行的历史样本寿命进行一一估计；同时，在文献[15]中神经网络的输入、输出也与基于相似性的剩余寿命预测方法不同。仅用失效历史样本进行表现评估的原因是，只有它们在其各个采样点的实际剩余寿命是已知的。估计过程中每次仅对一个失效历史样本的剩余寿命进行预测的原因是，这样可以使评估过程中使用的 （Q+P-1）个参考样本最接近执行过程将要使用的 （Q+P）个参考样本。图3中，总体表现是根据需要定义的，可以是均方差[15]，平均预测误差[8]，SCORE指标[16]等。也可以定义这样的一个总体表现指标，给予接近样本失效时的预测误差更高的权重。

图3 使用方案B的基于相似性的剩余寿命预测框架

1.3 示例

本小节给出一个利用失效与未失效历史样本的基于相似性的剩余寿命预测方法示例。

图1中，要素D已在1.2小节予以讨论。实际中，D（或H）的取值可以根据操作经验进行确定。一个主要的法则是最近的连续 （H+1）个采样点应能反映样本的当前状态。

与文献 [8]一样，本文采用距离函数：

式 （2） 中， s （k，H，i，m） 计算了服役样本在时段[（k-H）·△t，k·△t）]中的状态监测变量与参考样本 i在时段 [（m-H）·△t，m·△t）] 中的状态监测变量的距离，其中服役样本k≥H+1，失效参考样本H+1≤m≤Mi，未失效参考样本H+1≤m≤Gi。这里，Mi为失效参考样本从其第一个采样点至失效的采样点数，Gi为未失效参考样本从其第一个采样点至接受预防维护或终止运行前最后一个采样点的采样点数。需要指出的是，本文考察的是单变量 （单个状态监测变量）情形，多变量情形可参看文献[4]。

在服役样本的第k个采样点，其与参考样本i的相似度为：

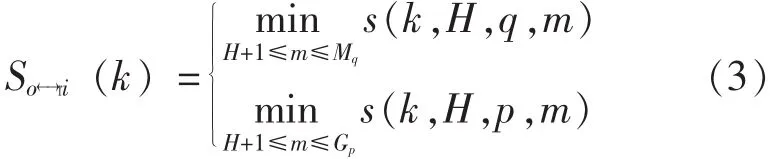
在计算 So←→ri（k） 的过程中，确定 Ni（k） 以满足

根据式 （4），参考样本i在其第Ni（k）个采样点的参考剩余寿命为：

权重函数则是文献 [11]中的权重函数的简单拓展：

其中zi（k）定义为：

式 （7）中，参数α控制了权重分配的方案，增加α的值意味着将更多的权重集中在与服役样本相似度高的参考样本上[17]。权重分配方案对基于相似性的剩余寿命预测方法表现的影响可参看文献[17]。

基于式 （6）中的权重与式 （5）中的参考剩余寿命，服役样本在其第k个采样点的预测剩余寿命为：

式中EMp基于图2或图3中的估计过程予以估计。

作为比较，相应的仅利用失效历史样本的基于相似性的剩余寿命预测方法的预测值如式 （1）所示，且可扩展为：

最后，与文献 [17]中的一样，图3中的总体表现在本文中定义为：

式中 PRLrq（k）、 ARLrq（k）分别为失效历史样本 q 在其第k个采样点的预测剩余寿命和实际剩余寿命。

定义了此总体表现，则基于相似性的剩余寿命预测方法对于服役样本的表现也以此指标考核，即

式 （11） 中，R 为服役样本数， PRLoj（k）、 ARLoj（k）分别为服役样本j在其第k个采样点的预测剩余寿命和实际剩余寿命。一个主要的区别在于式 （10）中的PRLrq（k）是基于剩余 （Q+P-1） 个参考样本预测的，而式 （11） 中的PRLrq（k）是基于全部 （Q+P）个参考样本预测的。

2 数值试验

2.1 仿真数据

本节介绍随机衰退模型，并利用该模型产生参考样本与 （测试用）服役样本的衰退过程以评估1.3节中基于相似性的剩余寿命预测方法的表现。该随机衰退模型已广泛应用于部件剩余寿命的研究中，其最简形式为：

式中，lnθ服从参数为 （μ0，） 的正态分布， β服从参数为 （μ1，） 的正态分布， ε（t）服从参数为 （0，σ2t）的正态分布。文献 [18-19]详细论述了式 （12）的推导过程。

本文中，参照文献 [11]设置lnθ和β的参数，总结如表1所示。

表1 随机衰退模型参数

为确定参考样本与 （测试用）服役样本的实际寿命，进而确定每个采样点其实际剩余寿命，应定义一失效阀值，一旦样本的衰退变量大于该阀值即认为样本失效。本文定义失效阀值L=200。图4演示了3个仿真的衰退过程与失效阀值，其中任意选取的服役样本A（衰退过程加粗线条）的预测剩余寿命将在后文演示。实际衰退过程与图中所示过程类似的有：轴承衰退过程中的振幅[18-19]，BGA封装在随机振动中关键焊点回路两端电压[20]，某激光装置使用过程中的电流[21]，钻头在使用过程中的推力[22]，涡轮蠕变过程的应变量[23]等。可见，所仿真的衰退过程是符合工程实际的。

图4 3个仿真的衰退过程与失效阈值

采用式 （12）中的模型与表1中的参数，仿真了1000组衰退过程，时间范围t=0，1，…，100，△t。在1000组仿真衰退过程中，与文献 [17]中一样，首先任选100个在t=100前失效的样本作为参考样本，另任选500个失效的样本作为服役样本以考察基于相似性的剩余寿命预测方法的表现。此外，再任选20个失效的样本以进一步处理为接受预防维护或终止运行的未失效样本。这将在下一小节予以介绍。

2.2 试验方案与准备

本小节具体阐述数值试验方案，并讨论将20个失效样本处理为未失效样本的方法。

实际中，会有失效历史样本非常有限 （如5个）的情况，也会有存在大量失效历史样本 （如100个）的情况。为全面了解利用失效与未失效历史样本的基于相似性的剩余寿命预测方法的表现，有必要对这些情况做全面的考察。为此，将100个失效参考样本划分为20组，每组5个样本。表2总结了使用不同失效历史样本的基于相似性的剩余寿命预测方法对500个服役样本的总体表现。其中，与文献 [17]一致，采纳参数值α=4，D=10·△t。

表2 使用不同失效参考样本的、基于相似性的剩余寿命预测方法的表现

表2中，PER’的第一列对应于利用第1，2，……，20组失效参考样本时的表现，即基于相似性的剩余寿命预测方法的参考样本数为5；PER’的第二列对应于利用第1和2，……，19和20组失效参考样本时的表现，即基于相似性的剩余寿命预测方法的参考样本数为10；以此类推。Mean(PER’)为各列PER’的均值。

表2中，容易理解利用不同失效参考样本的PER’会有所不同。此外，随着越来越多的失效参考样本运用于基于相似性的剩余寿命预测方法中，Mean(PER’)逐渐减小，即预测表现逐渐提升。对于每种情况 （即失效参考样本数分别为5，10，20，50），将根据平均表现，比较利用和不利用20个未失效样本的、基于相似性的剩余寿命预测方法。

下面介绍将20个失效历史样本处理为未失效历史样本的方法。首先，基于这20个失效历史样本的PER’计算得13.67，与表2中PER’对应的第3列结果进行比较，显示这些样本并无特殊。为了将20组直至失效的衰退过程转变成被预防维护或终止运行活动所终止的过程，将样本失效前的一部分衰退过程截去。这样做的关键点是截去的衰退过程时间长度。本文，该时间长度定义为：

式（13）中： tr～N（（μ3/5），（σ3/5）2）=N（11.51，6.86）；

μ3——20个失效历史样本的寿命均值；

这样定义Tr的主要考虑是，随着故障预测与健康管理技术的不断发展，我们可以开展基于状态监测的维护时序规划，将预防维护或终止运行安排在接近样本失效的时刻，以充分利用样本的使用寿命。因此，在样本寿命还剩20%左右的时刻开展预防维护或终止运行活动并不是十分困难的。图5演示了3组截断的衰退过程。

图5 三组截断的衰退过程 （用以仿真接受预防维护或终止运行的样本的衰退过程）

2.3 试验结果

本小节给出数值试验的结果。使用方案A和方案B的基于相似性的剩余寿命预测框架的表现总结于表3和表4。表3中，PER’的第一列对应于利用第1，2，……，20组失效参考样本和20个未失效参考样本时的表现，即基于相似性的剩余寿命预测方法的参考样本数为25；PER’的第一列对应于利用第1和2，……，19和20组失效参考样本和20个未失效参考样本时的表现，即基于相似性的剩余寿命预测方法的参考样本数为30；以此类推。Mean(PER’)_A为各列 PER’ 的均值。表4中的各列结果含义相同，只以Mean(PER’)_B表明各列结果的均值是基于方案B取得的。

对于使用方案B的基于相似性的剩余寿命预测框架，使用MATLAB 7.10的广义模式搜索 （generalized pattern search）算法估计EMp。图6演示了基于第一组5个失效样本估计EMp的优化过程。

图6 基于第一组5个失效样本的EMp优化过程，p=1，…，20

图7演示了基于第一组5个失效样本的样本A（见图4）的预测剩余寿命，图中同样给出了每个采样点的实际剩余寿命。图7中，值得指出的一点是当样本实际剩余寿命很少时 （即图7中t=50以后），基于3种方法的剩余寿命预测结果很相近。原因是当接近样本A失效时，样本A与各个 （接近失效的衰退过程被截去的）未失效样本相似度很低，因而在预测样本A剩余寿命时 （根据式 （8））这些未失效样本的贡献很小。

表3 使用方案A的基于相似性的剩余寿命预测框架的表现

表4 使用方案B的基于相似性的剩余寿命预测框架的表现

图7 基于第一组5个失效样本的样本A的预测剩余寿命

图8画出了不同失效参考样本数情况下的Mean(PER’)，Mean(PER’)_A 和 Mean(PER’)_B。基于 PER’的含义，如果 Mean(PER’)＞Mean(PER’)_A，则使用方案A的基于相似性的剩余寿命预测框架表现优于对应的传统方法。对于使用方案B的基于相似性的剩余寿命预测框架也是同样的逻辑。

图8 不同失效参考样本数情况下的Mean(PER’)，Mean(PER’)_A 和 Mean(PER’)_B

图8中的结果，使用方案A的基于相似性的剩余寿命预测框架表现始终优于传统的基于相似性的剩余寿命预测方法，这显示利用未失效样本的益处。当失效历史样本很有限时 （如5个）这样的益处最为显著，而当存在大量的失效历史样本时 （如100个）其益处就不太明显了。另一方面，使用方案B的基于相似性的剩余寿命预测框架在失效历史样本数很有限时 （如5个）表现甚至差于传统的基于相似性的剩余寿命预测方法，但当失效历史样本逐渐增多时其表现迅速提升并最终超越使用方案A的基于相似性的剩余寿命预测框架。这个结果的原因是当失效历史样本很有限时，这些样本无法全面代表服役样本，而优化的EMp仅适用于这些有限的失效样本。当失效历史样本逐渐增多时，这些样本越来越能够代表全体服役样本的特性，因而相应地优化了的EMp的表现提升了。这个发现提示，当失效历史样本有限时采纳使用方案A的基于相似性的剩余寿命预测框架，而在失效历史样本很多时采纳使用方案B的基于相似性的剩余寿命预测框架。

3 结束语

为工程实践所驱使，本文提出一个基于相似性的剩余寿命预测框架以同时利用失效与未失效（由于预防维护或终止使用等）历史样本。在该框架中，提出两种估计未失效历史样本寿命，进而利用其衰退过程信息的方案 （记为方案A和方案B）。一个系统的数值试验验证了在存在有限失效历史样本与存在大量失效历史样本的情况下，基于方案A的框架始终优于对应的传统方法。此外，试验结果揭示基于方案B的框架在失效历史样本有限的情况下并不有效，但随着可获得的失效历史样本的增多其表现迅速提升。

本文强调了利用未失效历史样本的益处。在提出的框架中，所有的失效与未失效样本均予以使用。然而，使用可用的一部分历史样本 （即所有历史样本的子集）是否能带来表现的提升仍是一个开放的问题，而对应的选择机制值得进一步研究。同样地，将基于相似性剩余寿命预测方法推广至非连续监测的衰退过程也是很有裨益的。

[1] JARDINE A K S,LIN D,BANJEVIC D.A review on machinery diagnostics and prognostics implementing condition-based maintenance[J].Mechanical Systems and Sig-nal Processing,2006,20:1483-1519.

[2] HENG A,ZHANG S,TAN A C C,et al.Rotating machinery prognostics:state of the art,challenges and opportunities[J].Mechanical Systems and Signal Processing,2009,23:724-739.

[3] SIKORSKA J Z,HODKIEWICZ M,MA L.Prognostics modeling options for remaining useful life estimation by industry[J].Mechanical Systems and Signal Processing,2011,25:1803-1836.

[4] WANG T.Trajectory Similarity Based Prediction for Remaining Useful Life Estimation[D].PhD Dissertation.Cincinnati:University of Cincinnati,2010.

[5] KAISER K A,GEBRAEEL N.Predictive maintenance management using sensor-based degradation models[J].IEEE Transactions on Systems,Man,and Cybernetics,Part A:Systems and Humans,2009,39:840-849.

[6] YOU M–Y,LI L,MENG G,NI J.Cost-effective updated sequential predictive maintenance policy for continuously monitored degrading systems[J].IEEE Transactions on Automation Science and Engineering,2010,7 （2） :257-265.

[7] YOU M-Y,LIU F,WANG W,MENG G.Statistically planned and individually improved predictive maintenance management for continuously monitored degrading systems[J].IEEE Transactions on Reliability,2010,59:744-753.

[8] YOU M–Y,MENG G.A generalized similarity measure for similarity-based residual life prediction[J].Proceedings of the Institution of Mechanical Engineers,Part E:Journal of Process Mechanical Engineering,2011,225:151-160.

[9] ZIO E,MIAO F D.A data-driven approach for predicting the remaining useful life in dynamic failure scenarios of a nuclear system[J].Reliability Engineering and System Safety,2010,95:49-57.

[10] WANG T,YU J,SIEGEL D,LEE J.A similarity-based prognostics approach for remaining useful life estimation of engineered systems[C]//Proceedings of the International Conference on Prognostics and Health Management.2008.

[11] GRBRAEEL N,LAWLEY M,LIU R,PARMESHWARAN V.Residual life predictions from vibration-based degradation signals:A neural network approach[J].IEEE Transactions on Industrial Electronics,2004,51:694-700.

[12] BONISSONE P,VARMA A,AGGOUR K.A fuzzy instance-based model for predicting expected life:A locomotive application[C]//Proceedings of the IEEE International Conference on Computer Intelligence and Measurement System Applications.2005.

[13] HUANG R,XI L,LI X,et al.Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods[J].Mechanical Systems and Signal Processing,2007,27:193-207.

[14] XUE F,BONISSONE P,VARMA A,et al.An Instancebased method for remaining useful life estimation for aircraft engines[J]Journal of Failure Analysis and Prevention,2008,8:199-206.

[15] TIAN Z,WONG L,SAFAEI N,A neural network approach for remaining useful life prediction utilizing both failure and suspension histories[J].Mechanical Systems and Signal Processing,2010,24:1542-1555.

[16] SAXENA A,GOEBEL K,SIMON D,EKLUND N.Damage propagation modeling for aircraft engine run-to-failure simulation[C]//Proceedings of the International Conference on Prognostics and Health Management.2008.

[17] 尤明懿.基于相似性的剩余寿命预测：鲁棒性与不确定性研究 [J].电子产品可靠性与环境试验，2011，29（6）： 10-18.

[18] GEBRAEEL N,LAWLEY M A,LI R,et al.Residual-life distributions from component degradation signals:A Bayesian approach[J].IIE Transactions,2005,37:543-557.

[19] GEBRAEL N.Sensory-updated residual life distributions for components with exponential degradation patterns[J].IEEE Transactions on Automation Science and Engineering,2006,3:382-393.

[20] YOU M–Y,LIU F,MENG G.Benefits from condition monitoring techniques:A case study on maintenance scheduling of ball grid array solder joints[J].Proceedings of the Institution of Mechanical Engineers,Part E:Journal of Process Mechanical Engineering,2011,225:205-215.

[21] MEEKER W Q,ESCOBAR L A.Statistical methods for reliability data[M].New York:John Wiley&Sons.Inc.,1998.

[22] KIM Y S,KOLARIK W J.Real-time conditional reliability prediction from online tool performance data[J].International Journal of Production Research,1992,30:1831-1844.

[23] SWINDEMANA R W,SWINDEMANB M J.A comparison of creep models for nickel base alloy for advanced energy systems[J].International Journal of Pressure Vessels and Piping,2008,85:72-79.