基于情境法的投资策略及其实证*

2012-03-19易秀英王三宝

湖北理工学院学报 2012年3期

易秀英王三宝

(湖北理工学院师范学院，湖北黄石435003)

0 引言

大多数投资者进行投资组合时考虑2 个目标:一是获得较高利润;二是承担较低风险。处理这 2 个目标问题最常用的方法是Markowitz 法。1952年，美国经济学家、金融学家、诺贝尔奖获得者哈里·马科维茨(Harry Markowitz)的“资产组合选择”一文发表，标志着现代资产组合理论的诞生。该文创立了用风险资产的收益与风险之间的关系来讨论不确定性经济系统中最优投资组合的选择问题，其核心是均值－方差准则，即M/V 准则。

证券投资组合是投资者对各种证券资产的选择而形成的投资组合。由于证券投资收入受到多种因素的影响而具有不确性，人们在投资过程中往往通过分散投资的方法来规避投资中的系统性风险和非系统性风险，实现投资效用的最大化。

证券投资是投资者比较普遍的行为，其未来收益也是不确定的，证券投资收益的不确定性成为证券投资的风险，风险的大小取决于不确定性方面的客观和个人主观方面因素，实际度量风险时我们仅考虑证券本身的收益不确定性，在此背景下，投资环境和Markowitz 的投资组合理论为投资者提供了决策指导。

1 Markowitz 均值－方差模型

设一个投资组合具有n 个证券，对于给定的持有期，其平均收益率分别为R1，R2，…，Rn，投资组合的期望收益率为。投资者面临的一个重要问题是如何对每个证券分配适当的投资权重wi(i =1，2，…，n)，从而使投资者能够达到收益较高同时风险较低的投资目标。用方差σi反映第i 个证券的风险，协方差σij反映第i 个证券与第j 个证券的线性相关程度(i，j = 1，2，…，n)，则方差反映了投资组合的风险［1］。

1.1 投资环境假设

现给定如下假设:

1)证券市场是有效的，证券的价格反映了证券的内在价值，每个投资者都掌握了充分的信息，了解每种证券的期望收益率及标准差，不存在交易费用和税收，投资者都是价格接受者，证券是无限可分的，必要的话可以购买部分股权。

2)投资者是厌恶风险的。

3)投资者将基于收益的均值和标准差或方差来选择最优投资组合，如果要他们选择风险(方差)较高的方案，他们都要求有额外的收益作为补偿。

4)所有wi是非负的，即不允许买空与卖空。

1.2 投资策略模型

为使投资组合达到一定收益率水平且风险最小化，采用如下有约束条件的非线性规划模型(Markowitz 均值－方差模型)［2］:

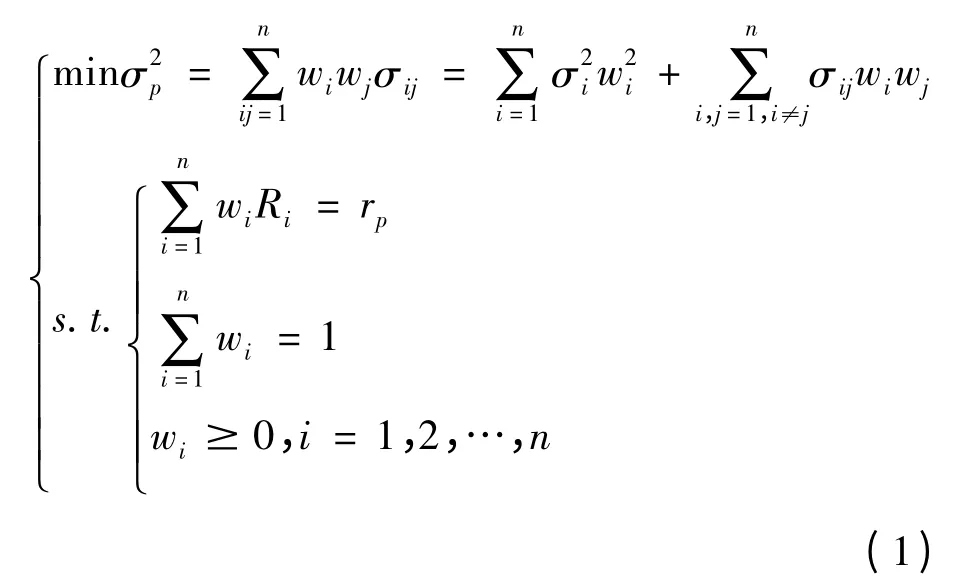
1.3 情境法

投资组合优化问题中的一个重要问题是评价作为决策工具的数学模型是否有效，然而模型的有效性又与模型求解所需的数据以及生成这些数据的方法有着密切的关系，这些生成数据的方法被称为情境生成方法。本文主要讨论的是历史数据法，由于不需要对收益分布函数进行任何假设，并且简单易行，历史数据法在情境生成时得到了广泛的应用。这一方法基于假设“历史数据有可能是未来情境的表现”，并且通常情况下假设每种情境都可能发生，这种方法保持收益率的历史均值和方差不变，其缺点是当前价格的未来变化与历史观察不同时，就不能准确反映未来收益率的变化，同时由于历史数据的可得性，对于情境生成的样本数量有所限制［3－4］。

2 仿真与实证

2.1 实证

基于情境法，我们采撷了2005年8 月至2010年9 月60 个月的收益率数据(表1)，考察广电电子(gddz)、盘江股份(pjgf)和长电科技(cdkj)3 只股票。参考当时我国2005年－2007年纸质凭证式国债，其利率在3.8%左右。购买这类国债不失为一种既安全、又灵活、收益适中的投资方式，它是集国债和储蓄的优点为一体的投资品种，可作为无风险资产投资。

仿真基于均匀分布，在Mathematica7.0 环境下，按以下步骤进行:

1)假设12 个月中的每一个月成为上述60 个月之一的概率相等，对每只股票生成12个月的月投资收益率，计算其年度投资平均收益率(以2005.8.30 为基准价);年度投资平均收益率= (年末价格－年初价格)/年初价格，年初价格即第1 月初价格，年末价格即第12 月末价格。

2)对每只股票生成1 000 个次年(2011年)年度投资平均收益率的样本。

生成1 000个样本后的年度投资平均收益率算法如图1所示。

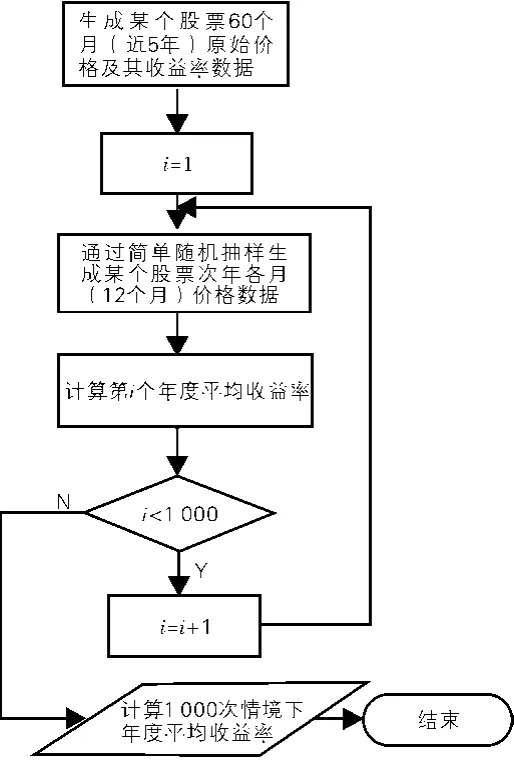
图1 生成1 000 个样本后的年度招资平均收益率算法程序

仿真过程将生成次年投资各股票的年度期望收益率(表2)、风险(方差)－年度期望收益率(表3)及其散点图(图2)等。其中表3的结果来自于式(1)，在Mathematica7.0 环境下［5］，依照微分进化算法，对Markowitz 均值－方差模型实施有约束条件的非线性规划问题求解而得到，结果如下:

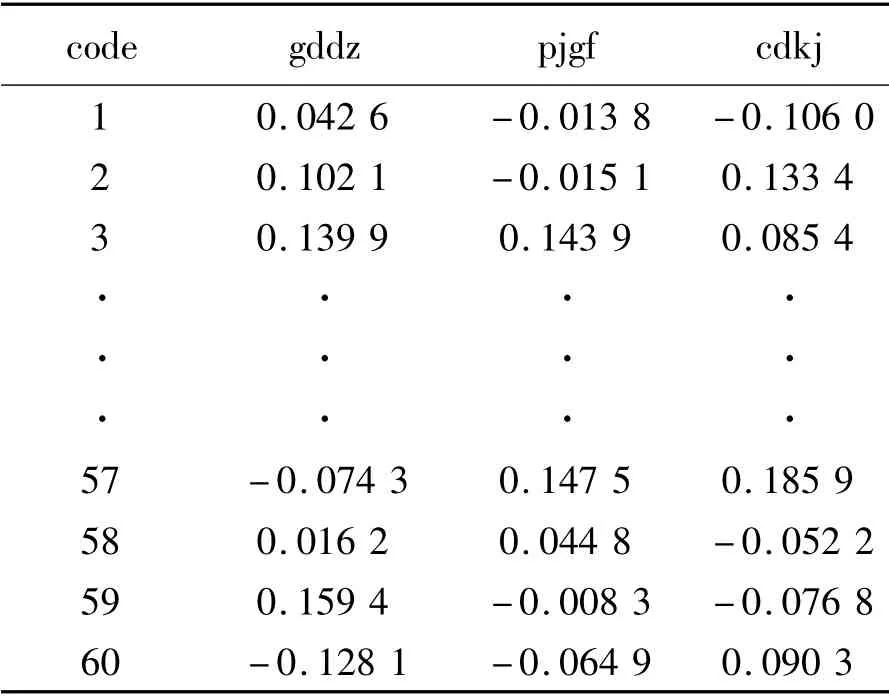
表1 2005.8.30－2010.9.30 3 只股票60 个月的月收益率

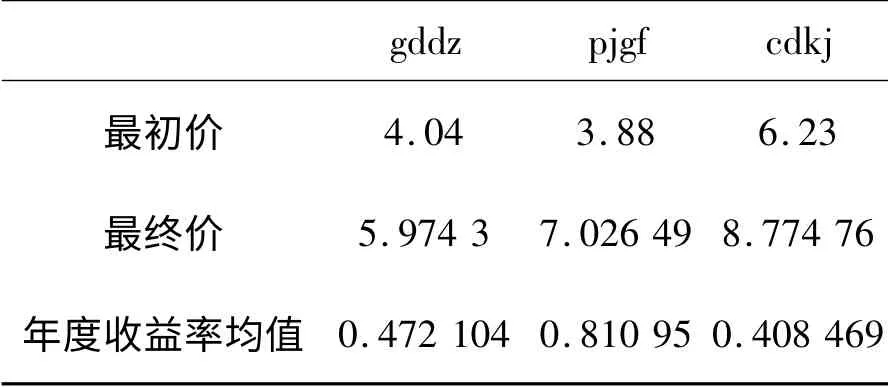
表2 年度期望收益率

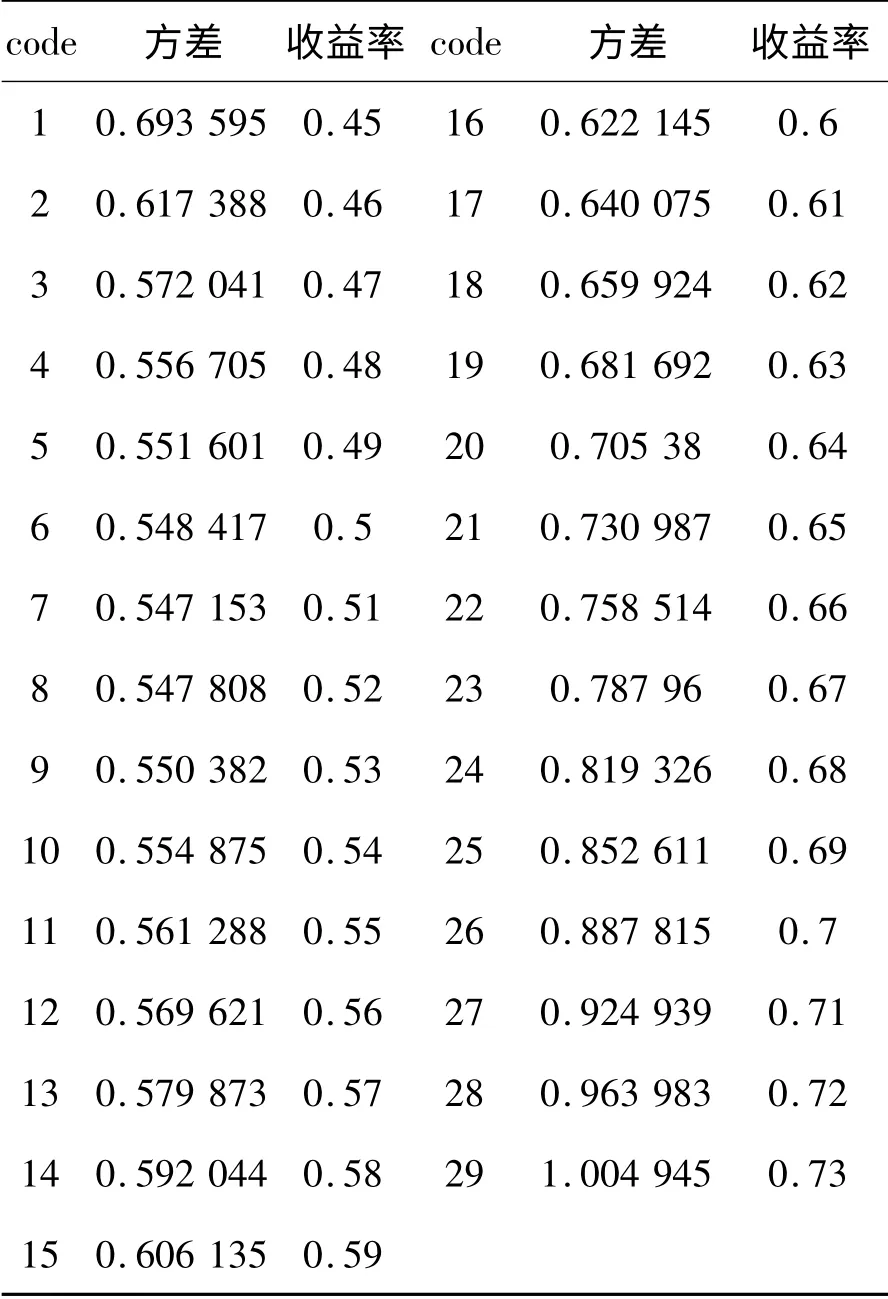
表3 风险－年度期望收益率

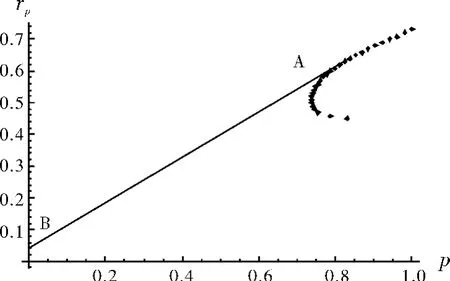
图2 加入无风险资产后投资组合的方差－年度期望收益率散点图

2.2 仿真分析

表3 和图2 显示，投资组合的期望收益率越高，其风险越大，高收益对应高风险。在这3 只股票中，按表3 中的第12 个或第13 个方案进行投资组合，将投资比例向量分别确定为{0.34，0.22，0.44}或{0.32，0.25，0.43}，这时其风险分别约为0.569 6 和0.579 9，风险和收益相当。在其他情形下，投资者都将承担较大风险。显然这3 只股票是高风险和高收益的品种。

首先，从表3 的计算过程得知:组合投资可以将风险分散，单个资产风险会在组合风险分散的效力下消失，不同股票间的相关系数是进行投资组合应考虑的主要因素。

我们不妨构建一个等比例的资产组合，即每一资产有平均的权重wi= 1/n，则组合的方差为:。式中第1 项是各项资产自身方差项对组合风险的贡献，它反映了每一资产本身的风险状况对资产组合风险的影响;第2 项是各项资产间的相互作用，即协方差项对组合风险的贡献。

考虑分散化的影响。当n 足够大时，第1项趋近于0，第2 项接近于平均协方差，即组合风险只包含了平均协方差。这表明资产特定风险可以被分散掉，也就是说，组合风险分散所能达到的最低风险是组合内所有资产的平均协方差，个别资产的总风险将会在组合风险分散的效力下消失，最重要的是考虑不同资产间的相关系数。

其次，由式(1)可知，每项资产投资的比例、方差以及它们之间的相关系数都会影响到整个投资组合的风险。如果假定投资组合的期望收益为一常数，资产之间的相关性大小将会直接影响其组合风险。在式(1)中，不妨假定n =2，固定收益为rp，则风险为:

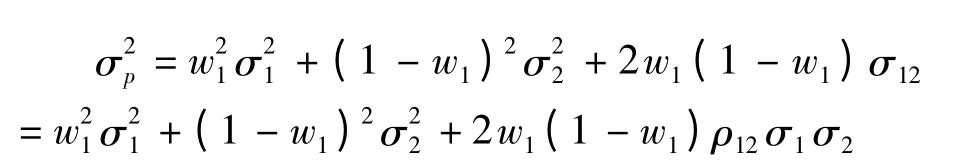
当w1确定，由此可推断:投资组合的期望收益确定后，当投资比例一定时，资产间的相关系数越小，组合风险也越小。从而利用相关性小的资产进行投资组合是降低投资组合风险的有效途径之一。

最后，另外一个降低风险的途径是考虑将无风险资产组合进来。

事实上，假定风险资产组合的收益率为rp，期望收益率为E(rp)，标准差为σp，无风险资产收益率为rf，并假定E(rp)－rf＞0，风险资产的权重为W，则无风险资产的权重为(1－W)，记这样的一个组合为C，则其期望收益率与风险如下:

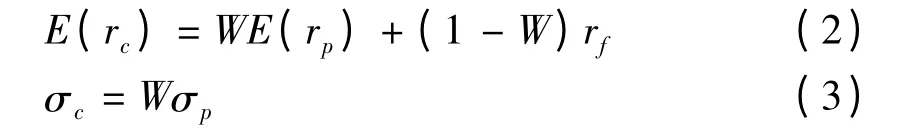
由式(2)显然有:σc＜σp

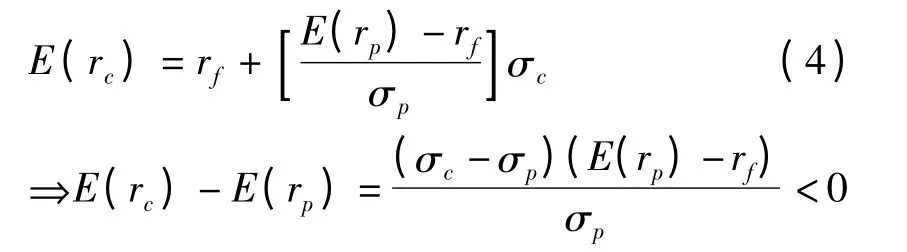
其中式(4)由图1 中的AB 直线所示，我们称其为资本配置线［6］，A 点代表风险资产，它是连接rf点(即B 点)和A 点的直线方程，也表示了投资者对风险资产和无风险资产任一分配比例所构成的组合，一定位于这条直线上;反之，资本配置线上的任何一点都代表了某一特定分配比例的风险资产与无风险资产的组合。

加入无风险资产进行组合，对风险和期望收益都有所降低。另外，我们还看到，资本配置线的截距为无风险资产的 rf，斜率为，它表示每增加一个单位的标准差会增加的期望收益率，此值越大，意味着直线越陡，即增加单位风险可以增加更多的期望收益，这可理解为资产配置线与风险资产投资组合的方差－年度期望收益率散点图形成的曲线相切，切点A 与rf点(或B 点)的连线理论上应是风险资产与无风险资产所有可行的风险收益最佳组合。

另外，选取较多的投资品种进行组合，也是降低风险的途径之一。