空时交织码

孙 鹏 李道本

(北京邮电大学信息与通信工程学院，北京 100876)

移动通信中信道传输条件较为恶劣，发送端传输信号通常经历严重衰落才能到达接收端，接收信号的质量和信息判决的精确率都会剧烈下降.无线传播环境中，调制信号经历复杂的传输路径，从而在时间上形成扩散，即多径.由于信号在时间上的扩散导致了频率上的选择性衰落，多径衰落信道也被称为频率选择性信道.尽管多径信道会引入符号间干扰等问题，但假如不同径的衰落因子相关性较弱，则该多径信道可提供频率分集增益，如加以合理利用，频选信道性能将远高于单径瑞利衰落信道性能.文献［1］证明了随着多径数的增加，系统的性能会逐渐逼近AWGN(Ad-ditive white Gaussian Noise)信道的性能.

多天线的出现则从空间的角度提供了另一维度的分集增益，合理设计发送信号可大幅度提升系统性能，3GPP已经在WCDMA系统中使用了著名的Alamouti方案［2］.近十几年来，已经有多种多样的空时码字提出［2－7］，但大部分的空时码字均是为单径瑞利衰落信道，而未考虑频率选择性信道.实际上，多天线系统的频率选择性信道提供了更多重的分集增益，假如通过合理设计利用该部分分集增益，则系统性能将大幅度提升.LTE等系统中的空频码(space frequency block codes)通过时频转换，直接消除了多径，从而简化了系统设计.但该方法需要以OFDM(Orthogonal Frequency Division Multiplexing)技术为基础，在一些OFDM不适用的场合，比如一些对峰均比(peak to average power ratio)、移动性、抗干扰性要求较高的系统，该方法就不适合使用.此外，空频码还依赖较强的信道编码获得相应分集增益，当谱效率增加，信道编码码率增高时，系统便不能获得分集增益.因此考虑一般的频率选择性信道中空时码的设计还有很大的意义.

正交的空时码［3－4］可在平坦衰落信道中获得满发分集，但在频选信道中并不能完全利用信道提供的分集.此外，正交空时码还存在码率损失.当天线数大于2时，对于复星座图不存在满分集满速率方案.广义延迟分集GDD(Generalized Delay Diversity)［5］是针对频选信道的主要设计之一，该方案可获得完整的频率分集与空间分集增益.但是随着天线数增加，该方案接收机复杂度指数上升，对系统实现构成了挑战.文献［5］中的简化预编码方案实际是利用IFFT进行时频变换，因此该方案与空频编码面临同样的问题.文献［6］将Alamouti方案推广至多径信道中，但该方案同样存在码率损失.其他满分集满速率方案还有TAST(Threaded Algebraic Space-Time Coding)［7］，该方案的问题则在于接收端复杂度较高，尽管可通过球译码降低，但实际使用中仍然复杂度较高.利用自相关、互相关特性在多径范围内理想的零相关窗码［8－9］也可设计出相应的方案，但谱效率较低，存在速率损失.

本文提出的空时交织码可在多径信道中获得满分集，并进行满速率传输.该方案通过在不同的天线上设置随机交织器获得相应的频率及空间分集增益，因此可应用于任意多根天线.此外，交织器的存在还便于将接收机设计为迭代结构，大幅度简化最优检测的复杂度.仿真结果显示，系统BER(Bit Error Rate)性能在4～5次迭代内便可收敛至理想分集增益曲线，而其复杂度仅仅随发端天线数线性增长.

本文首先介绍系统模型，并给出多径信道下空时码设计的准则.其次给出空时交织码方案及迭代接收机设计方法.最后给出仿真结果及结论.文中各符号含义如下:(·)T表示·的转置;H(i，j)表示矩阵H的第i行、第j列元素;h(i)表示向量h的第i个元素;h［m］表示时变向量h在m时刻的值.

1 系统模型及设计准则

本文主要考虑发端有Nt根天线，收端有1根天线的多入单出(MISO，Multi-Input Single-Output)的系统(但实际上本文所设计方案非常容易推广到多接收天线系统).MISO系统中一般只考虑单码流，该码流经过调制及空时编码从Nt根天线上发射出去.

对于准静态频选MISO信道来说，其等效基带模型可表示为

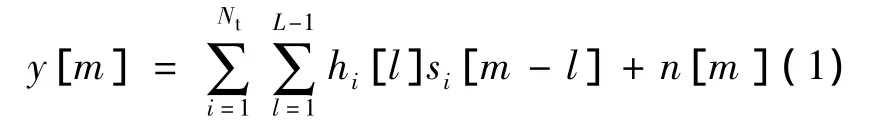
其中，y［m］表示时刻m的等效基带输出;si［ml］表示第i根天线在 m －l时刻的发送信号;hi［l］表示第i根天线与接收天线间多径信道的第l径.本文假设所有Nt根发送天线与接收天线间的多径抽头数目均为L，并且各天线各抽头间分布独立.该模型可表示为向量形式:

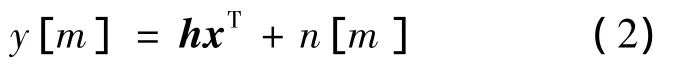
其中

以及

为便于分析，将M个接收符号作为一帧处理，并且前后帧间间隔足够隔离多径影响.定义如下符号向量及矩阵:

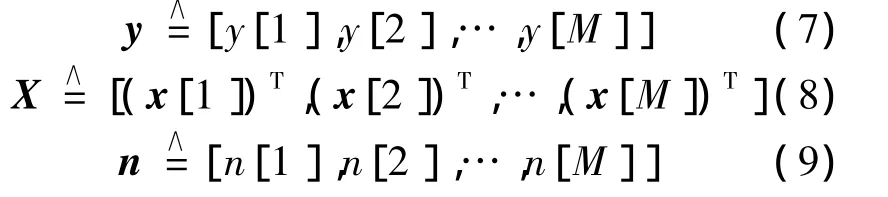
则系统模型可表示如下:

从该模型可看出，Nt根发送天线的频选MISO信道可看作是有NtL根虚拟发射天线，且发送信号按式(8)重组的单径MISO信道.因此单径信道空时块码的满秩准则可推广到多径信道下空时块码的设计.对一预先设计好的空时码，假如发送信号按式(8)重组后的任意两个码字 X(1)和X(2)，其码字差矩阵Xdiff=X(1)－X(2)行满秩，则经接收端最大似然检测便可获得满分集，即NtL重分集.需注意在式(6)、式(8)以及式(10)中，代表时间的变量可能取值为负，这些时刻的各变量取值均设为0，表示在0时刻之前没有信号传输.利用该准则可检查GDD方案.由于天线间的信号有相互L径的延时，因此可以很容易确定按式(8)重组后的码字满足行满秩准字.因此GDD可以实现满分集.

2 空时交织码发射机

空时交织码发射机由同一数据流在不同的天线上进行不同的交织得到，其结构如图1所示.

本文以2根发送天线，2个多径抽头为例说明该设计的有效性.假设发送的调制符号数据流如下:

两根发天线处的随机交织器分别为

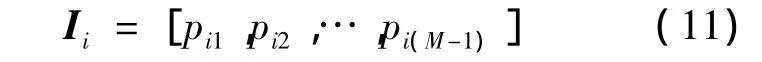
其中pij表示天线i处交织器交织前位置.因此天线i上交织后的数据为

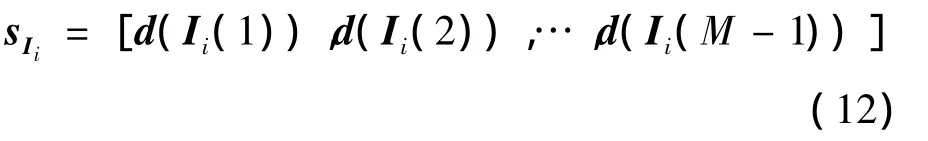
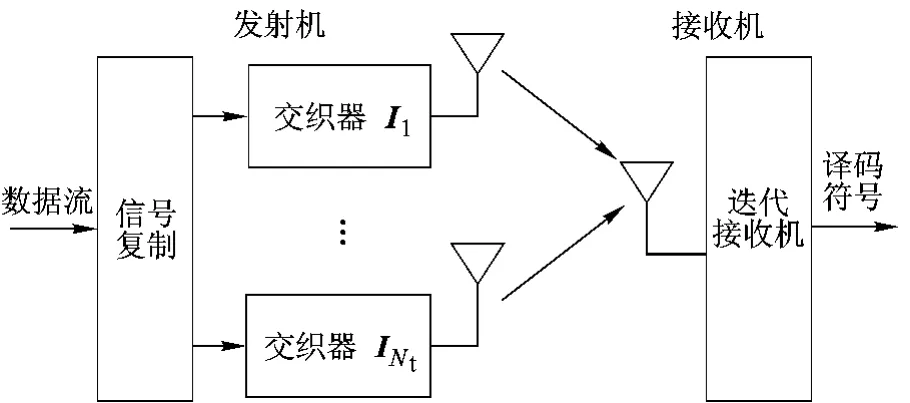
图1 空时交织码系统结构框图

因此两天线上传输数据为

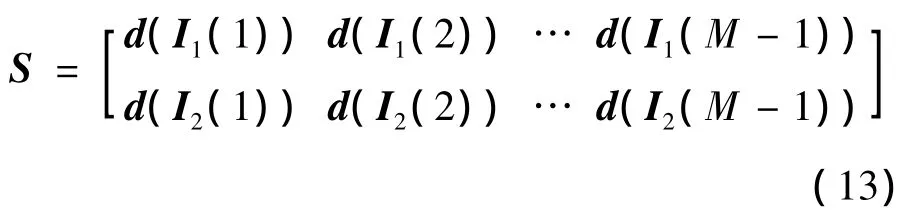
按照式(8)重组可得

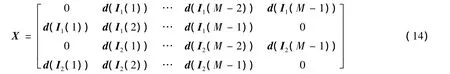
假如系统中未使用信道编码，对应码字差矩阵秩最小的调制符号数据流为仅有一个调制符号不同的两组数据向量.为简便起见，不妨设该不同的调制符号是经天线1处交织器交织后数据向量的第一个，即

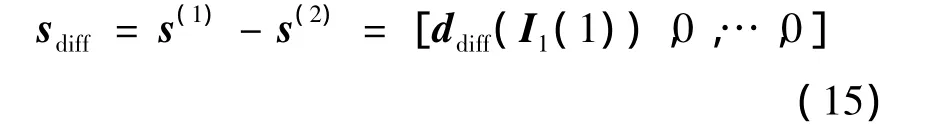
因此重组后的码字差矩阵为

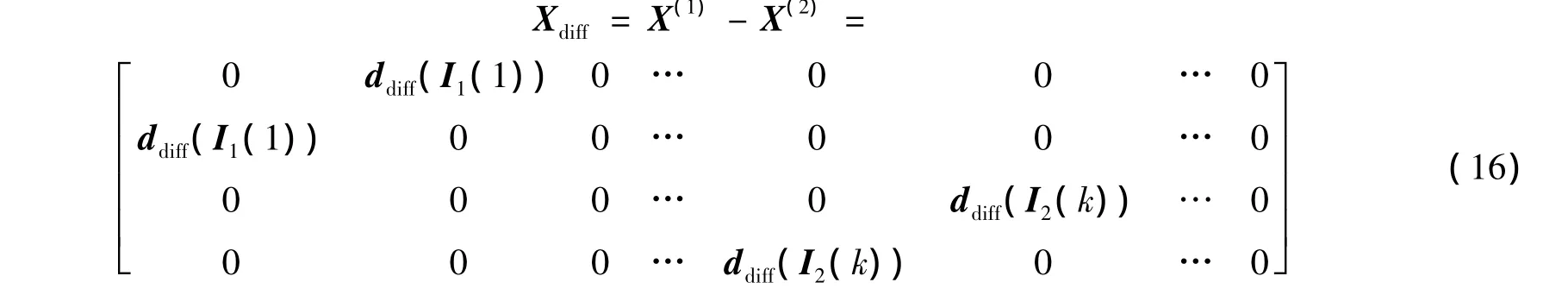
其中

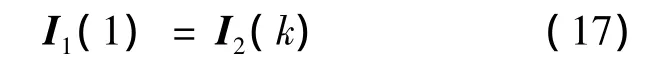
即两交织器分别将原数据流中同一位置的数据交织到位置1处和位置k处.

假如交织器设计合理，可证明码字差矩阵(16)将满足行满秩条件.比如，两天线条件下，S随机交织器将是非常好的选择.该交织器可将一个符号交织到距离之前位置至少一定距离以外，因此式(16)必然满足行满秩.当天线数大于2时，合理设计的行列交织器将满足相应条件.尽管交织器设计看起来比较复杂，但实际上只要数据流长度足够，则在各天线处选择随机交织器几乎以概率1满足行满秩条件.因为对随机交织器来说，产生的随机位置在某范围之内的概率非常小.本文的仿真结果即可证明利用随机交织器进行信号传输已经能够获得非常接近理想性能的结果.

3 空时交织码迭代接收机

空时交织码的最大似然检测如下:

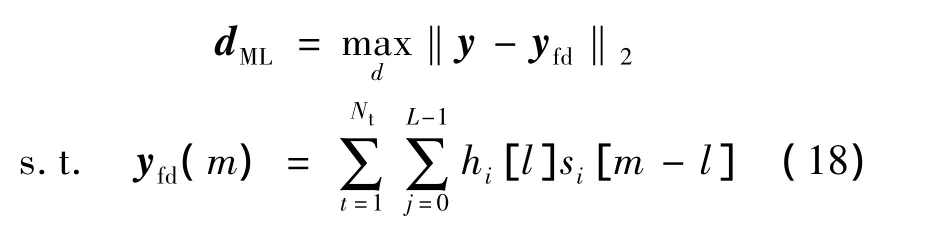
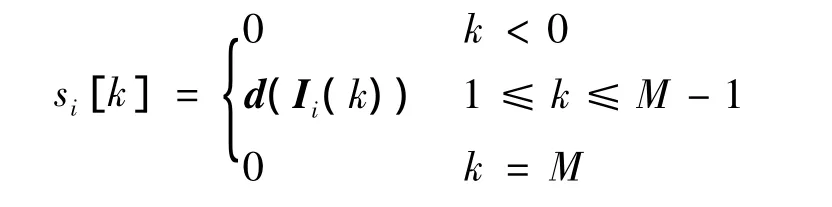
其中，y表示等效基带输出;yfd表示在调制符号数据流为d时接收端未受噪声干扰的衰落信号;si表示天线i处的发送信号.为获得满足上述条件的最优d，整个序列空间都要进行搜索，这一复杂度随序列d的长度指数增长.应当注意到，由于交织器打乱了序列d前后约束关系，维特比算法(VA)并不能在该求解中应用.而在GDD接收机中，由于天线间L符号的延迟可等效为相应的信道延迟，因而可利用抽头为NtL的VA算法求解.尽管相比式(18)，该复杂度可大幅度降低，但其仍然随天线数增加指数增长.

在空时交织码方案中，由于交织器的存在，可以将式(18)中复杂的最大似然接收机分解为若干个软入软出(SISO，Soft Input Soft Output)模块，通过在这些模块之间进行软信息的迭代，可逐渐逼近最大似然检测.可以看到一方面多个天线上的数据是由同一数据流交织得到，因此某些元素相互间满足相等的约束关系;另一方面，多个天线上的数据经过多径信道实际形成了(Nt，1)的卷积约束关系.因此，数据可在这两个约束关系间进行迭代.由于卷积约束关系实际可看作一系列校验关系的串联，即在当前状态、输入信号、下一状态、输出信号间形成校验约束，因此最终的迭代结构实际上是在一组校验约束与一组相等约束间进行迭代，这与(LDPC，Low Density Parity Check)码译码器在校验节点与变量节点间迭代非常相似.

上述(Nt，1)的卷积约束关系仍然较为复杂，其复杂度随天线数增加依然指数上升.因此须对该约束关系进行进一步分解.由于多个天线的数据在到达接收天线前各自经历多径衰落，该(Nt，1)的卷积约束关系可进一步分解为Nt个码率为1的卷积关系的叠加，从而软信息可在叠加的约束关系与Nt个卷积关系间进行迭代.将利用叠加约束关系进行软入软出译码的模块称为解加器(desummer)，其外信息(extrinsic information)计算式为

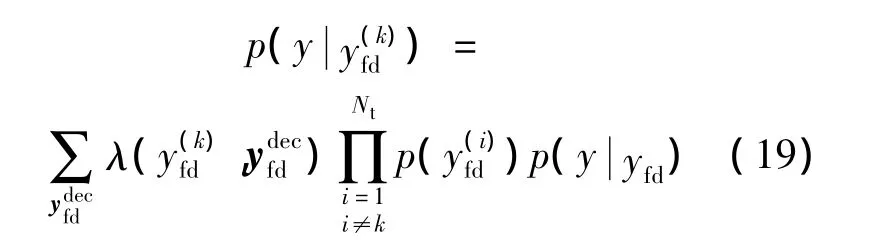
图2 分布式BCJR迭代接收机整体结构图

4 仿真结果

本节通过仿真给出空时交织码及不同接收机结构的系统性能.仿真中各天线各抽头独立同分布，即均服从复高斯分布.仿真中天线数目基本限定在2～8.

首先对空时交织码在频选信道中的有效性进行仿真.发天线数目分别被设置为2，4及8，抽头数量均被设置为2.因此信道提供的多径数量分别为4，8及16.数据流采用 BPSK(Binary Phase Shift Keying)调制.各天线上的交织器为独立生成的随机交织器.接收端采用了图2所示迭代结构，迭代次数为5次.仿真结果在图3中列出.从结果中可看出，该方案性能非常接近理想性能曲线.尽管随着天线数的增加，性能相比理想曲线略有损失，但是可以看到该损失几乎可以忽略不计.此外，尽管由于最大似然检测复杂度非常高而未给出性能，但其应当介于迭代检测与理想分集曲线之间，而仿真显示迭代检测非常接近理想分集曲线，因此最大似然亦应当非常接近理想分集曲线.这也显示迭代检测几乎没有性能损失.同时可见，尽管各天线处采用随机交织器，系统仍然能获得完整的分集增益.

本文还对不同迭代结构性能进行了对比，一种是直接在(Nt，1)的卷积约束关系与相等关系间进行迭代，称之为联合BCJR(joint BCJR)算法，另一种是图2所示迭代结构，称为分解BCJR(decomposed BCJR)算法.仿真中发端天线数为2，多径抽头数为3，仿真各次迭代性能如图4所示.从图中可以看出，尽管联合BCJR算法第一次迭代性能大大优于分解BCJR算法，但随着迭代次数的增加，两个算法间的差距越来越小，最终都收敛于理想分集曲线附近.

图3 空时交织码与理想分集曲线性能比较

图4 联合BCJR与分布式BCJR迭代接收机性能比较

5 结 束 语

综上所述，本文提出了一种新的在频选信道获得满分集满增益的空时编码方案.通过在不同的发送天线处设置随机交织器，该空时码满足了行满秩矩阵，从而能够获得满分集.由于存在交织器的隔离，接收机可在相加关系、卷积关系以及相等关系之间进行迭代，从而使得接收机复杂度大幅度降低.仿真结果显示，频选衰落信道中，空时交织码的误码率曲线非常接近理想分集曲线.因此该方案为多天线系统空时码字设计提供了一个在复杂度和误码率性能方面表现都非常优秀的选择.

References)

［1］李道本.信号的统计检测与估计理论［M］.北京:科学出版社，2004:422－454 Li Daoben.Theory of signal detection and estimation［M］.Beijing:Science Press，2004:422 －454

［2］ Alamouti SM.A simple transmit diversity technique for wireless communications［J］.IEEE JSelect Areas Commun，1998，16(1):1451－1458

［3］ Tarokh V，Seshadri N，Calderbank A R.Space-time codes for high data rate wireless communications:performance criterion and code construction［J］.IEEE Trans Inform Theory，1998，44(2):744－765

［4］ Tarokh V，Jafarkhani H，Calderbank A R.Space-time block codes from orthogonal designs［J］.IEEE Trans Inform Theory，1999，45(7):1456 －1466

［5］ Gore D，Sandhu S，Paulraj A.Delay diversity codes for frequency selective channels［J］.IEEE Proc ICC，2002，3(6):1949 －1953

［6］ Lindskog E，Paulraj A.A transmit diversity scheme for channels with intersymbol interferencee［J］.IEEE Proc ICC，2000，1(3):307－311

［7］ Gamal H El，Damen M O.Universal space-time coding［J］.IEEE Trans Inform Theory，2003，49(5):1097 －1119

［8］李道本.一种具有零相关窗的扩频多址编码方法:中国，CN1321374［P］.2001 －11 －07 Li Daoben.A method of code division multiple access with zero correlation window:China，CN1321374［P］.2001 －11 －07

［9］王雪松，方莉，杨星，等.频率选择性衰落信道中的发射分集设计［J］.北京邮电大学学报，2010，33(6):78 －82 Wang Xuesong，Fang Li，Yang Xing，et al.Design of transmit diversity schemes in frequency selective channels［J］.Journal of Beijing University of Posts and Telecommunications，2010，33(6):78－82

［10］ Bahl L R，Cocke J，Jelinek F，et al.Optimal decoding of linear codes for minimizing symbol error rate［J］.IEEE Trans Inform Theory，1974，20(2):284 －287