用反圆环面刀加工变曲率过渡曲面原理
2012-03-19陈志同陈五一
黄 魏 陈志同 陈五一 贺 英
(北京航空航天大学 机械工程及自动化学院,北京 100191)
过渡曲面用来连接零件上相邻两个曲面,以实现曲面间的光滑过渡.文献[1]认为处理相交曲面在相交棱边处的等半径过渡曲面与数控加工中曲面间过渡区域的生成机理是一致的.事实上,工程中经常遇到变曲率过渡曲面(也称为变半径过渡曲面),它的加工十分复杂.叶片进排气边就是一种变曲率过渡曲面.
叶片是航空发动机中的关键零件,其工作性能对发动机的总体工作性能具有重要影响,而叶片进排气边的形状和精度是决定叶片气动和热传导性能的关键因素之一[2].进排气边曲率半径小、变化范围大,在空间扭曲严重,因此加工难度很大.目前多采用球头刀或圆环面刀按螺旋线扫描方式进行叶片进排气边的精加工,并提出了相应的螺旋线刀轨规划算法[3-5].这些算法的优点是可以实现叶片不同部位的光滑衔接,加工过程中刀轨连续且只需一次进退刀.文献[6]指出刀具的最佳走刀方向应沿着最小主曲率方向,采用螺旋线加工方式很难使叶盆叶背和进排气边同时满足这一要求,而且加工进排气边时,曲面的法矢会旋转180°左右,会导致机床在很大的加速度下做进给运动,不仅会显著降低机床在该区域的插补运动精度,还极易引起工艺系统的颤振.此外由于叶片很薄,厚度方向的切削力使螺旋加工在此处很容易导致叶片变形,并出现过切现象[7].为此,文献[8]提出将进排气边单独加工的方法,该方法使用球头刀沿横向往复加工进排气边,可以解决过切现象,但球头刀加工效率较低.20世纪50年代,前苏联曾采用一种进排气边与叶盆叶背分别磨削的方法[9],这种方法可充分提高各个区域的加工效率,并通过改善支撑系统提高工艺系统刚性.文献[10-11]指出刀具为凸集,没有考虑到凹形刀具在加工凸曲面时的优势.常用的CAM软件也不具备创建凹形刀具的功能.文献[12]最早提出按照曲率吻合原则来规定刀具与工件的相对位置,实现较好的加工效果.根据文献[13]提出的广域曲率吻合原则,如果刀具包络面与工件曲面在每个瞬时接触线上凹凸性相反,并且刀具包络面与工件曲面在每个瞬时接触线上曲率半径尽量相等,则会得到更大的有效行宽.文献[14]也指出,凹半径铣刀非常适合加工至少一个方向为凸的曲面,但是文章并没有提出具体的实现方法和理论依据.因此本文研究反圆环面刀加工叶片进排气边的基本原理和方法,并用最短距离线对原理分析误差分布,为叶片进排气边的精密铣削乃至磨削加工提供一条新途径.
1 凹圆环面刀具加工的几何模型
圆以所在平面内一条与其不相交的直线为轴线旋转一周形成圆环面.以母圆上任意一段圆弧对应的回转面作为刀具工作面,若刀具工作面上任意一点指向空域的法线远离对应母圆的圆心,则称这种刀具为圆环面刀;反之,若指向空域的法线靠近对应母圆的圆心,则称这种刀具为反圆环面刀.
图1a中,Sw和St分别为工件设计曲面和刀具工作面,二者相切于工件设计曲面上的p点.如图1b所示,在笛卡尔坐标系中,St1(xt1,yt1,zt1)为原点位于刀具底部中心的刀具坐标系,Ta,Tc分别为刀具的刀心矢量和刀轴单位矢量,Γ为xt1-zt1坐标平面第1象限上的圆弧母线,q0为母线上一选定点,其在St1上的坐标为分别为该点的单位切矢量和单位内法矢量,t为与刀轴矢量T的夹角.以q为坐标系原点,以a0轴,为 zt2轴建立刀具局部坐标系.设 q1为刀具母圆上任意点,该点与xt1轴的夹角为α,q2为q1绕zt1轴旋转β所得到的刀具曲面上的任意点.刀具的几何参数如图1b所示,刀具外半径为R,母线圆弧半径为r,张角为φ,圆弧母线下端点距刀具底面距离为h0.
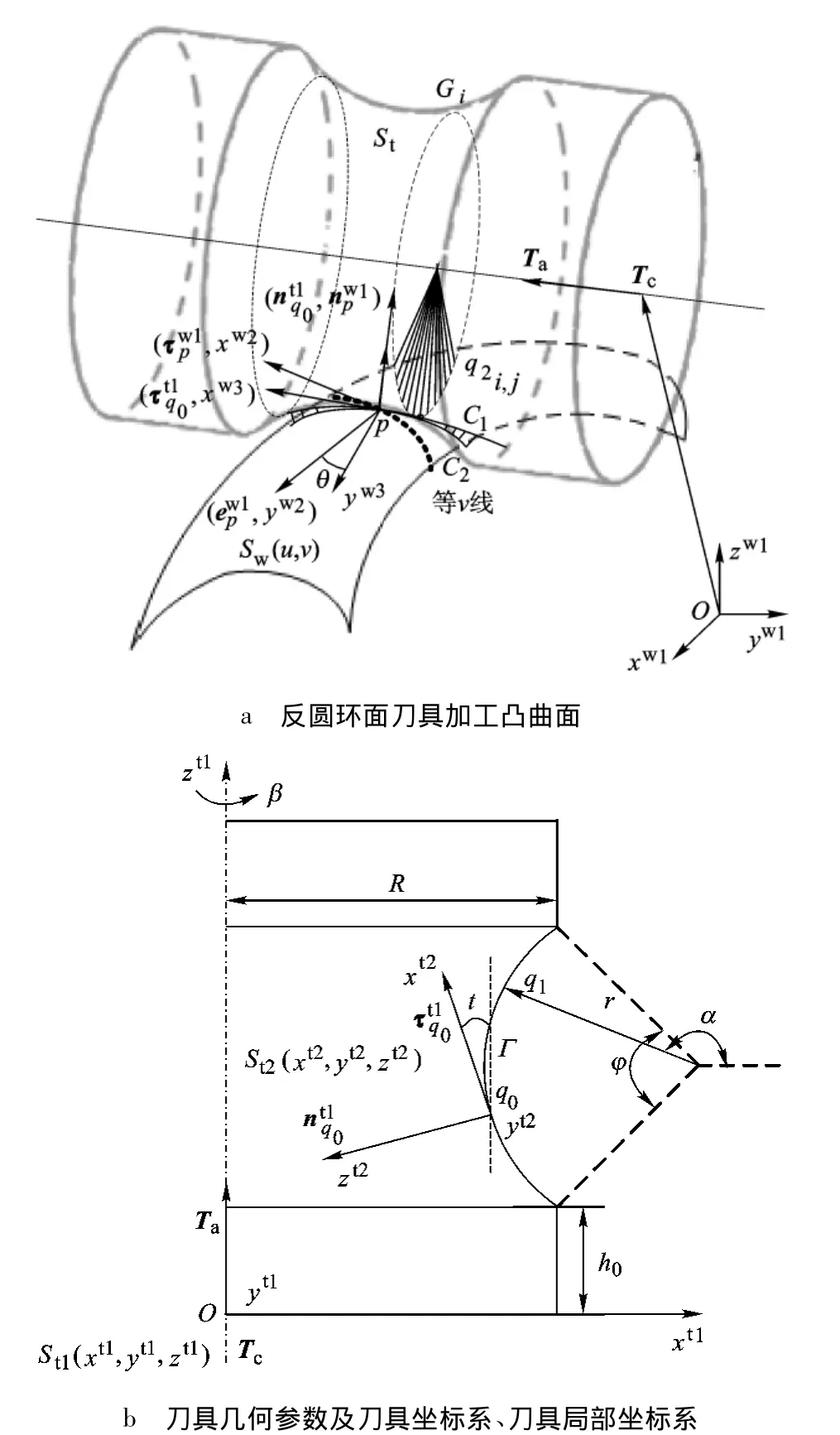
图1 刀具和工件的接触状态及基本定义
如图1a 所示,设 Sw1(xw1,yw1,zw1)为工件坐标系,设为曲面Sw上点p沿进给方向的单位切矢量为p点的单位法矢量,令则构成 p点的工件局部坐标系.令 Sw2绕旋转 θ得到工件局部动坐标系 Sw3(xw3,yw3,zw3).St2与 Sw2重合即可得到一个刀位.
2 刀具及其位姿的表达
2.1 刀具上一点在S t2上的表达
根据图1b,刀具上任意点q2的坐标为
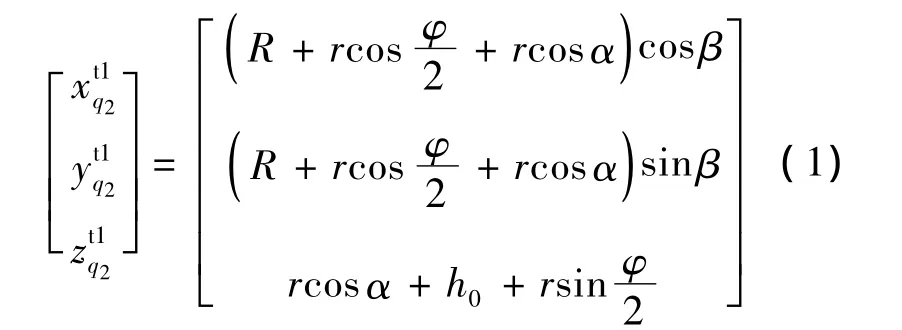
利用坐标变换可求得点q2在St2下的坐标为
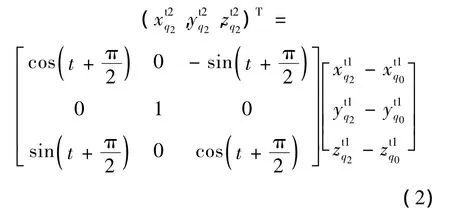
2.2 刀具上点及刀具位姿在S w1上的表达
令St2与 Sw3重合,根据 Sw1中的矢量,容易得到刀具上一点q2在Sw3上的表达为

根据式(3),刀具的位姿可用Tc和Ta在Sw1下的坐标唯一表示成
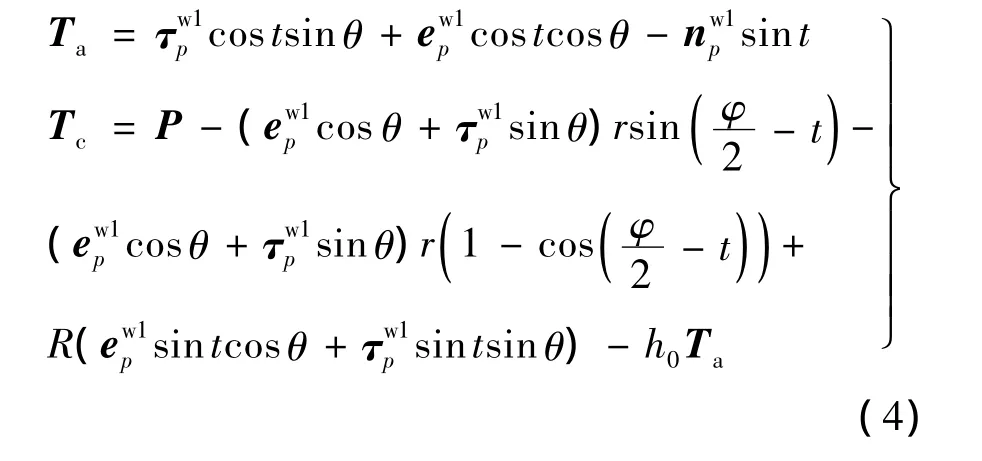
3 反圆环面刀具宽行加工的原理
定半径圆弧母线刀具沿直线或空间曲线作平移与旋转的复合运动时其包络面的截形不断变化,因此可以使刀具包络截形的曲率半径接近任意位置工件截形的曲率半径,从而大幅度提高加工效率.
下面进行简要证明.设工件曲面为半径为r'(r'< r)的圆柱面,其轴线沿 Sw1(xw1,yw1,zw1)的yw1轴方向;刀轴矢量位于y-z平面内,刀具相对zw1轴摆角θ后刀具与工件相切于p点,且切点沿yw1向运动,现推导其包络面方程.
如图2所示,刀具工作面上任一点q0的外法矢量为
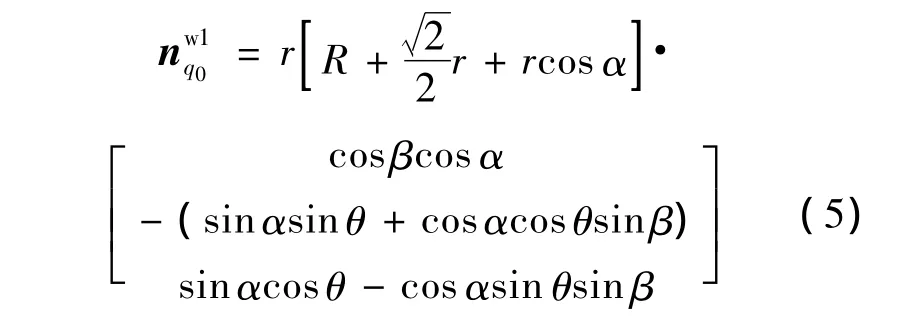
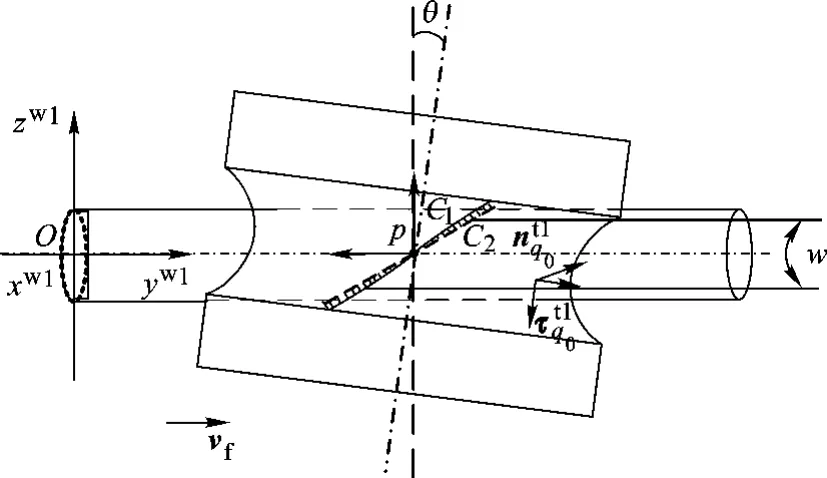
图2 反圆环面刀具与圆柱工件表面的包络关系
刀具上任意点沿yw1轴正向移动,则各点的运动速度方向为
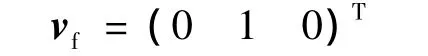
根据包络理论应有
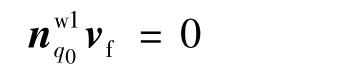
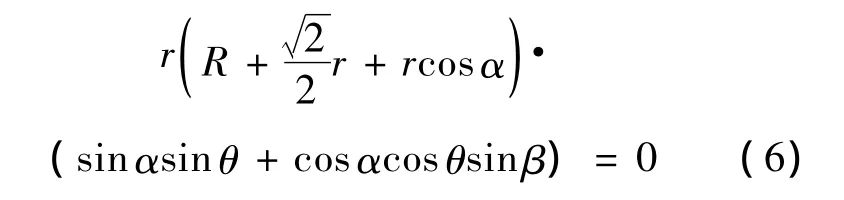
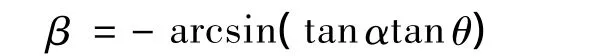
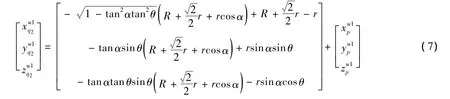
图2所示的曲线C1即为式(7)所描述的St1下的刀具工件啮合特征线,而C2为C1到工件曲面距离最短的曲线.它们之间构成了刀具与工件曲面间的最短距离线对.
将式(7)向 Sw1(xw1,yw1,zw1)的 xw1-zw1面投影可得到刀具包络面的正截形,由于平移不改变投影形状和大小,可略去式(7)中p点在Sw1中的位置矢量.可得到
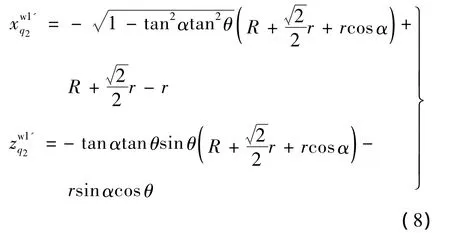
当取 R=5mm,r=1mm,θ=0,5,15,20°时,包络面的正截形和刀具两端截面线如图3实线所示.可见,截型线可以很好地逼近半径分别为1.0,0.96,0.62 和 0.33mm 的圆弧.θ值越大,可逼近的圆弧半径越小.
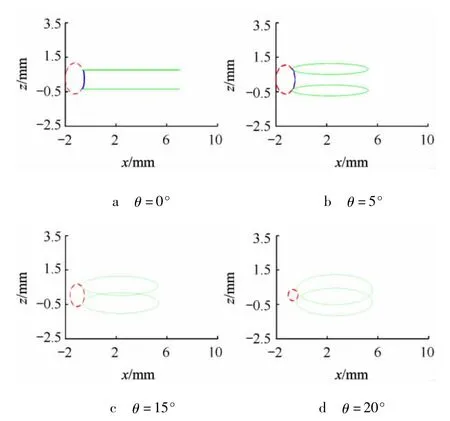
图3 刀具包络面的正截形仿真计算结果
进排气边可以看成锥度不断改变的一个变锥面.根据以上分析结果,利用调整刀具摆角可以实现进排气边的宽行包络加工.
4 刀具参数及刀具位姿的优化模型
4.1 误差分布函数及加工行宽的计算
如图4所示,用M个平行刀具底面的截平面按弧度步长Δφ将刀具工作面划分成M条纬线Gi(i=1,2,…,M),纬线上的点绕刀轴在 Ω 范围内按弧度步长ΔΩ离散成N个点,编号为j(j=1,2,…,N).则离散点可以表示为 q2i,j.求第 i条纬线上到工件曲面上距离最小的点q2imin,并记其在工件上的垂足为pimin.分别连接所有q2imin和所有pimin得到的曲线Ctmin和Cwmin分别称为刀具上的最短距离线和工件上的最短距离线,它们分别是特征线C1和垂足线C2的近似表达.对应点之间的距离分布δimin(i=1,2,…,M)称为误差分布函数δ,即
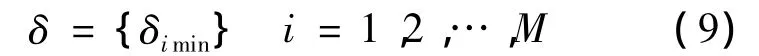
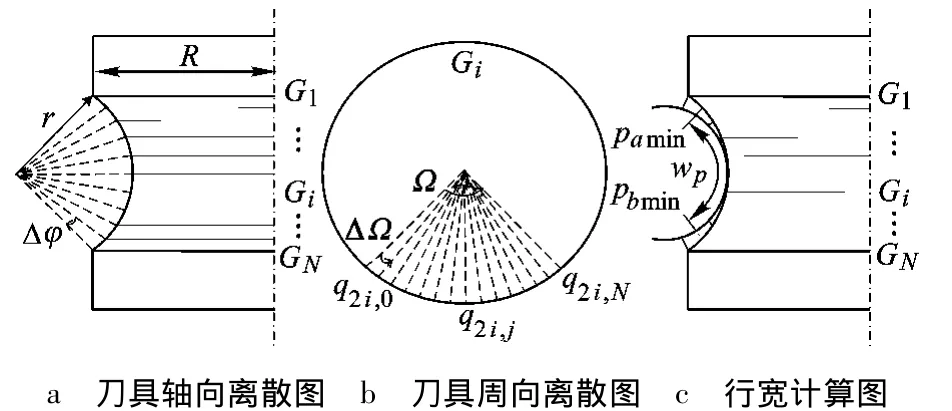
图4 刀具的离散
从切触点q0向两侧各寻找第1个误差大于编程控制误差Δ的点pamin和pbmin,则该刀位上的刀位参数域行宽wp(uv)可表示为
步骤7 标准突变操作。依次判断各栖息地,随机产生Kmu,Kmu∈{1,2,3},若rand
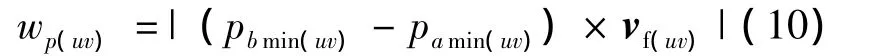
设沿着曲面的参数线走刀,比如u(或v)参数线,则某刀位处误差曲线的两个端点对应工件曲面上点的v(或u)参数值之差的绝对值称为该刀位的参数行宽.
4.2 刀具参数及刀位的优化模型
将满足条件式(10)的行宽称为有效行宽.对于给定的加工曲面Sw和编程控制误差Δ,理论上,给定刀具几何参数时单个刀位点的最大行宽wpmax、给定刀具几何参数时一行刀轨的最大行宽wrmax和优化刀具参数时一行刀轨的最大行宽womax可分别表示为
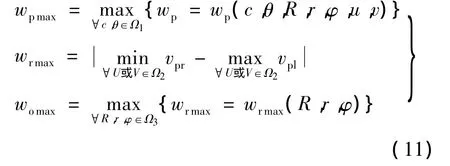
式中,Ω1为刀具与工件不发生干涉时切触点c和摆角θ的范围;Ω2为一行刀轨的u或v参数的离散范围;vpl,vpr为一个刀位处行宽的左右边界;Ω3为刀具几何参数R,r,φ的可取范围.
4.3 刀具几何参数对加工行宽的影响
以某叶片为例,分析了刀具几何参数对加工行宽的影响规律.
4.3.1 r与 womax关系
根据叶片进排气边Sw横截面曲率半径范围Rs∈(0.3mm,1.0mm),显然有 r≥1.0mm.为使刀具工作面与工件曲面更加贴合,取r=1.0mm最为合适.
4.3.2 φ 与 womax关系
刀具工作面应为开敞的曲面,因此弧度范围应满足0<φ≤π.当刀具摆角大于某临界值时,刀具工作面的包络一部分或全部由母圆端点所在的截面线形成,此时不能包络出有效的工件表面,即产生干涉.发生干涉时,包络面的正截形边缘出现自相交,形成封闭区域.
取 r=1.0mm,R=5mm,在 u=0.3 参数线上,计算不同φ值下的最大行宽womax得到图5.
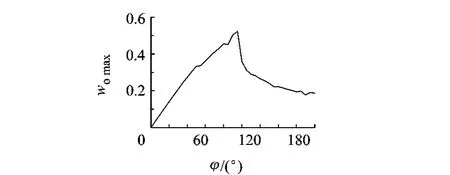
图5 刀具母线圆弧角度φ与w omax关系
由图5可以看出,当φ在90°附近处,womax达到最大值,因此取φ=90°作为刀具母线圆心角.此时womax可超过0.5,因此理论上进气边或排气边只需2行刀轨即可加工完成.当摆角θ变大时可能会发生干涉,而且φ越大,不发生干涉的最大θ角越小.
4.3.3 R 与 womax关系
取 φ =90°,r=1.0mm,沿着 u=0.5 的参数线走刀,在R∈(2mm,30mm)范围内得到的R与womax关系如图6所示.可见,行宽在某值附近波动,而且波动范围很小,womax∈(0.475,0.531),对加工行宽的影响可以忽略,波动是由于离散点计算方式所致.而随着R的增大,摆角θ的临界值逐渐减小.在 u=0.5,v=0.5 处,得到的 R 与最优θ的关系如图6所示.
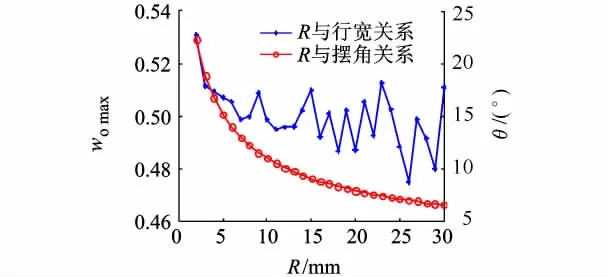
图6 R与 w omax,θ关系
4.4 刀具位姿参数对加工行宽的影响
4.4.1 θ与 wpmax关系
φ取不同值得到的θ与有效行宽womax之间的关系是一致的.在此,取 R=5mm,r=1mm,φ=π/3,c为刀具母线的中点.在 u=0.5,v=0.5 处,得到的θ与wpmax之间的关系如图7所示.
图7中,行宽随|θ|的增大而增大,当大于某一值后,行宽变为0表示发生过切.图7中曲线并不严格关于0°对称,左右极值也不相等,主要是由于进排气边在空间中扭曲所致.有效带宽的最大值发生在有无干涉的临界值附近,因此可以用二分法找到这个临界值作为最优摆角.
4.4.2 c与 wpmax关系
当θ≠0时,由于进排气边的曲面截面线曲率半径变化,刀具与工件间的误差分布在u方向上不对称,因此c应在刀具母线的中点略偏的位置.当取 R=5mm,r=1mm,φ=π/3时,在 u=0.5,v=0.5处,c的位置与加工行宽之间的关系如图8所示.c的最优位置可以通过对母线的中点周围的离散点遍历的方式搜索得到.
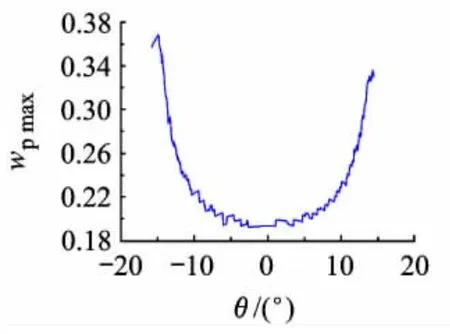
图7 θ与加工行宽的关系
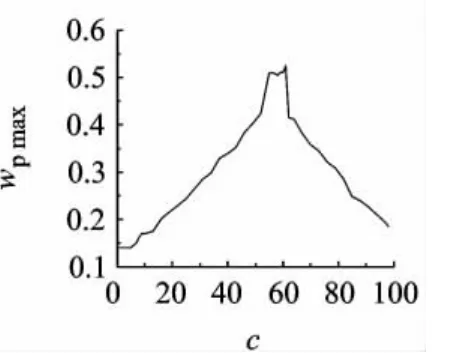
图8 刀具切触点位置c的离散序列与加工行宽的关系
4.5 优化后的刀具几何参数和刀轨生成
根据上述比较结果和验证实验的硬件条件,取R=6mm,根据 Rs范围,取 r=1mm,φ=π/2.
经试算取进气边第1,2行刀轨驱动参数线分别为u=0.27,0.68,两行刀轨有效行宽即可覆盖整个曲面.优化计算后的刀轨如图9所示.如果使用球头刀具加工进排气边,用UG计算需要12行刀轨,因此加工效率比球头刀高5倍.
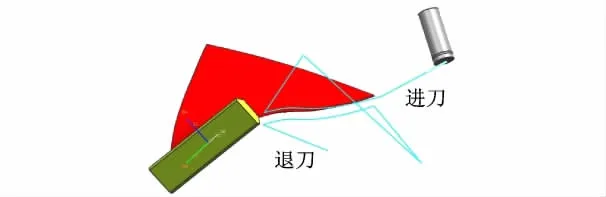
图9 进气边加工刀轨
5 加工验证
实验在3MK5030型五轴机床上用铣削方式进行.叶片毛坯材质为铝.刀具采用整体硬质合金铣刀.切深约为1mm,主轴转速S=3000 r/min,进给速率vf=1 000mm/min.加工后的曲面光滑平整,两行刀轨之间圆滑衔接,如图10所示.

图10 加工后表面质量
在v=0.1与v=0.9处用线切割加工得到的截面形状在显微镜下的观察结果见图11.加工后的进气边圆度较高,与叶盆叶背的连接较好.

图11 加工后截面形状(单位:mm,比例:17∶1)
6 结论
本文提出了一种利用反圆环面刀具纵向精加工过渡曲面的方法,分析了刀具几何参数和位姿对加工行宽的影响规律,提出了刀具几何参数选择的基本原则.利用C语言开发了计算程序.在五轴机床上成功进行了实验.
致谢 本文的研究基于张洪教授最先提出的用反圆环面刀加工变曲率过渡曲面的思想,特此感谢张洪教授对本文的悉心指导.
References)
[1]周济,周艳红.数控加工技术[M].北京:国防工业出版社,2002:46-47 Zhou Ji,Zhou Yanhong.Technology of NC machining[M].Beijing:National Defence Industry Press,2002:46 - 47(in Chinese)
[2] Hamakhan IA,Korakianitis T.Aerodynamic performance effects of leading-edge geometry in gas-turbine blades[J].Applied Energy,2010,87(5):1591 -1601
[3] Kim B H,Choi B K.Guide surface based tool path generation in 3-axismilling:an extension of the guide plane method[J].Computer Aided Design,2000,32:191 -199
[4] Lee E.Contour offset approach to spiral tool path generation with constant scallop height[J].Computer Aided Design,2003,35:511-518
[5] Sun YW,Guo DM,Jia ZY.Spiral cutting operation strategy for machining of sculptured surfaces by conformal map approach[J].Journal of Material Process Technology,2006,180:74 -82
[6] Kruth P,Klewais JP.Optimization and dynamic adaptation of the cutter inclination during five-axis milling of sculptured surfaces[J].CIRP Annals,1994,43(1):443 -448
[7] Shan CW,Zhang D H,Liu W W,et al.A novel spiral machining approach for blades modeled with four patches[J].Internal Journal of Advanced Manufacturing Technology,2009,43:563 -572
[8] You C F,Sheen B T,Lin T K.Robust spiral tool-path generation for arbitrary pockets[J].Internal Journal of Advanced Manufacturing Technology,2001,17:181 -188
[9]伊宗МX.燃气涡轮发动机叶片的机械加工[M].北京:国防工业出版社,1965 Yi Zong M X.Machining of gas twrbine engine blades[M].Beijing:Natinal Defence of Industry Press,1965(in Chinese)
[10] Chiou C J,Lee Y S.A shape-generating approach for multi-axis machining G-buffer models[J].Computer-Aided Design,1999(31):761-776
[11] Yoon Jounghahn,Pottmann Helmut,Lee Yuanshin.Locally optimal cutting positions for 5-axis sculptured surface machining[J].Computer-Aided Design,2003,35:69 - 81
[12]张洪.从增大行距宽度减小波纹度的角度看型面加工发展的方向[D].北京:北京航空学院制造工程系,1982 Zhang Hong.Observing the development of machining sculptured surfaces from the perspective of increasing strip width and decreasing waviness[D].Beijing:Manufacturing Engineering Department,Beijing Institute of Aeronautics,1982(in Chinese)
[13]吕雪丽,张洪.广域曲率吻合原则与复杂曲面数控加工的全面优化[J].机械设计与制造,2003,10(5):94 -96 Lü Xueli,Zhang Hong.Principle of global curvature fitting and global optimization of sculptured surface NC machining[J].Machinery Design and Machining,2003,10(5):94 - 96(in Chinese)
[14] Yu Guang.General tool correction for five-axis milling[J].International Journal of Advanced Manufacturing Technology,1995,10(5):374 -378
