一种基于离散粒子群优化的战场动态频谱指配策略

杨 奎

(中国西南电子技术研究所, 成都610036)

1 引 言

现代战争中,电子装备种类繁多,环境电磁噪声和人为干扰并存,多种因素叠加在有限的战场区域和受限的电磁频谱范围内,使得战区电磁环境非常复杂[1]。需要进行实时的战场频谱管理,而战场频谱管理的一个核心问题便是如何为用频装备动态指配频率,提高频谱资源的利用率[2]。

现有的文献研究中,文献[3]将粒子群算法应用于指派问题的求解,在粒子位置更新时采用了遗传算法粒子交叉的思想,但该算法在应用于较大规模指配时,易陷入局部最优,出现早熟收敛;文献[4]通过改进的粒子群算法求解指配问题,采用处理连续问题粒子群算法的一般公式,在粒子解更新时通过位置的排序来得到新整数排列解,这种做法没有充分考虑到离散型组合优化解的特点,因而会有冗余较大的问题;文献[5-6] 以遗传算法为基础设计了一种战场频率分配算法,但其使用的二进制矩阵编码方式不能够较好地体现问题本身的特征,而且相对应的遗传算子的设计也没有很好地反映搜索空间的结构特点,因此算法不能保证获得最小化相互干扰的分配方案。

本文通过对战场频谱指配主要限制性因素的研究,建立了一种以用频冲突等级最小为基础的频谱动态指配数学模型,将频谱指配问题归结为整个战场用频装备体系的冲突等级评价数学函数的优化问题,并采用一种基于离散粒子群优化算法对其进行分析和求解,能够满足战场频率动态指配实时高效的需求。

2 基于装备用频冲突等级最小的频谱指配模型

战场频率指配问题是指为战区内所有用频装备按需分配频率,并满足一定的约束条件和需求特性。本文主要研究的是区域装备用频冲突最小等级频谱指配问题(M inimum Conflict Grade FAP,MIG-FAP),它属于Fixed-FAP,其优化目标是在指定可用频谱宽度范围的基础上最小化用频装备之间的冲突等级。

2.1 冲突等级

在求解M IG-FAP 时主要考虑两类约束,即站内共址约束(Co-site Constraint,CSC)和站间同频复用约束(Adjacent-area Frequency Reuse Constraint,AA-FRC)[7],其中,CSC 是指为了保证同一站点内的装备之间的正常工作,装备之间应该间隔最小频率距离。AA-FRC 是为了提高频率资源利用率,不同小区(或扇区)可复用统一频率的最小距离间隔。两类约束主要考虑以下3 种要素:

(1)同频冲突等级(Same -frequency Conflict Grade,SFCG);

(2)邻频冲突等级(Adjacent-frequency Conflict Grade,AFCG);

(3)互调冲突等级(Intermodulation Conflict Grade,ICG)。

如果一个用频装备的发射信号落入另一个使用相同频率用频装备的接收灵敏度范围内,则会产生用频冲突,称为同频冲突。设装备A 的灵敏度PR min(dBm)和需求信噪比S/Nmin(dB),针对装备B ,通过电波传播分析模型,分别获得其PRmin-S/Nmin-6、PRmin-S/Nmin、PR min -S/Nmin+3、PRmin-S/Nmin+9 的发射威力分布范围或区域,按照如下设定规则初步判断装备B 对装备A 的用频冲突等级εabi:

(1)装备A 位于PR min-S/N min-6 区域外,返回冲突等级εab0;

(2)装备A 位于PRmin-S/Nmin-6 ～PRmin-S/Nmin区域内,返回冲突等级εab1;

(3)装备A 位于PRmin-S/Nmin～PRmin-S/Nmin+3 区域内,返回冲突等级εab2;

(4)装备A 位于PR min -S/N min +3 ～PR min -S/Nmin+9 区域内,返回冲突等级εab3;

(5)装备A 位于PRmin-S/Nmin+9 区域内,返回冲突等级εab4。

同样,可获取装备A 对装备B 的用频冲突等级εbai。

同理,当装备A 和装备B 采用相邻频率时,在一定条件下(主要针对CSC)将会产生邻频冲突;在Co-site 环境中,一定条件下还将产生互调冲突,在此省略。

在进行战场用频装备频谱指配时,通常可根据装备电磁覆盖方向,结合地理信息系统(GIS)来对用频装备的同频冲突等级、邻频冲突等级和互调冲突等级的系数进行初步构造。设装备i 与装备j 之间的同频冲突等级系数为sij, 邻频冲突等级系数为aij,互调冲突等级系数为hij。

2.2 基于装备间用频冲突等级最小的频谱指配模型

假设作战区域内一共有n 个用频装备,表示为

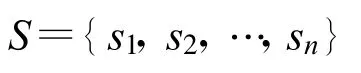
第i 个用频装备可用的频谱数为k 个,则用频装备构成的可用频谱集合可表示为

式中,i =1,2, …, n;k 为第i 个用频装备可用的频谱数。

第j 个用频装备可用的频谱数为l 个,则用频装备构成的可用频谱集合可表示为

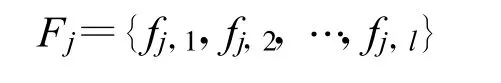
式中,j=1,2, …, n;l 为第j 个用频装备可用的频谱数。

则区域内装备h 可能受到装备i 和装备j 产生的互调冲突的频谱数集合为

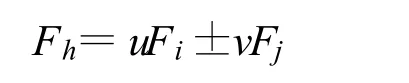
其中, u±v 一般取值为1、3、5、7。

设在[ t,t+Δt]时间范围内,第i 个装备受到第j 个装备的同频冲突等级系数为s＊ij,则有:

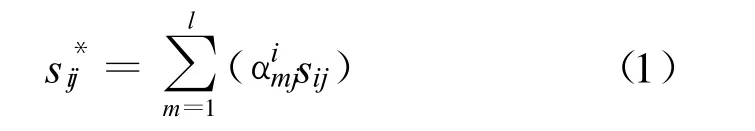
式中,sij为同频冲突等级系数,并有:其中,m =1,2, …,l。

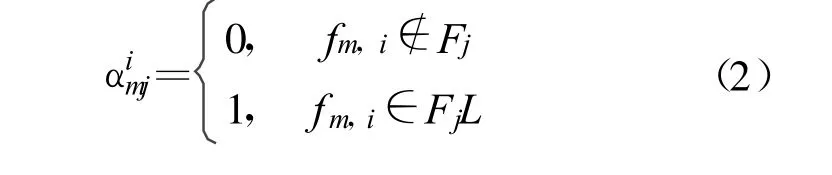
可得,第i 个装备的同频冲突等级系数矩阵为

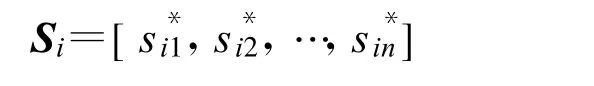
设在[ t, t+Δt] 时间范围内,第j 个装备对第i个装备的邻频冲突等级系数为a＊,则有:

式中,aij为邻频冲突等级系数,并有:

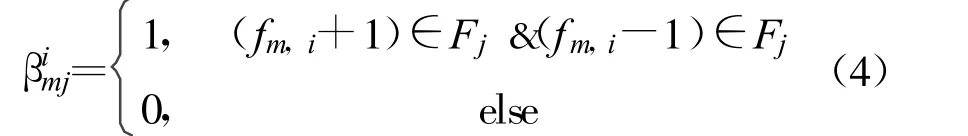
其中,m =1,2, …,l。

可得,第i 个装备的邻频冲突等级系数矩阵为

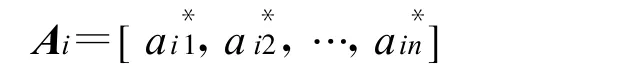
设在[ t,t+Δt]时间范围内,第i 个装备受到装备j 和装备h 产生的互调冲突等级系数为h＊jh ,则有:

式中,hij为互调冲突等级系数,并有:

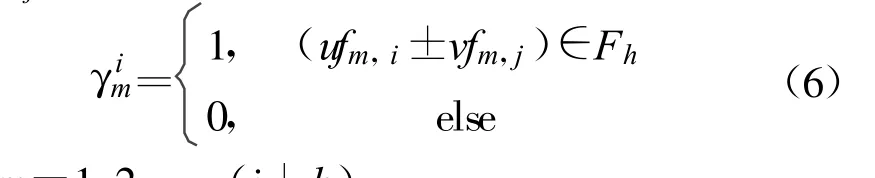
其中,m =1,2, …,(j+h)。

可得,第i 个装备受到装备j 和装备h 产生的互调冲突等级系数矩阵为

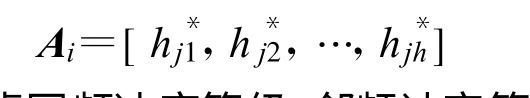
在不考虑同频冲突等级、邻频冲突等级、互调冲突等级相关权重的情况下,可得在[ t, t +Δt] 时间内,区域内其他装备对第i 个装备总的冲突等级系数可表示为

假设需重新对区域内用频装备的频谱进行指配,可将装备i 的全部可用频谱看作变量,将式(7)看作装备i 的用频冲突等级评价函数,则使式(7)的值达到最小就是对装备i 进行频谱指配的目标,从而将频谱指配问题转化为冲突等级评价函数的优化问题。

MIG-FAP 的优化目标是找到一种相互间冲突等级程度最小的可行分配方案,若不考虑频谱指配中的约束条件,通过上述频率分配的数学模型进一步总结优化,整个区域频谱指配的数学模型为

3 基于离散粒子群的指配算法

3.1 离散粒子群优化算法(DPSO)

粒子群优化算法[8]的灵感源于对鸟类捕食行为的研究。基本的PSO 算法中的粒子寻优可用如下两个公式表示:

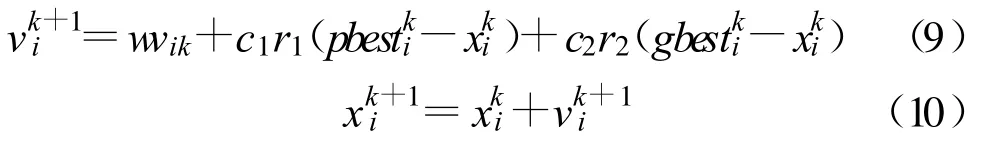
其中,w 为惯性因子;r1、r2是[0,1] 之间服从均匀分布的随机数;c1、c2为学习因子,表示群体认知系数,一般取(0,2)之间的随机数;k 代表迭代的次数;xki为迭代k 次时粒子的空间位置;vki为迭代k 次时粒子i 的速度;pbestki表示粒子本身从初始到当前迭代次数搜索产生的个体极值;gbestki表示整个种群初始到当前迭代次数搜索产生的全局极值。

基本粒子群算法及其改进算法主要用于求解连续性问题。2004 年,Clerc[9]首次对离散问题将粒子群算法的更新公式进行修改,并指出离散粒子群算法(DPSO)的关键是为问题域定义与DPSO 算法相关的数学对象及其运算规则。

3.2 基于DPSO 的频谱指配算法

在文献[6-7,10]的基础上,本文设计了用于求解战场频谱动态指配问题的DPSO 算法。

3.2.1 粒子的编码方式

结合频谱指配问题涉及的要素和特点,设在[ t,t+Δt]周期内,区域内有N 个用频装备,每个装备对应一个频率fi(i =1,2, …,N),个体用正整数序列表示, 代表一种频谱指配方案:f =(f1, f2, …,fN)。我们采用数字符号编码的方式, 即对每一个用频装备个体可用的频谱进行编码,如:可用频谱数为36 个,则第1 个个体的解就是由1 ～36 个正整数组成的,编号按照频率值从小到大的方向进行编码。例如,对于长度为6 的个体,可用频谱对应向量D=(3,11,5,8,1,7)表示用频装备编号为1 ～6 分别对应频谱编号为3、11、5、8、1 和7。

这样,对于一种频谱指配方案,可以编码的方式表示,同时,一种指配方案也可看成是一个粒子。这种编码具有以下优点:一是解码简洁,因为在个体所用频谱与用频装备编号(即频谱指配的解)之间存在简单的一一对应关系;二是清晰,对算法的运算过程便于研究和理解。

因为频谱指配受到同频冲突、邻频冲突、互调冲突以及地理位置等诸多条件的约束,因此,对于每个粒子并不一定能够满足要求的可行解,应在粒子初始化时适当进行调整。

3.2.2 初始化方法

种群中的每一个个体均通过随机的方式生成,根据需求,一个个体的每位数值从相应的频率编号范围内随机选取。为了在粒子群初始化时分散度较好且尽量减少频谱变更的次数,我们利用先验知识指导初始化过程,即初始化时尽量保证每个装备的频率编号各不相同(首先尽量排除同频冲突);其次,相邻装备之间频率编号间隔尽量选择较大(尽量排除邻频冲突),并在初始化分配时,检查互调冲突hij的存在性,形成一个可行解,并且在后面的所有操作中,都需保证满足该要求。按照规定数量的粒子要求进行重复构造,得到初始粒子群。

3.2.3 适应度函数

在评估个体适应度时,首先需要根据输入的用频装备的数目、用途、工作模式等需求对个体进行解码,从而获得相对应的分配方案,然后根据实际的冲突大小计算该频谱指配方案的冲突等级,即公式(8)中的G。

为了将该问题转换成最大化问题,设xi为一个可行的指配方案,X 为全部可行的指配方案的集合X =(x1, x2, …, xi),我们可以构建下面所示适应度函数:

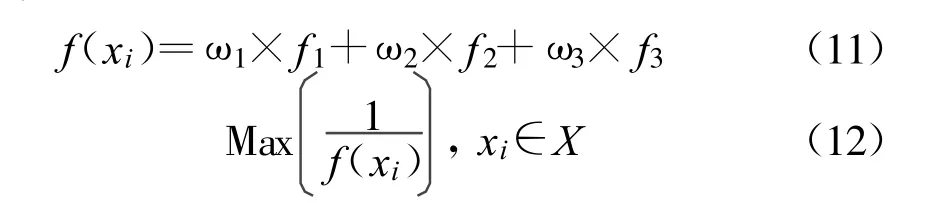
其中, ω1、ω2、ω3为对应的系数权值,其和等于1;f1、f2、f 3分别是满足同频冲突等级、邻频冲突等级和互调冲突等级系数的适应度函数。

3.2.4 粒子位置的更新

为了使得粒子在进行位置更新后所得到的新粒子法新[的1x1ki]操仍中作是交以一叉第种定频位k 谱的代指策的配略第方[i12案 个-13粒,]本。子文我x引 们ki 为入对例一粒进种子行遗位描传置述算更,主要操作流程如下。

(1)xki 首先与gbestki 进行交叉定位操作,产生新粒子Q1与Q2。为使粒子以各种不同的形式以及方向向群体最优解趋近,我们进行粒子与群体最优粒子的交叉操作,具体步骤如下:

首先,在初始可行解向量D 的序列中随意抽取两个位置点,记为P1、P2,且P2大于等于P1,设S1表示xk中从第一个元素至xk中(P1 -1)的元素, S2表示xk中从P2至xk中最后的元素,并用S3表示把pbestk中与S1、S2重复的元素剔除后剩下的元素,最后用Q1表示将S1、S2、S3合在一起构成的新粒子;

其次,设S 4表示pbestk中从第一个元素至pbestk中(P1-1)个元素,设S5表示pbestk中从P 2至xk中最后的元素,并用S 6表示xk中与S1、S 2重复的元素剔除后剩下的元素然,最后用Q2表示将S4、S5、S 6合在一起构成的新粒子。

设有10 个用频装备,可用频谱数为10 个,编号为1 ～10,则交叉的示意图如图1 所示。

图1 粒子的位置更新交叉示意图Fig.1 Cross updating of the particle′s positions

(2)将xk与pbestk进行交叉定位操作,产生新粒子Q3与Q4。为使粒子以各种不同的形式以及方向向个体最优解趋近,将粒子与个体最优粒子进行交叉操作,相应的操作同第1 步。

(3)为了避免粒子运算中陷入局部最优解,对xk进行变异操作,可得到新粒子Q5与Q6。变异操作需要首先在可解码的空间中随机生成一个新粒子Qnew,然后再将Qnew与xk进行交叉,相应的操作同第1 步。

(4)通过计算得到粒子Q1～Q6的适应度分别为f 1-f 6,我们选择其中最小适应度的粒子Q min,并用Qmin去更新pbestki和gbestki。若Qmin的适应度f min小于pbestki,则pbestki+1等于Qmin;若f min小于gbestki,则gbestki+1等于Qmin。

3.2.5 局部搜索策略

PSO 算法在寻找全局最优时容易陷入局部最优解,即出现早熟收敛的问题。因此,为避免粒子陷入局部极值,可以适当通过将粒子的多样性增加,使粒子能够跳出局部最优。本文采用一种基于粒子群局部的搜索策略,改进3.2.4 节中位置更新后的粒子xk,主要的方法是:基于粒子位置的向量长度,选取若干对随机位置点,再交换每对位置点的值,可得到作为下一次迭代是新的粒子位置xki+1。如对一个向量长度为10 的粒子进行局部搜索,我们选取两对随机位置点,同时交换两对随机位置点的值,即得到新的粒子位置,如图2 所示。

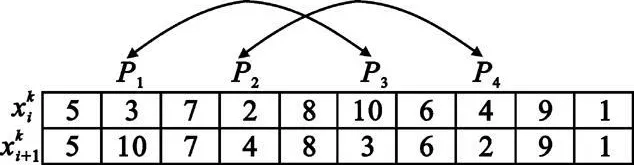
图2 粒子的局部搜索策略Fig.2 The searching policies of particle

也可随机从6 个新粒子Q1 ～Q6中选择1 个作为下一次迭代的粒子位置xki+1。实验证明,采用局部搜索策略可以增加粒子群解的多样性,使算法运行不容易出现早熟收敛而陷入局部最优解。

4 仿真分析

算法使用C++编码实现,平台环境为Windows XP Professional SP3 操作系统,开发环境为Microsoft Visual Studio 2010 ver10.0.30319.1 RTMRel。

设区域内有30 个台站,每个台站内有1 ～3 台用频装备等到指配频率,即种群大小为N=30。装备之间的限制关系已知,设可使用的频谱数为90个,分别表示为f1、f2、f3、…、f90,则可用如下方法进行初始指配:分别取F1 =f 1, f 31, …, f61、F2 =f 2,f32, …,f62、…、F30=f30, f60, …, f90,这样即完成30组不同频谱向不同用频装备的初始指配,因此,台站内部可避免同频冲突的限制。而对于用频装备之间的邻频冲突、互调冲突等,需要基于相关用频分析算法将冲突的约束数降到最低。

测试时,台站数目分别设为20、40 和60,且均是从某区域内的实际用频装备站中随机选出的站点。可分配的波道按照频率从小到大依次编号为1 至200,且预设每个台站统一配置3 个用频装备。最终指配结果表明,算法成功找到了满足EMC 的无相互用频冲突的分配方案,从而验证了算法的有效性。若以算法迭代的次数来衡量找到最优解耗费的时间,则当种群数目分别为20、40 和60 时,算法分别迭代了3 次、15 次和26 次找到最优解,说明在有限的频谱情况下,需求频率越多则需要越长的时间找到最优解。算法仿真得到的结果如图3 所示。

图3 仿真结果Fig.3 The simulation result

从图3 中可以看出:

(1)当算法迭代至约50 次时,整个区域的用频冲突等级已趋近最低,可见算法的收敛速度迅速提高;

(2)由于实际工程中,存在各种互调、邻频干扰,要将整个区域内的用频冲突完全消除将是很困难的;从图中可看出,当运行到100 代时,其冲突等级系数仍然达不到0,但可获得[ t, t+Δt]时间周期内区域最小的用频冲突等级,满足最优的频谱指配需求;

(3)通过交叉、变异等离散算法的优化及搜索策略的优化,不但增加了粒子的多样性,避免了陷入局部最优解,同时算法解的收敛速度得到了大大提高,从而进一步提高了离散粒子群算法的搜索效率,且不必设置较多的参数。

5 结束语

本文针对实际战场频谱指配问题,提出了一种基于离散粒子群优化算法的求解方法,算法迭代中采用粒子交叉定位策略,同时引入局部搜索策略更新粒子位置,这样既保证了粒子位置可行性又增加了粒子的多样性,避免了算法早熟收敛、陷入局部最优解。结合实例仿真分析,证明了本文的离散粒子群算法具有较好的收敛性。针对不同的问题实例,将存在最优的参数配置,可将算法的权重系数进行适度的调整,以取得更好的收敛效果,对于参数的优化将在后续工作中进行。

[1] 王汝群.战场电磁环境[M] .北京:解放军出版社,2006:56.

WANG Ru-qun.Battlefield Electromagnetic Environment[M] .Beijing:Publishing Company of PLA,2006:56.(in Chinese)

[2] 王宇飞.无线电频谱分配新概念[ J] .舰船电子工程,2007,27(3):17-19

WANG Yu-fei.A New Method of Spectrum Access[J] .Ship Electronic Engineering,2007, 27(3):17-19.(in Chinese)

[ 3] 高尚,杨静宇, 吴小俊.求解指派问题的交叉粒子群优化算法[ J] .计算机工程与应用, 2004, 40(8):54-55.

GAO Shang,YANG Jing-yu,WU Xiao-jun.Using Particle Swarm Optimization Algorithm with Crossover to Solve Assignment Problem[ J] .Computer Engineering and Applications,2004,40(8):54-55.(in Chinese)

[ 4] 谈文芳,赵强,余胜阳,等.改进粒子群优化算法求解任务指派问题[J] .计算机应用,2007,27(12):2892-2895.

TAN Wen-fang, ZHAO Qiang, YU Sheng -yang, et al.Solving task assignment problem based on improved particle swarm optimization algorithm[ J] .Journal of Computer Applications, 2007, 27(12):2892-2895.(in Chinese)

[ 5] 陈自卫,石雄.基于遗传算子的粒子群算法在战场频率分配中的应用[J] .舰船电子工程,2010,30(3):73-76.

CHEN Zi-wei, SHI Xiong.Application of Particle Swarm Optimization Based on Genetic Operator in Frequency Assignment on Battlefield[ J] .Ship Electronic Engineering, 2010,30(3):73-76.(in Chinese)

[ 6] 于江,张磊.一种基于遗传算法的战场频率分配方法[ J] .电讯技术, 2011, 51(7):90-96.

YU Jiang, ZHANG Lei.A Battlefield Frequency Assignment Method Based on Genetic Algorithm[ J] .Telecommunication Engineering, 2011, 51(7):90-96.(in Chinese)

[7] Smith D H, Taplin R K,Hurley S.Frequency Assignment with Complex Co-Site Constraints[ J] .IEEE Transactions on Electromagnetic Compatibility,2001,43(2):210-218.

[8] Eberhartr R C, Kenndy J.A new optim izier using particle swarm theory[C]//Proceedings of the 6th International Symposium on Micro Machine and Human Science.New York:IEEE, 1995:39-43.

[9] Clerc M.Discrete particle swarm optimization[ M] .Berlin:Springer Verlag,2004:219-240.

[10] 孙晓雅,林焰.一种新的离散粒子群算法在指派问题中的应用[ J] .计算机应用研究,2009,26(11):4091-4094.

SUN Xiao-ya, LIN Yan.Using new DPSO algorithm to solve assignment problem[J] .Application Research of Computers,2009,26(11):4091-4094.(in Chinese)