一种基于经验模态分解的信噪比盲估计新算法✴

李国汉，王可人，张颂

一种基于经验模态分解的信噪比盲估计新算法✴

李国汉，王可人，张颂

（解放军电子工程学院信息系，合肥230037）

为了增强未知样式信号的信噪比估计性能，提出了一种基于经验模态分解（EMD）的信号信噪比估计新算法，通过固有模态函数（IMF）分量平均周期判断信号与噪声界限。给出了经验模态分解估计法的工作原理和流程图，分析了经验模态分解估计法的性能。仿真结果表明，与信号空间分解法一样，经验模态分解估计法能够实现盲信号信噪比估计，后者估计均方误差比前者要小，在0 dB信噪比下均方误差不超过0.3 dB。

信噪比估计；盲估计；经验模态分解；子空间分解

1 引言

信噪比是信号强度和背景噪声的比值，作为表征通道特性的参数，它是实现多项通信信号处理技术的重要依据，如功率控制、译码截止条件的设定、自适应调制编码等，获得精确的信噪比估计可以提高这类技术的性能。在非协作的通信环境中，信噪比估计值直接影响调制方式盲识别的效果，无论是基于统计模式识别还是基于最大似然的调制识别算法，都需要信噪比的估计值作为必需的先验知识，否则将很大程度上影响识别算法的性能［1］。因此，有关信噪比估计方法的研究一直受到广泛的关注，文献［1］对传统的信噪比估计法进行了总结。

Benedict和Soong较早应用二阶、四阶矩（M2M4）在加性高斯白噪声通道中分别对载波强度和噪声强度进行估计，文献［2］对其改进用于QPSK信号信噪比估计。Brand等提出了信号方差比（SVR）估计算法，该算法基于多阶矩方法，用于多径衰落信道的质量监控。Brando等给出了复信道中的自适应信号噪声方差比（SVR）估计，但该算法的缺点是只能应用于MPSK信号，对于其他调制方式则很难应用。除了上述确定信号信噪比估计算法外，还有一些适用范围广泛的盲估计算法。信号子空间（SB）分解算法是由Andersin针对窄带TDMA蜂窝通信系统提出来的，其后有系列文章对其完善和改进［3-5］。该估计法的优越性在于无需知道信道情况，通过信号协方差矩阵的特征值分解将信号与噪声从信号中分离出来，从而具有适应信道特性的能力。子空间分解法不依赖于具体信号形式，在盲信号处理领域对于估计信噪比具有独特的优越性。但该算法中，信号与噪声的边界不容易准确界定，影响估计的准确性。

经验模态分解（EMD）法可用于提取含噪信号的噪声分量和信号分量。本文将EMD法引入信噪比估计，以改善子空间分解法精度不高的局限性，也可不要信号样式的这一先验条件，适合盲信号处理领域。

2 信号子空间分解法

假设调制信号s（n）通过加性高斯白噪声信道，接收信号无失真采样后由下式表示：

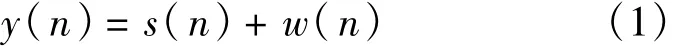
其中，w（n）是均值为零、方差为σ2w的高斯白噪声。信号和噪声分布独立，对接收信号进行分组，每组样点数M，组成向量y（k），可令y（k）=［y（1，k），y（2，k），…，y（M，k）］T。接收信号的自相关矩阵为

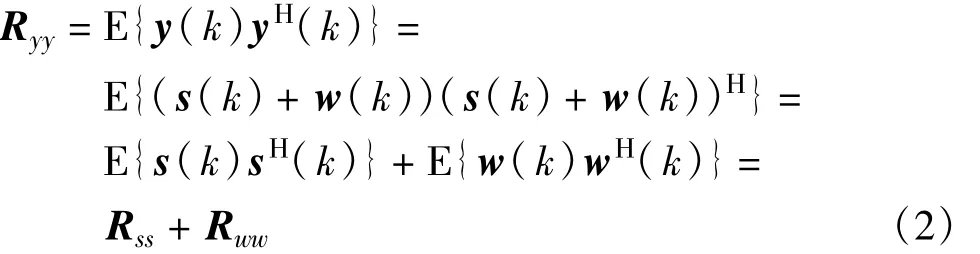
其中自相关矩阵阶数为M，由于上式中矩阵Ryy、Rss和Rww均为Hermitian阵，因此可以进行特征值分解（EVD）：

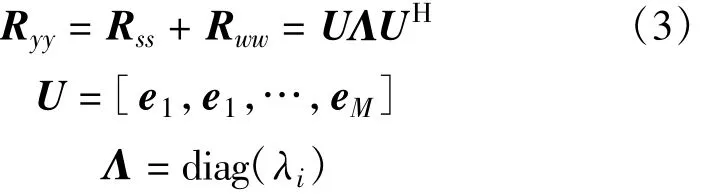
其中，λ1≥λ2≥…≥λM；e1，e1，…，eM为相应的特征向量；

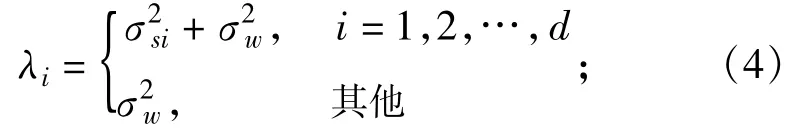
σ2si为第i个信号子空间分量的功率，可以选择最大的d个特征值来构造，这样我们可以计算信号功率，进而计算信噪比

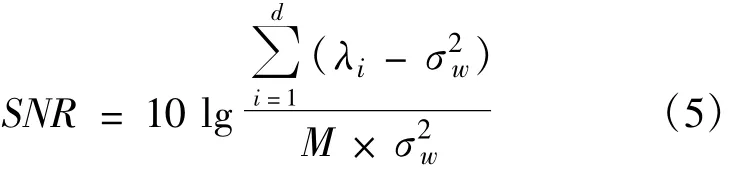
信号子空间维数d估计的精确与否直接关系到算法的估计效果。SB算法中直接应用MDL原理进行估计。在实际应用中，接收信号数字化前都要经过限带滤波和过采样，高斯白噪声一般都是比信号带宽稍宽的窄带高斯白噪声，因此含噪信号空间维数d1＜M（这里M为自相关矩阵阶数）。噪声的平均功率可由下式计算：

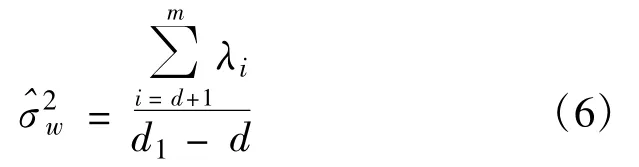
可以看到，信号维数d和噪声维数d1的准确估计对噪声估计至关重要。可以通过下面的步骤估计信号维数d和噪声维数d1。首先估计噪声维数，定义球面函数［5］

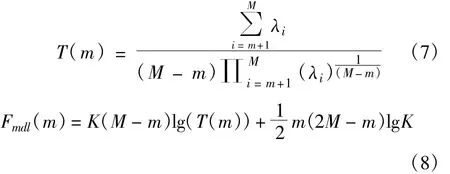
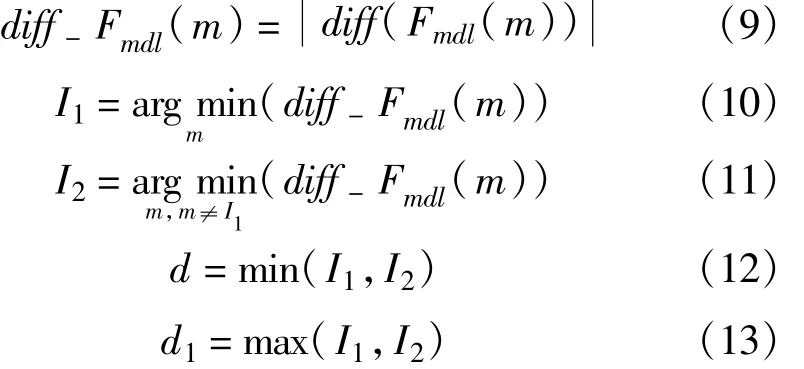
其中，diff（·）表示求序列差分函数。代入式（6）得到噪声功率估计，那么信号功率估计值为

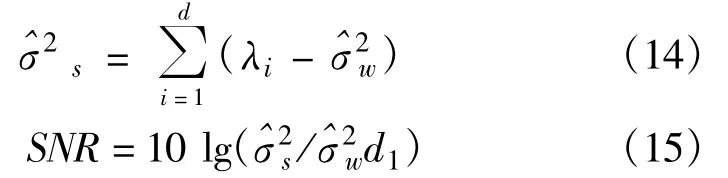
基于子空间分解的方法不需要知道信号的具体形式，这优于其他方法，但是由于其估计噪声功率时不易找出信号与噪声的分界点，而且随着空间维数的增大，最小的几个特征值（与分解残差相关）对噪声功率估计的影响很大［4］，这会进一步增加估计误差。

3 基于EMD分解的SNR估计

3.1EMD分解

1996年，供职于NASA的美籍华人Norden E. Huang等人在对瞬时频率的概念进行了深入研究后，提出了Hilbert-Huang变换方法。这一方法创造性地提出了固有模态函数（IMF）的概念以及将任意信号分解为固有模态函数的方法——经验模式分解。

对于固有模态函数，可以用Hilbert变换构造解析信号，然后求出瞬时频率。而对于一般不满足固有模态函数条件的复杂信号，先要采用EMD方法将其分解。任何时候，一个信号都可以包含许多固有模态函数，固有模态函数相互迭加，便形成复杂信号。在此假设的基础上，可以采用EMD方法，对任何信号x（t）进行分解具体步骤在许多文献里有介绍［8-10］，在此不详细列出。

3.2固有模态函数判据的选择

EMD的分解过程其实是一个“筛分”的过程，在“筛分”过程中，不仅消除了模态波形的迭加，而且“使波形轮廓更加对称”。EMD方法从特征时间尺度出发，首先把信号中特征时间尺度最小的模态分离出来，然后分离特征时间尺度较大的模态，最后分离特征时间尺度最大的分量。以下综合整个EMD“筛分”的详细步骤，给出了详细的计算流程图，如图1所示。

图1 EMD分解流程Fig.1 Flowchart of EMD

要分解出IMF分量，必须确定IMF的判据，因为EMD分解过程是一个“筛分”过程，在3次样条拟合的过程中可能产生人为干扰，一般情况下，需要多次迭代才能分解出一个IMF分量，“筛分”次数越多，包络线的平均值可能会越接近零，但是如果“筛分”次数太多，只能得到定常振幅的调频波，这就会失去原始信号的真实物理意义。一般地，采用由“筛分”前后结果h（t）得到的标准差，即式（16）的大小来控制迭代次数。

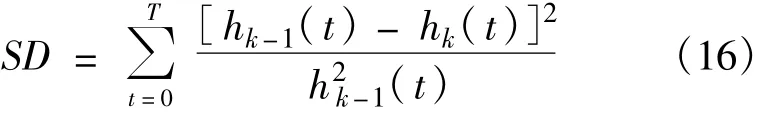
大量的计算结果表明合理地确定迭代阈值是非常重要的。实践表明，迭代阈值SD设为0.2～0.3比较合适［9］。

文献［11］通过详细研究白噪声序列经EMD滤波分解后各IMF分量的性质，指出EMD分解的多个IMF分量前面几个是以噪声为主的分量，逐渐过渡到信号能量占绝大部分的IMF分量，第k个IMF分量的周期大约是第k-1个分量周期的2倍。

3.3基于EMD法的信噪比估计

由前面的分析可以看出，假设一段信号x（t）分解得到N个IMF分量，前k个是以噪声能量为主的分量，那么信噪比为

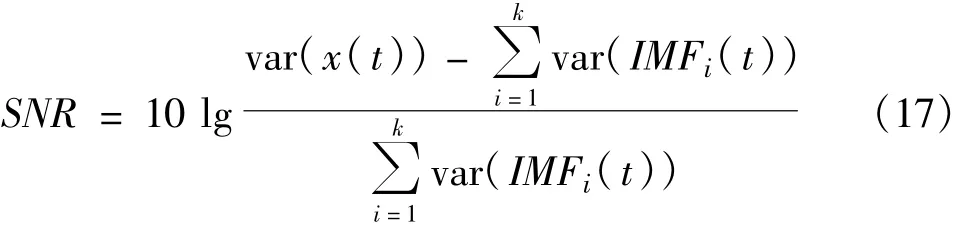
由这个表达式可以看出来，准确估计信噪比关键在于确定噪声IMF分量与信号IMF分量的分界点k，这可以通过白噪声EMD分解性质2来求得。先求第一个分量的平均周期，记为T1：

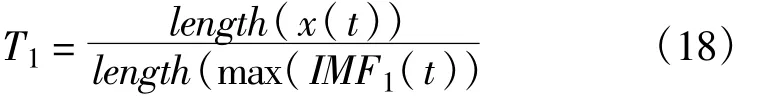
式中，分母项表示第一个IMF分量的极大值点个数，分子项为分析序列采样点数。以此类推得到T1，T2，…，TN。令

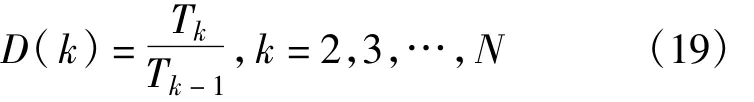
D（k）开始为2，直到突然偏离2为止，即达到噪声与信号的分界点。在这之前的几个分量方差和作为噪声功率，原信号功率减去噪声功率作为信号功率估计，进而求出信噪比，如式（17）所示。

4 仿真结果与分析

4.1信号与噪声分界点的仿真

运用Matlab进行计算机仿真，采用OFDM调制，取符号周期Tu=244μs，子载波数N=1 705，保护间隔采用循环前缀Tg=0.25Tu，载频fc=90 MHz，即DVB-T的一个工作模式，信道环境为AWGN，固定SNR=10 dB。

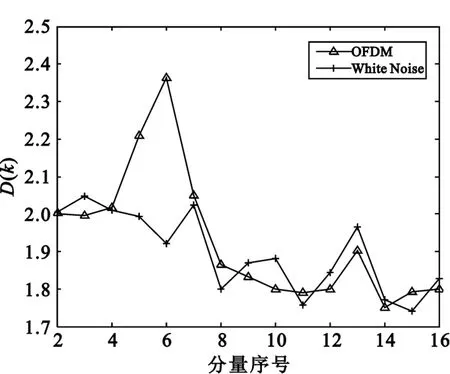
图2 含噪OFDM信号与白噪声平均周期比曲线Fig.2 The IMF average period rate of noise and OFDM signal

由图2可以看出，纯噪声信号的IMF分量正如理论推导所言，前后相邻分量的平均周期比为2，而含噪信号的前后分量平均周期在第6个分量处变化明显，不再服从平均周期2倍递增的关系，即在此处IMF分量的频率有较大的跌落，此处可以当作噪声与信号分量的分界点。

4.2EMD估计SNR的性能仿真

仿真条件不变，设定实际信噪比0～25 dB，通过式（25）、（26）提取噪声分量，然后估计信噪比。图3显示了用EMD法估计的性能，可以看出EMD法能实现信噪比有效估计，估计误差不超过1 dB。同时，由估计具体过程可以看出，该估计法不依赖于具体信号样式，由于使用OFDM信号进行仿真，还可看出该方法对非恒模信号有效。

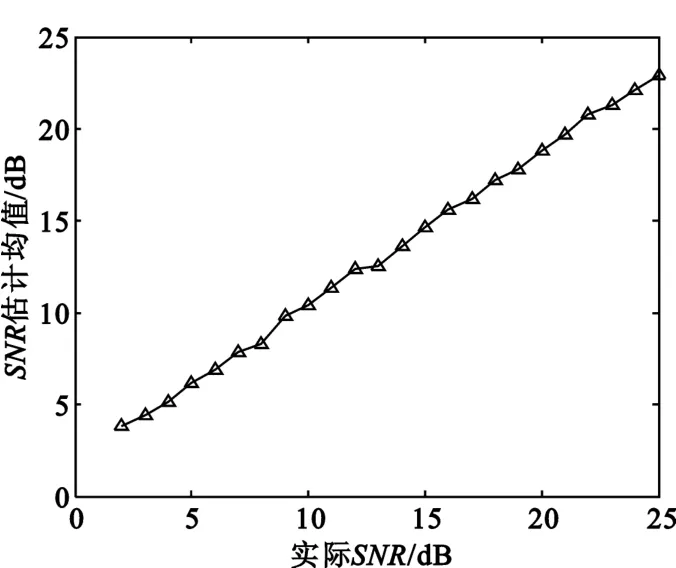
图3EMD法SNR估计曲线Fig.3 The curve of EMD-based SNR estimation algorithm

图4 对比了EMD法和信号空间分解法的性能。间隔1 dB，每1 dB进行50次仿真，统计各自的均方误差。信号空间分解法按照第2节的步骤进行。仿真结果表明，两者性能均随SNR的增加而改善，但EMD法比信号空间分解法性能更优，特别是在低性噪比条件更为明显。从图4可以看出在信噪比为0 dB附近，随着SNR降低子空间方法误差迅速扩大，而EMD方法误差不超过0.3 dB。

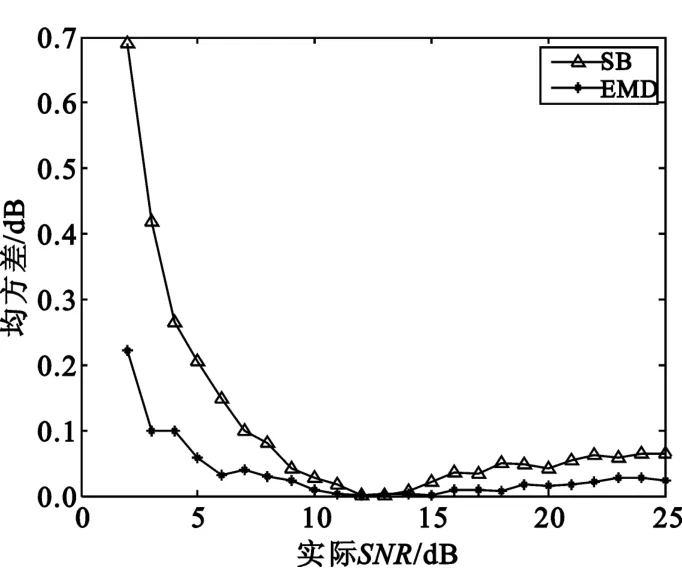
图4 估计均方差曲线（50次）Fig.3 The curves of estimated mean square error（50 trials）

5 结束语

SNR作为信号质量的重要指针，向来得到通信领域研究的重视，随着自适应通信、认知无线电等领域的迅速发展，盲信号质量估计具有越来越重要的意义。本文将EMD分解法引入信号SNR估计，提出了一种新的SNR估计法，理论分析和仿真表明，该方法与空间分解法一样具有较强的信号样式适应性，同时在相同条件下比子空间分解法的精度更高，适合用于信号监测、认知无线电等领域。

［1］Pauluzzi D R，Beaulieu N C.A comparison of SNR estimation techniques for the AWGN channels［J］.IEEE Transactions on Communications，2000，48（10）：1681-1691.

［2］Ren Guang-liang，Chang Yi-lin，Zhang Hui.A new SNR′s estimator for QPSK modulation in an AWGN channel［J］. IEEE Transactions on Circuits and Systems II，2005，52（1）：336-338.

［3］范海波，陈军，曹志刚.AWGN信道中非包络信号的SNR估计方法［J］.电子学报，2002，30（9）：1369-1371.

FAN Hai-bo，CHEN Jun，CAO Zhi-gang.An algorithm of SNR esitmation for non-constant envelop signal in the AWGN channel［J］.Acta Electronica Sinica，2002，30（9）：1369-1371.（in Chinese）

［4］詹亚锋，曹志刚，马正新.无线数字通信的盲信噪比估计［J］.清华大学学报（自然科学版），2003，43（7）：957-960.

ZHAN Ya-feng，CAO Zhi-gang，MA Zheng-xin.Blind SNR estimates in wireless digital communications［J］.Journal of Tsinghua University（Science and Technology），2003，43（7）：957-960.（in Chinese）

［5］Andersin M，Mandayam N B，Yates R D.Subspace based estimation of the signal to interference ratio for TDMA system［C］／／Proceedings of IEEE 46th Vehicular Technology Conference.Atlanta，Georgia，USA：IEEE，1996：1155-1159.

［6］顾学迈，吴丹.一种基于联合信息标准的盲信噪比估计算法［J］.南京航空航天大学学报，2007，39（3）：363-367.

GU Xue-mai，WU Dan.Signal to noise ratio algorithm based on CIC［J］.Journal of Nanjing University of Aeronautics＆Astronautics，2007，39（3）：363-367.（in Chinese）

［7］隋丹，葛临东.一种新的基于改进PASTd的中频信号盲信噪比估计算法［J］.电子与信息学报，2007，29（7）：1657-1661.

SUI Dan，GE Lin-dong.A novel blind SNR estimator based on the modified PASTd algorithm for IF signals［J］.Journal of Electronics＆Information Technology，2007，29（7）：1657 -1661.（in Chinese）

［8］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society A，1998，454（1971）：903-995.

［9］于德介，程军圣，杨宇.机械故障诊断的Hilbert-Huang变换方法［M］.北京：科学出版社，2006.

YU De-jie，CHENG Jun-shen，YANG Yu.Hilbert-Huang transformation in Machine Exception Diagnose［M］. Beijing：Science Press，2006.（in Chinese）

［10］相小谊.基于Hilbert-Huang变换的信号分析及应用［D］.西安：西安电子科技大学，2008：19-22.

XIANG Xiao-yi.The analysis and application of signal based on Hilbert-Huang Transform［D］.Xi′an：Xidian U-niversity，2008：19-22.（in Chinese）

［11］Flandrin P，Rilling G，Goncalves P.Empirical mode decomposition as a filter hank［J］.IEEE Signal Processing Letters，2003，11（2）：112-114.

LI Guo-han was born in Longyan，Fujian Province，in 1984. He received the M.S.degree in 2009.He is currently working toward the Ph.D.degree.His research interests include communication signal processing and non-cooperative communication.

Email：liguohan521＠163.com

王可人（1957—），男，江苏镇江人，1986于解放军理工大学通信工程学院获硕士学位，现为教授、博士生导师，主要研究方向为无线通信、信号处理等；

WANG Ke-ren was born in Zhenjiang，Jiangsu Province，in 1957.He received the M.S.degree from PLA University of Science＆Technology in 1986.He is now a professor and also a Ph.D.supervisor.His research interests include wireless communication and signal processing.

张颂（1984—），男，江苏徐州人，2011年获博士学位，现为工程师，主要研究方向为无线通信、信号处理等。

ZHANG Song was born in Xuzhou，Jiangsu Province，in 1984.He received the Ph.D.degree in 2011.He is now an engineer.His research interests include wireless communication and signal processing.

A Novel Blind SNR Estimation Algorithm Based on Empirical Mode Decomposition

LI Guo-han，WANG Ke-ren，ZHANG Song
（Information Department，Electronic Engineering Institute，Hefei 230037，China）

To enhance the performance Signal-to-Noise ratio（SNR）estimation of unknown type signals，a novel algorithm based on Empirical Mode Decomposition（EMD）is proposed，in which the boundary of the signal and noise is determined by the average period of Intrinsic Mode Functions（IMF）.The principle and flow chart of the algorithm are presented，and the EMD-based method performance is also analysed.Simulation results show that，like the method based on signal subspace decomposition，EMD-based method can adapt to unknown signals SNR estimation，the estimated Mean Square Error（MSE）of EMD-based method is smaller than the former，and it is not more than 0.3 dB when the SNR is 0 dB.

SNR estimation；blind estimation；empirical mode decomposition（EMD）；subspace decomposition

The Doctor Innovation Foundation of PLA Electronic Engineering Institute

TN911.4

A

10.3969／j.issn.1001-893x.2012.05.012

李国汉（1984—），男，福建龙岩人，2009年获硕士学位，现为博士研究生，主要研究方向为通信信号处理、非协作通信；

1001-893X（2012）05-0663-05

2012-01-20；

2012-03-13

解放军电子工程学院博士创新基金资助项目