梯度复合板界面对Ⅲ型内部周期裂纹影响

万景燕，霍华颂，时朋朋

(1.长安大学理学院，陕西西安710061;2.宁夏大学数学计算机学院，宁夏银川750021)

工程中常将不同梯度材料拼接使用，以满足对材料性能的多重要求。为能够充分发挥功能梯度材料中各组成材料的特性，满足工程实际需求，须在材料设计上寻求最佳分布梯度，以期最大限度地缓和由机械或热机械行为失配所引起的应力不均。因此，研究功能梯度材料断裂行为成了其设计中的重要问题。

许多学者都对功能梯度材料的断裂力学做了研究，Erdogan在功能梯度材料断裂力学理论研究方面做了卓有成效的工作，他和他的合作者解决了在不同机械载荷和热载荷作用下功能梯度材料断裂的一些基本问题［1-5］。文献［6］研究了压电材料中垂直于界面的周期裂纹问题，文献［7］求解了含周期裂纹的接触问题。目前国内外对周期裂纹问题讨论较少，文献［8-9］运用积分变换和奇异积分方程方法求解了反平面载荷下功能梯度材料中单周期分布裂纹的应力强度因子，文献［10］借助Fouirer级数和传递矩阵方法得到周期问题的Hilbert核奇异积分方程，考虑的是由功能梯度涂层和无限弹性基体构成的材料模型，文献［11］通过叠加原理用含无穷项积分形式的奇异积分方程求解梯度材料的周期界面问题，研究的是单个功能梯度带材料。本文求解两个功能梯度条带弱间断粘结的复合结构，其中一个板条内部存在周期裂纹。通过运用有限傅里叶变化简洁的将混合边值问题的求解转化为Hilbert核奇异积分方程，并运用 Lobatto-Chebyshev方法对问题进行数值求解。

1 问题描述

图1，厚度为h1与h2的两个无限长功能梯度板条弱间断粘结成复合板条，采用直角坐标系(x，y)，材料的粘结界面位于x轴上，距粘结界面h的位置存在周期裂纹，最小周期带宽为2L，每个周期带内存在单个裂纹，长度为2a。y轴穿过裂纹中心且垂直于裂纹面。m0为材料1和材料2的粘结界面处的剪切模量。结构的剪切模量使用双参数的指数模型(材料1、2中的各种参数均用上标1、2标出)。

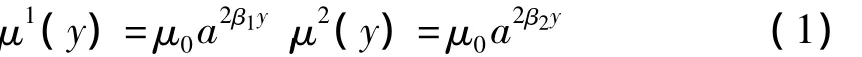
式中μ0-粘结界面上的剪切模量和密度;α，β1，β2-描述材料非均匀性的参数。

在反平面变形情况下，功能梯度层的本构平衡方程、控制方程分别为(k=x，y;j=1，2)。

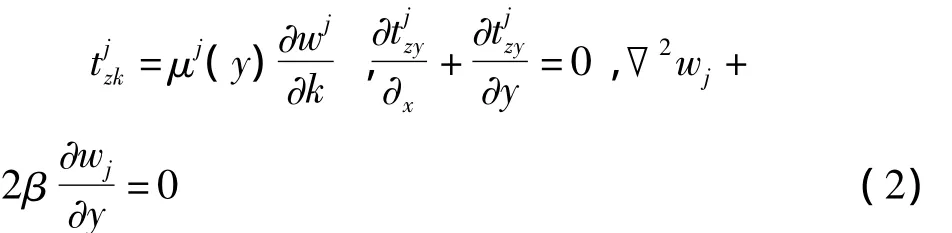
2 断裂分析

考虑周期性，问题的边界条件为

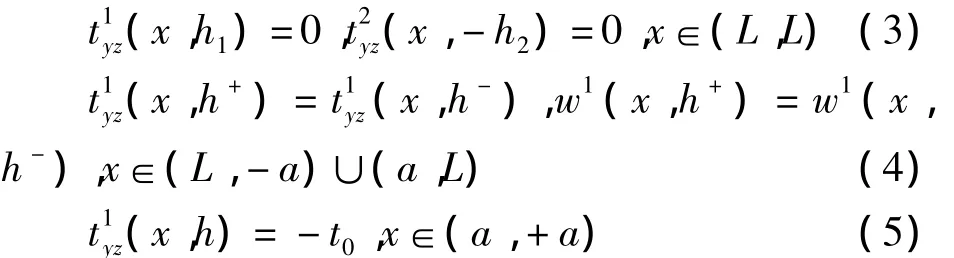
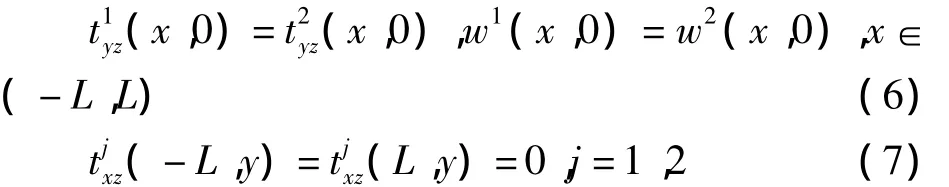
考虑问题周期性，利用有限傅里叶变换，得到反平面载荷下的位移解

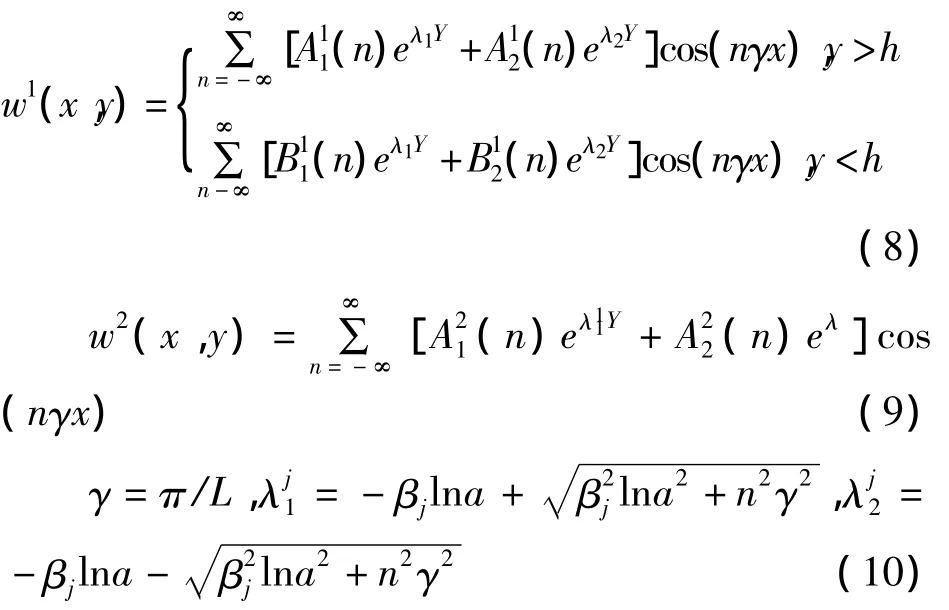
定义如下的位错密度函数

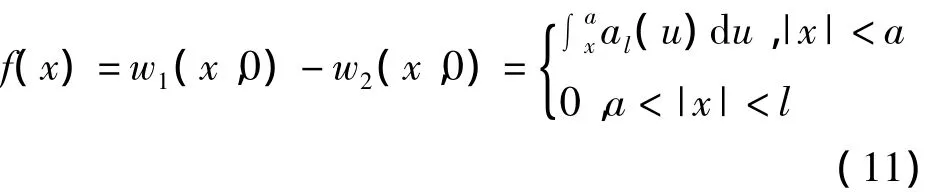
它满足如下条件

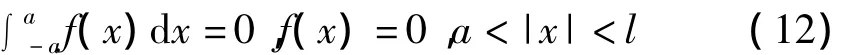
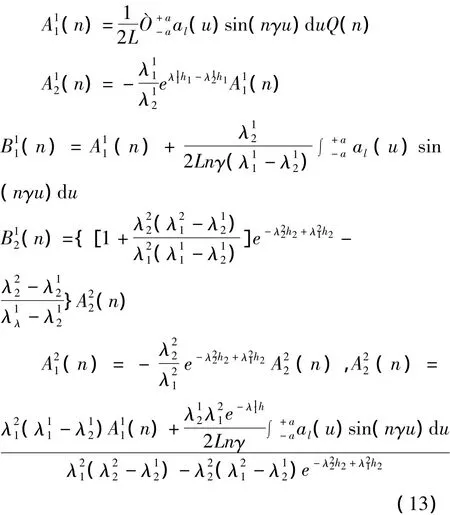
由边界条件式(5)可得到如下奇异积分方程

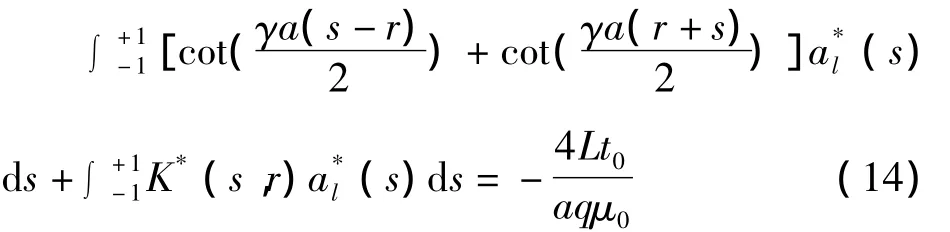
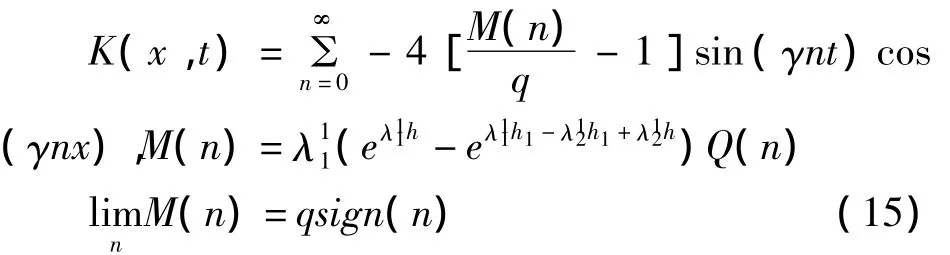
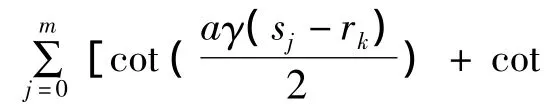
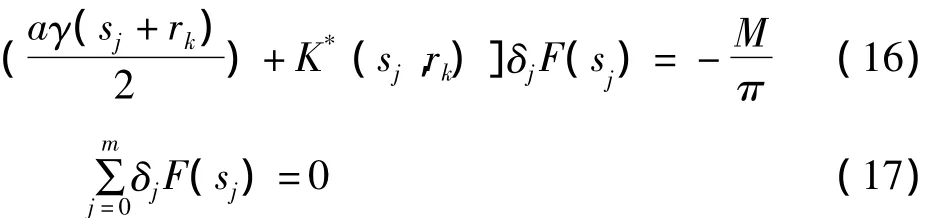
其中m为求积节点数，δ0=δm=1/2，δ1=…=δm-1=1。

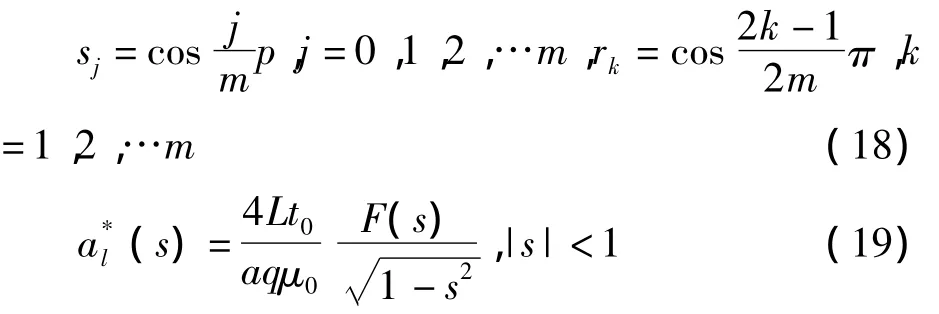
基于式(16)和式(17)式的数值解，可以进一步求得裂纹尖端标准化的应力强度因子表达式为

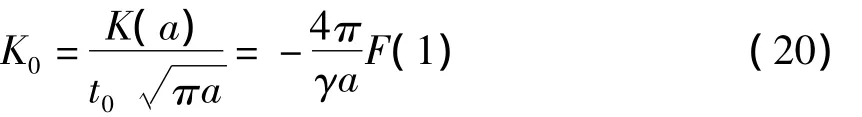
3 数值结果与讨论

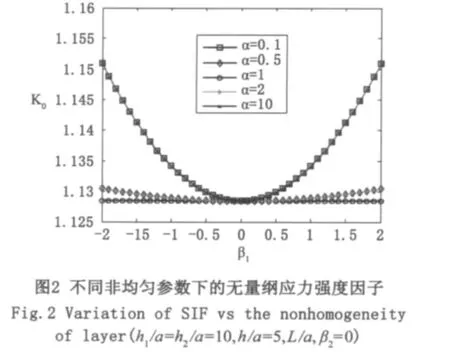
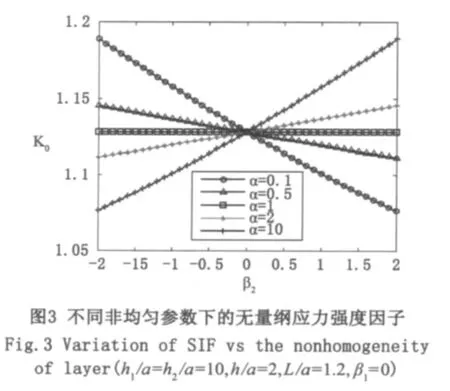
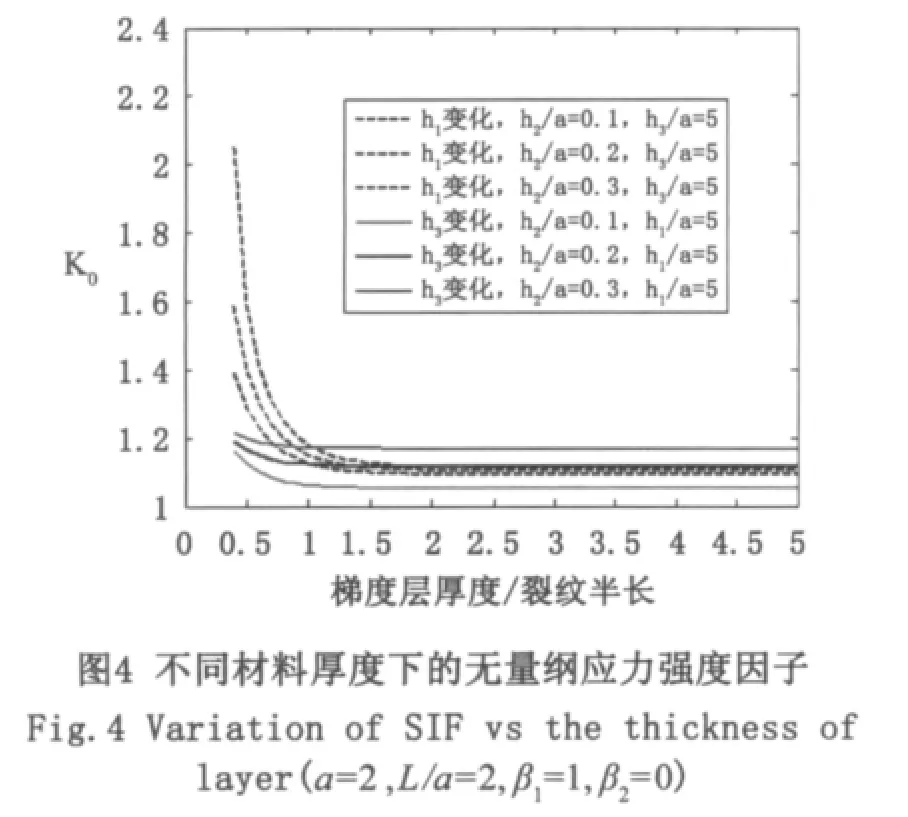
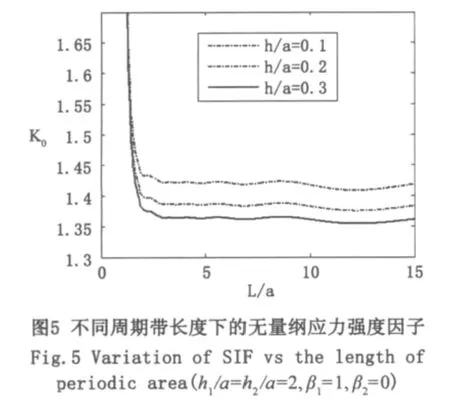
算例中材料粘结界面的物理参数选择为 m0=12×1010N/m2，进一步分析不同梯度材料的非均匀参数a，b1，b2，材料厚度h1，h2，裂纹与界面距离h以及最小周期带宽2L等对应力强度因子的影响，结果如图2-图5。图2、图3给出了不同梯度材料的非均匀参数(通过a，b1，b2体现)对裂尖应力强度因子的影响。从图2和图3可看出:非均匀参数a的不同导致指数型非均匀参数b1，b2的变化对界面裂纹的应力强度因子的影响不同。当a=1，应力强度因子达到最小，b1的变动对应力强度因子没有影响。当a1=1时，应力强度因子随着b1的增加而达到最小值，然后随着b1的增加而迅速变大。当lna距0越远，变化越大。从图2可以看出当a＞1时，应力强度因子随b2增大而变小。当a＜1时，应力强度因子随着b2增大而增大。当a=1时，显然各个功能梯度层均退化为非均匀层，指数型非均匀参数b1，b2的变动对应力强度因子没有影响。图4给出了不同的材料厚度(通过h1/a，h2/a体现)与界面距离(通过h/a体现)对裂尖应力强度因子的影响。从图4中可看出:裂纹尖端应力强度因子随着材料厚度的增加而减小。而且裂纹距界面越近，应力强度因子越大。图5反映的是不同的以及最小周期带宽(通过L/a体现)对裂尖应力强度因子的影响。从图5中可看出:裂纹尖端应力强度因子随着周期带宽的增加而迅速减小，最后达到稳定的数值。这是因为固定裂纹尺寸a，周期带尺寸L增大将使裂纹间距更加稀疏，从而有效地减弱裂纹间的相互影响，当L/a＞2.5时，裂纹周期分布导致的应力强度和单个裂纹情况下的结果差别很小，裂纹之间的干涉作用微弱，对裂纹端应力强度因子的影响可以忽略。

4 结论

1)随着材料厚度的增加，裂纹尖端的应力强度因子减小，内部裂纹距离弱间断界面越远，应力强度因子越小。

2)用双指数模型描述材料非均匀性时，不同的底数取值导致指数变量对应力强度因子的影响不同，选择适当的材料组合可以阻滞裂纹扩展。

3)随周期带宽的增加，可以有效地降低裂纹间的相互影响，降低裂纹尖端应力强度因子。

［1］DELALE F，ERDOGAN F.The crack problem for a nonhomogeneous plane［J］.Journal of Applied Mechanics，1983，50:609-614.

［2］DELALE F，ERDOGAN F.Interface crack in a nonhomogeneous elastic medium［J］.International journal of Engineering Science，1988，26(6):559-568.

［3］KONDA N，ERDOGAN F.The mixed-mode crack problem in nonhomogeneous elastic plane［J］.Engineering Fracture Mechanics，1994，47:533-545.

［4］ERDOGAN F.Fracture mechanics of functionally graded materials［J］.Composites Engineering，1995，5(7): 753-770.

［5］ERDOGAN F，B H WU.The surfaces crack problem for a plate with functionally graded properties［J］.Journal of Applied Mechanics，1997，64(3):449-456.

［6］X LI，S H DING.Periodically distributed parallel cracks in a functionally graded piezoelectric(FGP)strip bonded to a FGP substrate under static electromechanical load［J］.Computational Materials Science，2011(50):1477 -1484.

［7］Y T ZHOU，X LI.Coupled crack/contact analysis for composite material containing periodic cracks under periodic rigid punches action［J］.Tech Science CMES，2010，63(2):163-189.

［8］J CHEN.Anti-plane problem of periodic cracks in a functionally graded coating-substrate structure［J］.Arch Appl Mech，2006(75):138-152.

［9］S H DING，X LI.Anti-plane problem of periodic interface cracks in a functionally graded coating-substrate structure［J］.International Journal of Fracture，2008 (153):53-62.

［10］黄干云，汪越胜，余寿文.功能梯度涂层中的Ⅲ型周期裂纹问题［J］.机械强度，2004，26(S):097-099.

［11］陈宜周.弹性功能梯度材料板条中周期裂纹的反平面问题［J］.力学学报，2004，36(4):501-506.