并行算法性能简析

2012-03-17何怡芝

电子设计工程 2012年11期

何怡芝

（1．西北大学陕西西安 710069；2．陕西职业技术学院陕西西安 710100）

近年来，在市场需求的推动下，并行计算已经大量的应用于各个领域，如核武器、石油勘探、数值天气预报、地震数据处理、飞行器数值模拟和大型事务处理等，都需要每秒执行万亿次甚至百万亿次运算的计算机，然而基于这些应用问题本身存在的并行性和单机性能的限制，并行计算就成为满足计算机计算速度的惟一可行途径[2]。所谓并行计算[1]，就是将一个任务分解成多个子任务，同时分配给几个不同的处理器，各个处理器之间相互协同，并行地执行子任务，从而能够加速求解问题的速度，或者扩大求解应用问题的规模。

1 求PI值的MPI并行计算程序

#include “mpi．h”/* 是预处理指令，用于包含 mpi的头文件。

#include ＜stdio．h＞

double f（ double a ）{return （4．0/ （1．0+a*a））；} /*定义被积函数 f（x）。

intmain（int argc，char*argv[]） /*argc和 argv分别是命令行参数的个数和参数数组的指针。

{

intn，myid，numprocs，i，namelen；/*n ：计算区间分区数；myid：本进程的进程号；numprocs：进程组中进程数；i：进程中计算各个小区间的循环控制变量；namelen：处理器名长度。

double PI25DT=3．141592653589793238462643；/* 定义一个比较精确的25位π值作为标准值，以分析本程序计算结果的误差。

doublemypi， pi， h， sum， x； /*mypi：进程中所有小区间面积的求和值；pi：最终的计算π值；h：小区间宽度；sum：进程中所有小区间高的和；x：每个小区间中点的x值。

double startwtime，endwtime； /*定义变量开始时间startwtime和结束时间endwtime。均为MPI_Wtime（）的返回值。

char processor_name[MPI_MAX_PROCESSOR_NAME]； /*processor_name：处理器名存储单元。

MPI_Init（＆argc，＆argv）； /*argc 和 argv 分别是命令行参数的个数和参数数组的指针。

MPI_Comm_size（MPI_COMM_WORLD，＆numprocs）； /*用numprocs返回通信域MPI_COMM_WORLD中的进程数。

MPI_Comm_rank（MPI_COMM_WORLD，＆myid）； /* 用myid返回通信域MPI_COMM_WORLD中本进程的进程号。

MPI_Get_processor_name（processor_name，＆namelen）； /*该函数返回运行本进程的处理器名称。

fprintf（stderr，“Process%on%s ”，myid， processor_name）；

if（myid==0） {

n=10000；

startwtime=MPI_Wtime（）；

}/*是仅进程0执行的代码，给n赋值10 000意味着将0-1的积分区间分成10 000小块，对每一个小块计算面积。同时，获取计算机开始的时间。

MPI_Bcast（＆n， 1， MPI_INT， 0， MPI_COMM_WORLD）；/*表示通信器MPI_COMM_WORLD中进程号为0的进程将自己n中的内容发送给通信器中所有其他进程。

If（n==0）

done=1；

else{

h=1．0/（double） n；

sum=0．0；

for（i=myid； i＜ n； i+=numprocs） {

x=h* （（double）i+0．5）；

sum+=f（x）；

}/*计算本进程所分配的各小块的高度和。每一进程均从i=myid开始，每做一次计算往后跳numprocs块。

mypi=h*sum；/*mypi=h*sum将每个进程所得的各小块的高度和与小块宽度相乘即得本进程所得的小块面积和即PI的部分值。

MPI_Reduce（＆mypi，＆pi， 1， MPI_DOUBLE， MPI_SUM，0，MPI_COMM_WORLD）；/*将各进程所得的PI的部分值进行归约。

if（myid==0） {

printf （“pi is approximately%．16f， error is%．16f ”， pi，pi-PI25DT）；

endwtime=MPI_Wtime（）；

printf（“wall clock time=%f ”， endwtime-startwtime）；

}}/*0号进程执行的代码，进程首先获取时间，再用现在的时候减去初始获取的时间即得到程序执行的时间并显示。

MPI_Finalize（）；/*让系统释放分配给MPI的资源。

return 0；

}

所有的进程都是从前到后依次执行该程序。

2 并行计算的加速比和效率分析

加速比和效率[1]是衡量一个并行程序性能的最基本的评价参数。其计算的方式如下：在处理器资源独享的前提下，假设某个串行应用程序在某台并行机单处理器上的执行时间为Ts，而该程序并行化后，P个进程在P个处理器并行执行所需要的时间为Tp，该并行程序在该并行机上的加速比Sp可定义为：效率定义为

2.1 并行算法中的几种假设

2.1.1 假设一

计算规模n=20 000，节点变化

1）节点为 1时

Process 0 on node9

pi is approximately 3．1415926537981260， Error is 0．0000000002083329

wall clock time=0．001900

2）节点为 2时

当测试两个结点时：

Process 0 on node9

Process 1 on node8

pi is approximately 3．1415926537981315， Error is 0．0000000002083368

wall clock time=0．001545

3）节点为 3时

Process 0 on node9

Process 1 on node8

Process 2 on node6

pi is approximately 3．1415926537981351， Error is 0．0000000002083415

wall clock time=0．001238

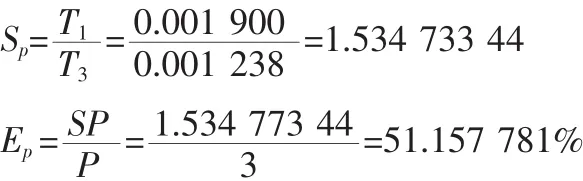
2.1.2 假设二

结点个数固定为3，计算规模n不断变化

1）当 n=30 000时

Process 0 on node9

Process 1 on node8

Process 2 on node6

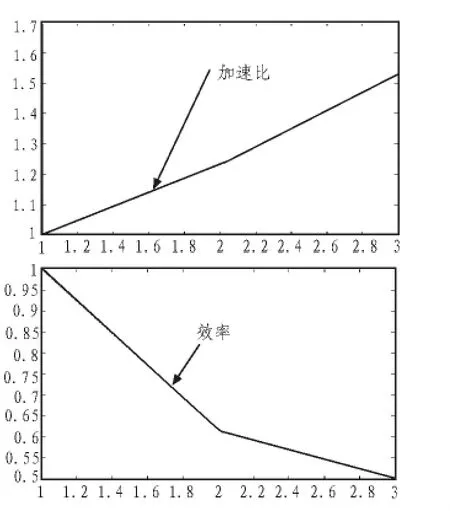
图1 计算规模n=20 000，节点变化时，加速比和效率的值Fig．1 Scale of calculate n=20 000， the node changes，speedup and efficiency

pi is approximately 3．1415926628490523， Error is 0．0000000092592591

wall clock time=0．000913

2）当 n=55 000 时

Process 0 on node9

Process 1 on node8

Process 2 on node6

pi is approximately 3．1415926536173409， Error is 0．0000000000275477

wall clock time=0．002289

3）当 n=222 000时

Process 0 on node9

Process 1 on node8

Process 2 on node6

pi is approximately 3．1415926535914891， Error is 0．0000000000016960

wall clock time=0．006891

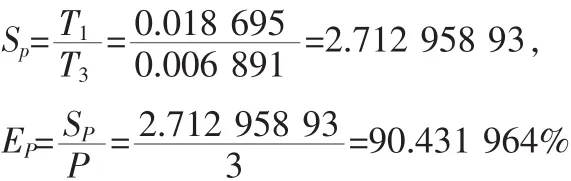
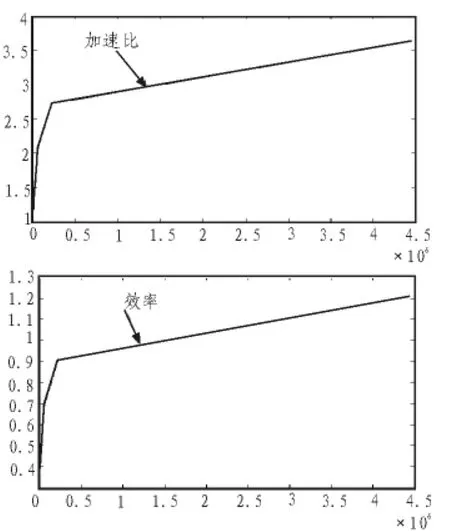
图2 结点个数固定为3，计算规模n不断变化时，加速比和效率的值Fig．2 Number of nodes is 3， n changing， speedup and efficiency

2.2 加速比和效率分析结果

由以上的加速比和效率图可知，问题规模较小n等于20 000时，进程执行的墙上时间和加速比随着节点数的增加而增大，效率随着节点数的增加而减少，原因是进程启动、调用、切换等时间开销所占的比例相对较大；而问题规模较大时，加速比和效率均随着规模的增加而增加，进程启动、调用、切换等时间开销所占的比例相对较小，说明该程序适合进行并行计算，并行的优势体现的更明显。