基于MATLAB与FPGA的FIR滤波器设计与仿真
2012-03-17刘春雅
刘春雅
(陕西国防工业职业技术学院 机电工程系,陕西 西安 710300)
数字滤波技术广泛应用于科学技术的各个领域,如通信、雷达、数字电视、生物医学等等,已成为极其重要的一门学科和技术领域。数字滤波器是对数字信号进行滤波处理以得到期望的响应特性的离散时间系统。数字滤波器工作在数字域,它处理的对象是经由采样器件将模拟信号转换而得到的数字信号。它的设计方法有很多,比较常用的有窗函数法、频率抽样法和最佳一直逼近法,但这些设计方法在设计滤波器尤其是高阶滤波器时工作量很大,而利用MATLAB信号处理工具箱进行数字滤波器的设计工作,能够减少工作量,提高设计效率。文中使用MATLAB这一高效工具完成一种FIR滤波器的前期参数设计工作,随后给出了FPGA实现该FIR滤波器的设计方案,最后通过MATLAB和ModelSim的联合仿真,验证了该FIR滤波器满足设计要求。
1 FIR滤波器数学模型
FIR滤波器为有限长脉冲响应滤波器,它的单位脉冲响应h(n)只有有限个数据点。输入信号经过线性时不变系系统输出的过程是一个输入信号与单位脉冲响应进行线性卷积的过程,可以用线性常系数差分方程表示如下:

式中,x(n)是输入信号,y(n)是卷积输出,b(n)是系统的单位脉冲响应。可以看出,每次计算y(n)需要进行N次乘法和N-1次加法操作,实现乘累加之和,其中N是滤波器单位脉冲响应b(n)的长度。
根据差分方程表达式可知,FIR滤波器输出是由移位、乘法和加法3种运算组成的。FPGA内部有大量触发器及相应的RAM和DSP资源,移位操作可以由触发器构成的移位寄存器链或RAM实现,而乘法和加法操作可以由DSP单元完成。故FPGA器件非常适合进行数字滤波器的设计实现。
2 具有线性相位特性的FIR滤波器
离散时间系统的相频响应反应了输入信号的各频率成分通过系统后在时间上发生位移的情况,一个理想的离散时间系统,除了具有所希望的幅频响应外,最好还能具有线性相位,尤其在在语音合成、波形传输等通信领域体现的较为明显。
设一个离散时间系统的幅频特性等于1,而相频特性具有如下的线性相位:

式中,k为常数,上式表明,该系统的相移和频率成正比。那么,当信号x(n)通过该系统后,其输出y(n)的频率特性:

故 y(n)=x(n-k),输出 y(n)等于输入在时间上的位移,达到了无失真输出的目的。
可以证明,当 FIR 系统的单位抽样响应满足 h(n)=±h(M-n)时,该系统具有线性相位。也就是说,FIR的单位抽样响应需满足对称条件时,滤波器具有线性相位特性。其中,M可以是偶数或奇数,它们对应的滤波器的结构形式有所不同,但是实现方式上没有太大的区别。
3 FIR滤波器的结构形式
FIR滤波器的实现结构通常有:直接型,转置型和线性相位型3种结构。由第一节的线性常系数差分方程式可以很容易地得到直接型的滤波器结构,如图1所示。
转置型由直接型可以推导得出,所实现的结构较直接型能够省一些FPGA的寄存器资源。但不论是直接型还是转置型,都不能够节省DSP单元的数量。而对FPGA来说,DSP资源占用情况是考量滤波器设计是否合理的重要参考依据,因为FPGA中的DSP单元是一种比较宝贵的硬核资源。故在较大规模的设计中,直接型和转置型两种滤波器结构使用很少,所以这里并不做论述。
线性相位型的结构分为滤波器阶数为偶数和奇数两种情况,当滤波器阶数N为奇数时,FIR的滤波器结构如图2所示。

图1 直接型的FIR滤波器结构Fig.1 Direct form FIR structure

图2 线性相位型FIR滤波器结构(N为奇数)Fig.2 Linear-phase form FIR structure
从图2可以看出,这种滤波器结构能够节省50%的乘法运算,这样FPGA的滤波器设计可以节约一半的DSP单元,是有利于FPGA实现的一种结构。
4 滤波器系数设计
FDATool(Filter Design&Analysis Too1)是 Matlab 信号处理工具箱专用的滤波器设计分析工具,操作简单、灵活,可以采用多种方法设计FIR滤波器。这种方法设计的数字滤波器,可以随时调整滤波器特性,而且滤波结果实时显示在图形区,减少了工作量,有利于滤波器设计的进一步优化。
根据给定的滤波器设计指标,FIR滤波器通带带宽为100 Hz,截止频率为200 Hz,主要完成滤除200 Hz以上干扰信号的工作,滤波器阶数为40阶。在FDATool中选用FIR低通滤波器设计,其幅频响应和相频响应如图3和图4所示。
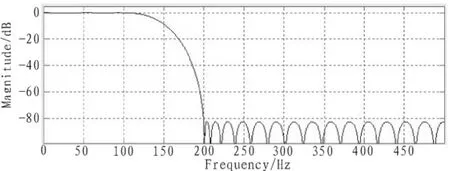
图3 幅频响应Fig.3 Magnitude response

图4 相频响应Fig.4 Amplitude response
从幅频响应和相频响应可以看出实现低通滤波功能的同时得到了一个具有线性相位特性的滤波器系数。
由于MATLAB计算得到的滤波器系数为浮点数,而FPGA只能处理定点数据,所以还需要通过MATLAB将浮点数通过量化取整后转化为定点数[7]。
5 FPGA实现及仿真结果
FPGA采用Xilinx公司的Spartan3A的XA3S200A器件,经过ISE软件综合后的滤波器顶层图如图5所示。
模块的资源占用情况如表1所示。
在MATLAB中产生一组测试数据来验证FPGA最终实现的功能和性能。测试数据源包含了有用信号和干扰信号。测试数据源的时域波形如图6所示。
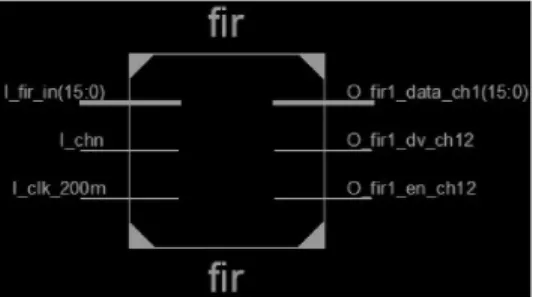
图5 滤波器顶层图Fig.5 Top view of FIR

表1 FIR模块资源占用情况Tab.1 Logic utilization of FIR module

图6 测试数据波形Fig.6 Test datawaveform
信号从时域上无法区分干扰信号的具体频率位置,通过对测试数据源做FFT变换,得到频域图如图7所示。

图7 测试数据源频谱图Fig.7 Test data in frequence domain
从频谱上大致可以看出这组测试源有用信号频点在50 Hz,另外3个干扰信号频点在250 Hz,300 Hz和400 Hz的位置上。通过FPGA实现的FIR滤波器进行滤除干扰信号后的信号的频谱如图8所示。
滤波后信号的时域图如图9所示。
从图8和图9可见,无论在时域还是频域均有效滤除了200 Hz以上的干扰信号,只保留了50 Hz的有用信号的频率成分。

图8 滤波后信号频谱图Fig.8 After filtered data in frequence domain

图9 滤波后信号的时域图Fig.9 After filtered datawaveform
6 结束语
研究了在FPGA中实现线性相位FIR滤波器的理论原理及设计方法,并在Xilinx FPGA器件上实现,借助ModelSim及MATLAB软件分别对FPGA实现结果和理论算法结果进行了仿真验证,经过数据分析,测试结果证明该FIR滤波器完全能够满足设计要求。
[1]徐志军,徐光辉.CPLD/FPGA的开发与应用[M].北京:电子工业出版社,2002.
[2]王冠,愈一鸣.面向CPLD/FPGA的Verilog设计[M].北京:机械工业出版社,2008.
[3]夏宇闻,胡燕翔.Verilog HDL数字设计与综合[M].北京:电子工业出版社,2009.
[4]胡广书.数字信号处理[M].北京:清华大学出版社,2003.
[5]刘树堂.数字信号处理(MATLAB版)[M].西安:西安交通大学,2008.
[6]田耕,徐文波.Xilinx FPGA开发实用教程[M].北京:清华大学出版社,2008.
[7]周云波,刘小群.基于Matlab的FIR数字滤波器的优化设计[J].电子科技,2010(10):28-29.
ZHOU Yun-bo,LIU Xiao-qun.Design of a digital filter FIR based on Matlab[J].Electronic Science and Technology,2010(10):28-29.
