基于可变风险SVM模型的柴油机故障诊断技术
2012-03-16司爱威冯辅周饶国强
司爱威,冯辅周,饶国强
(装甲兵工程学院 机械工程系,北京 100072)
模式识别是故障诊断的关键技术和环节,关系到故障诊断的成败.然而,不管采取何种故障模式识别方法,都不可避免地存在误判的问题.对于仅有一种故障模式的故障诊断问题,就有将故障判为正常和将正常判为故障两类误判形式,而两类误判在实际应用中所造成的损失是不同的,一般情况下,将故障判为正常所造成的损失比将正常判为故障所造成的损失要大[1].
支持向量机理论现已广泛应用于模式识别,但该理论没有考虑两类误判在造成损失上的差异.决定分类结果的最优分类平面实际上蕴含着这样的信息:在最优分类面上的样本成为各类别的概率是相同的,而损失是不同的.本文结合诊断中两类误判具有不同损失的特点,对支持向量机最优分类面进行重新设计,并成功应用于柴油机故障诊断.
1 SVM基本理论
支持向量机是从线性可分情况下的最优分类面发展而来的,基本思想可用两维情况来说明.在图1中,十字点和圆点分别表两类样本,H为分类线,H1和H2分别为过各类中离分类线最近的样本且平行于分类线的直线,它们之间的距离叫做分类间(margin).所谓最优分类线就是要求分类线不但能将两类正确分开(训练错误率为零),而且使分类间隔最大[2-3].
设有个线性可分样本{(Xi,Yi)},i=1,2,3…n,xi∈Rm,其中n为训练样本个数,Rm为m 维线性空间,m为训练样本的维数,Yi∈{-1,+1}为类别标号,满足:

式中:ω为分类线的法向向量;b为其截距.此时分类间隔等于2/‖ω‖,使间隔最大等价于使‖ω‖最小或者‖ω‖2最小.满足式(1)条件使‖ω‖2/2最小的分类面就叫做最优分类面,把过两类样本中离分类面最近的点且平行于最优分类面的超平面称为H1和H2,则H1和H2上的训练样本点就是使式(1)中等号成立的那些样本,它们被称作支持向量[4].
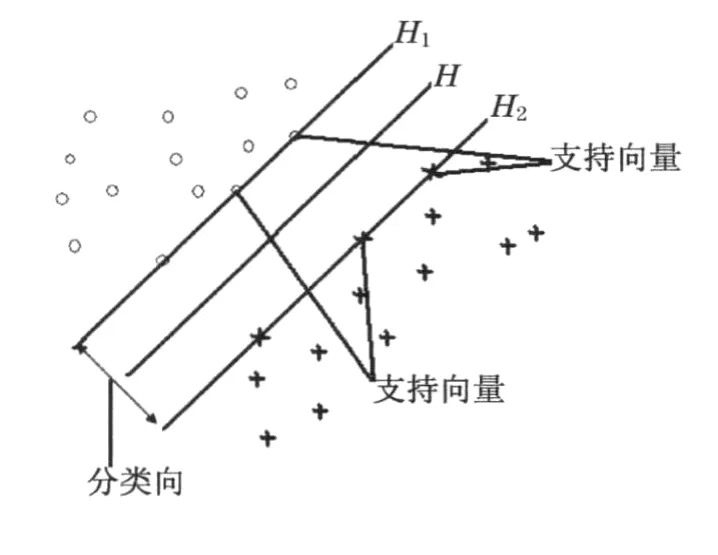
图1 支持向量最优分类面Fig.1 Optimal classification face of support vector
这样,求最优分类面的问题就可表示为:在式(1)的约束下,求下列函数的极小值(最小化泛函):

为此,定义Lagrange函数如下:

式中:αi≥0,为Lagrange系数,这里的目标是将式(3)对ω和b求Lagrange函数的极小值.将式(3)分别对ω和b求偏微分并令它们等于零,就可把上述式最优分类面问题转化为其对偶问题,即

在式(4)的约束下对αi求解下列目标函数的最大值:

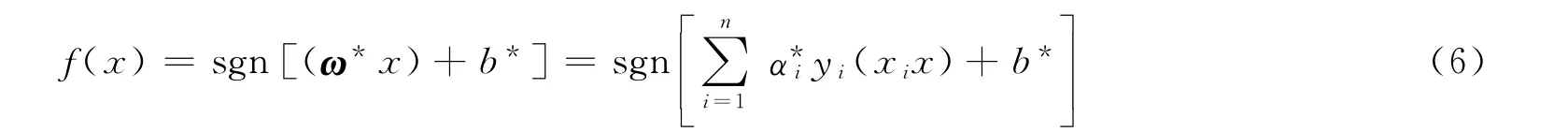
式中:ω*为最优分类线的法向向量;b*为其截距.判别函数f(x)的正负号可判定待分所属的类别,这就是支持向量机.
对非线性可分样本,通过非线性映射Φ将样本从原空间Rm映射为某高维空间中的线性问题,然后在高维空间中求最优分类面.根据泛函理论,一种核函数K(xi,xj)只要满足Mercer条件,就对应某一变换空间的内积,即K(xi,xj)=Φ(xi)Φ(xj).在引入核函数后,支持向量机对应的最优分类面方程为

所以对于给定的测试样本,支持向量机分类器的最优分类函数为

同样,通过判别函数f(x)的正负号来判定待分所属的类别.
2 可变风险的最优分类面设计
利用SVM模型进行故障模式识别时没有考虑两类误判在造成损失上的差异,即两类误判风险相同,这显然是不合理的,所以将对最优分类面进行重新设计,使两类误判的风险可结合实际情况和专家经验调节控制.
考虑图2,结合上面的讨论可以看出:由于支持向量的存在,对于检测样本x,如果存在判别函数f(x)≤-1或f(x)≥1,则可对其给出明确的诊断结果


图2 f(x)与诊断决策关系示意图Fig.2 Relation of f(x)and diagnosis decision
而在区间 -1<f(x)<1特别是在f(x)=0的邻域内,诊断的结果存在一定的不确定因素,将该区域称为可疑诊断区.为了定量描述可疑诊断区诊断结果的不确定性程度,现引入诊断可信度函数.
定义诊断可信度T(x,y)是衡量将当前运行状态x诊断为y的可信程度.显然,对于两类诊断问题{正常1;故障-1},对任一诊断样本都有

考虑到支持向量对诊断结论的支持及分界面的含义有
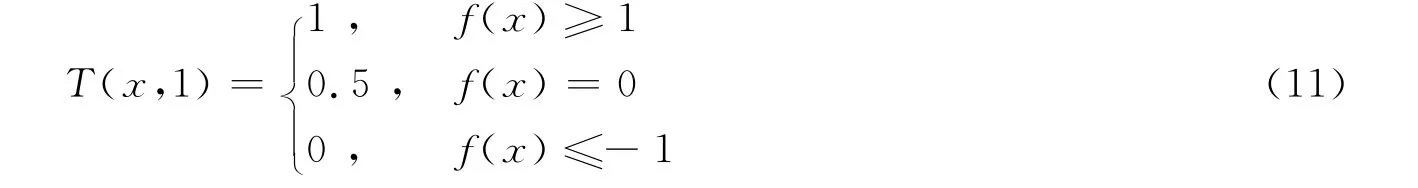
结合式(10)和式(11),可以定义一种诊断可信度函数,如图3所示.具体表达式为

图3 诊断可信度函数Fig.3 Diagnosis reliability function

基于在分类面处两类误判所造成的损失应该相等的考虑,分类面应位于可疑诊断区,即x满足 -1<f(x)<1,同时满足

式中:L1为将故障判为正常所造成的损失;L2为将正常判为故障所造成的损失.
设满足式(13)的分类面方程为

由图2有比例关系

由式(7)、式(10)—(12)可以得到

因此,此时所求分类面的方程变为
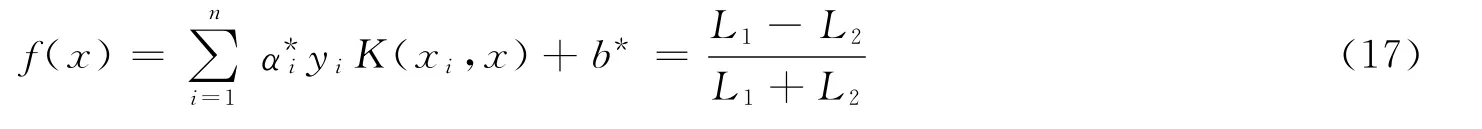
综合以上讨论,可总结在故障诊断中应用SVM算法的步骤为:① 选择合适的核函数,建立优化方程;② 求解优化方程,获取支持向量及与之对应的ai;③由优化方程获得一般意义下的最优分类面f(x)=0;④ 由式(17)建立适合故障诊断需要的分类面f(x)=(L1-L2)/(L1+L2).
考虑两类特殊情况:①L1=L2,此时分类面为f(x)=0,与一般意义下的最优分类面相同;②L1≫L2,此时的分类面为f(x)=1.直观上的解释是将正常误判为故障所造成的损失远比将故障误判为正常的小,因此,这时将可疑诊断区的样本全判为处于故障状态.
3 柴油机故障模式识别实例
3.1 柴油机故障参数设置
本论文选取的诊断对象为东风EQ2102汽车柴油机的机械运动副,包含5种技术状态,其配合参数设置如表1所示.

表1 东风EQ2102汽车柴油机故障参数设置Tab.1 Diesel engine fault parameter setting of Dong Feng EQ2102vehicle
3.2 加速振动信号的采集
在发动机加速或减速过程中,其故障现象表现更明显,这是汽车维修专家所形成的共识,即在非稳态运转条件下的部件,产生更强烈的激励,更易于判别其故障状态[5].
为了能捕捉到载有发动机曲轴轴承明显特征的振动信号,需要记录加速过程中某一转速范围内、某特定部位的振动信号.为此本实验设计了定转速非稳态数据采集系统,随时监测加速过程中的发动机转速,一旦达到预先设定值,立即启动信号采集器开始数据采集.
本实验振动传感器放置位置如图4所示.加速过程中数据采集器的启动转速分别为:800,1300,1800,2100r·min-1.采样频率为25600Hz,采样点数为16384.

图4 加速度振动传感器放置位置Fig.4 Locations of accelerative vibration sensors
3.3 故障识别过程
对采集到的信号进行小波包自回归谱(Wavelet Packet-Auto Regressive Spectrum,WPAR)分析,可知故障信号小波包AR谱分析后的2,3,4频段能量最能反映实际的技术状态,而曲轴轴承异响和连杆轴承异响有三个共同的最佳诊断部位,即油底与缸体接合处第三缸右侧(D),油底与缸体接合处第三缸左侧(E)和第三缸油底下部(F)[5].为了利用更多的故障信息以取得更好的诊断效果,本文分别选取D,E,F三处加速振动信号进行小波包AR谱分析后的2,3,4频段能量作为特征参数,作为SVM模型的输入.
由于该问题是多类分类问题,所以本文选用“1对1”的成对分类算法来建立多类故障分类器.对应5种技术状态共建立10个两类分类器:SVM12,SVM13,SVM14,SVM15,SVM23,SVM24,SVM25,SVM34,SVM35,SVM45(SVMij代表第i种技术状态与第j种技术状态之间建立的SVM).
依据把故障状态误判为正常状态所造成的损失大于把正常状态误判为故障状态所造成的损失、把严重故障状态误判为轻微故障状态所造成的损失大于把轻微故障状态误判为严重故障状态所造成的损失的原则,根据专家经验,估计5种技术状态两两之间误判所造成的损失如表2所示,其中Lij表示把第i种技术状态误判为第j种技术状态所造成的损失.在表2中,Lij(i>j)代表着式(17)中的L1,Lij(i<j)代表着式(17)中的L2.

表2 五类故障诊断风险决策表Tab.2 Risk decision of five faults diagnosis
由式(17)和表2即可求得以上建立的10个两类分类器的分类面方程,结果如表3所示,其中fij(x)=d表示第SVMij个分类器的分类面方程.

表3 10个两类分类器的分类面方程Tab.3 Classification face equations
首先选取10个训练样本,每种技术状态对应2个样本,见表4所示.表4中 ED4,1,ED4,2,ED4,3,EE4,1,EE4,2,EE4,3,EF4,1,EF4,2,EF4,3分别表示 D,E,F三处加速振动信号进行小波包 AR 谱分析后的2,3,4频段能量.
将5种技术状态两两组合的2个训练样本作为对应分类器的输入,对10个两类分类器进行训练,所有分类器均采用高斯径向基核函数,惩罚系数C=1,核参数σ=0.5,所有10个模型训练完毕后,将每种技术状态的2个检验样本(如表5所示)输入训练好的SVM模型,由10个SVM模型分别对10个检验样本进行识别,得到表6的识别结果.
从表6中可以看出,依据多数原则得到的SVM模型的综合输出结果完全符合实际的技术状态,这表明SVM模型可以准确地判断柴油机机械部分的故障模式.

表4 SVM模型训练样本Tab.4 Training samples of SVM (mV)2

表5 SVM模型检验样本Tab.5 Testing samples of SVM (mV)2

表6 SVM模型检验结果Tab.6 Recognition result of SVM
4 结论
(1)基于可变风险SVM模型模式识别算法,充分考虑了各类误判造成的损失,更适宜故障诊断.
(2)在故障模式特性比较简单的情况下,采用可变风险支持向量机与普通支持向量机分类会有相似的效果;但当分类特性比较复杂时,根据专家估计的实际风险,可变风险支持向量机能更充分显示其优越性.
[1]肖建华,樊可清,吴今培,等.应用于故障诊断的SVM 理论研究 [J].振动、测试与诊断,2001,12(4):258-262.XIAO Jianhua,FAN Keqing,WU Jinpei,et al.The SVM theory study applying in fault diagnosis[J].Journal of Vibration,Measurement & Diagnosis,2001,12(4):258-262.
[2]CRISTIANINI N,SHAWE T J.An introduction to support vector machines[M].Cambridge:Cambridge University Press,2000.
[3]HSU C W,LIN C J.A comparison of methods for multiclass support vector machines[J].IEEE Transactionson Neural Networks,2002,13(2):415-425.
[4]鄂加强.智能故障诊断及其应用 [M].长沙:湖南大学出版社,2006.E Jiaqiang.Intelligent fault diagnosis and its application[M].Changsha:Hunan University Press,2006.
[5]肖云魁.汽车故障诊断学[M].第2版.北京:北京理工大学出版社,2006.XIAO Yunkui.The automobile fault diagnosis[M].2nd ed.Beijing:Beijing Institute of Technology Press,2006.
