基于浙江省犯罪率多变量权重的算法研究

2012-03-15付艳茹

中国人民公安大学学报（自然科学版） 2012年3期

付艳茹，马强

（浙江警官职业学院，浙江杭州 310018）

0 引言

犯罪率是比较不同时空条件下犯罪严重程度的常用指标，即犯罪密度。虽然犯罪行为的界定是一致的，但研究与比较犯罪密度往往受到一定条件的限制，其统计分析多以SPSS、SAS软件固有的模型为主，它过多地依赖于现存数据而缺失动态建模及预测的功能，未能有效涵盖影响犯罪率的多项相关变量以及量化相互间的权重关系。国内已有一些文献针对犯罪率问题采用了定量分析，但准确度与适应性仍不及MATLAB的动态建模。

本文基于浙江省犯罪率的角度来探析影响犯罪率的相关变量，通过采用MATLAB平台下的动态建模与仿真实测，对影响犯罪率的多项相关变量进行结构性测定及权重分布进行分析，寻求涵盖权重不同及影响犯罪率多变量（包括城市化率、失业率、客运量、人均GDP、城市基尼系数、农村基尼系数、失业率等主成分）的较高精度犯罪率算法模型。

1 犯罪率多变量权重算法与模型设计

1．1 犯罪率相关变量分析

以MATLAB仿真平台对犯罪率动态建模涉及了影响犯罪率的多项相关变量，国内一般实证研究犯罪率的文献所涉及的相关变量是众多的，如收入分配、劳动力市场环境、社会环境、教育影响、城市化率、失业率、贫困率、人口结构、经济增长、工资水平、通货膨胀、司法质量等［1－3］，国外则包括了更为广泛的、与经济周期相联系的犯罪率变量定义，如合法就业机会、犯罪机会、毒品与酒类物品消费、司法体系运作等［4］。然而，如果在算法模型的实测中，引入以上与犯罪率全部相关的变量，则将会因重叠的信息量大而导致冗余，发生严重的多重共线性问题，其结果是极大地限制了犯罪率模型的实际应用。

考虑到犯罪率与经济相关的变量表现的显著性，将经济增长水平、城乡收入差距、城市化水平、失业率高低等设定为研究犯罪率的相关变量。以浙江省为例，城市化率、人均GDP、恩格尔系数、客运量等经济指标在改革开放的三十年间持续呈现了增长势头，高速推动了“三化”（工业化、城市化、市场化）的进程，繁荣了区域经济，吸引了省外高达1182万人的劳动力流入，外来人口占浙江省现有常住人口5442．69万人的21．7%，城市犯罪问题的滋生与蔓延面临着更为错综复杂的局面，犯罪率持续攀升，至2008年年底，浙江省在押罪犯数量已经上升为国内第2位。受篇幅所限，表1列出了1988～2007年的犯罪率样本数据及部分相关变量指标［5］。

依据表1所列犯罪率样本数据及相关变量指标，基本能概括相应的犯罪率趋势，并可发现浙江省于1988～2007年二十年间的犯罪率、城市化率、失业率、客运量、人均GDP及全国犯罪率的指标值居于总体上升的性态。考虑到影响犯罪率的关联因素是众多的，不同权重的变量指标对犯罪率的影响是不同的，如犯罪率数据样本临近点的阈值及犯罪率相关变量的权重分布等，在不同的经济条件地区将存在一定的差异，而由于犯罪形成的过程是一个未知且动态变化的开放域，若采用经验值来单纯替代，将使得具体的定量受限。因而，可进一步在MATLAB平台下编程实测进行仿真，并基于较大的犯罪率样本数据而获取多个相关变量指标间的联系及量化值。图1是在MATLAB平台下编程实测得到的浙江省城市化率、失业率、客运量、人均GDP、城市基尼系数、农村基尼系数、城乡收入比值、犯罪率共8个相关变量指标的仿真曲线图。研究发现，诸多相关变量指标除个别年份偶有波动外，总体上均处于上升的趋势，呈现出与犯罪率之间的正相关性态。

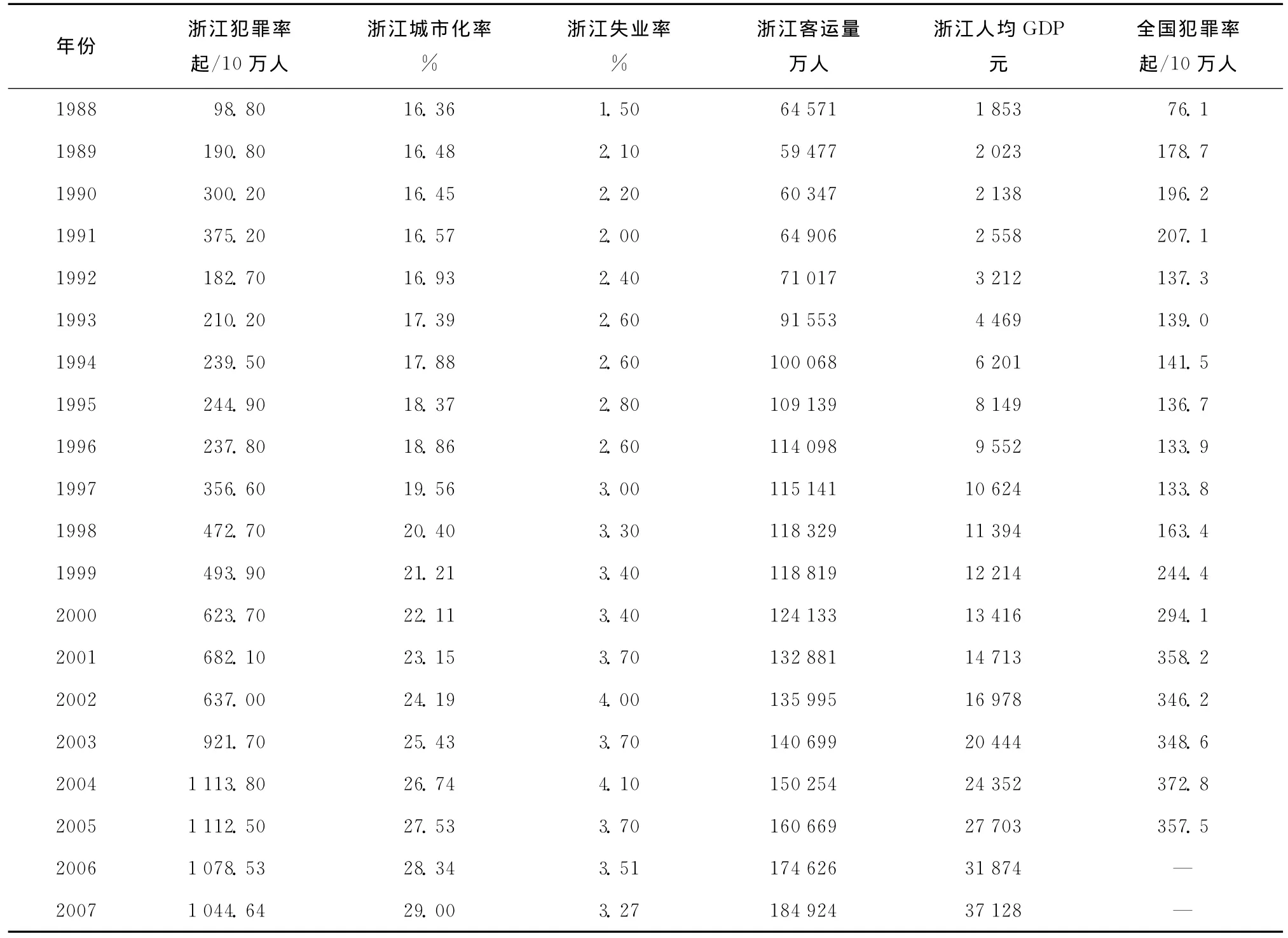
表1 1988～2007年浙江省犯罪率及相关变量表

1．2 犯罪率相关变量的关联度

影响犯罪率的各相关变量在犯罪形成过程中的作用各有强弱，且可能内含的信息量彼此重叠，一定程度上制约了犯罪率模型的准确程度。当定量分析较大的犯罪率样本数据及关联度时，可用实测的手段获取犯罪率相关变量指标内在的联系及量化值，通过仿真图观察各相关变量对犯罪率的影响趋势。在数学意义上，关联度可以考察2个变量数列的相近程度，其值的大小与2个变量数列相互影响程度的大小成正比，关联度越大，说明2个变量数列相互影响的程度越大。在MATLAB仿真平台下，可以编程实测犯罪率各相关变量的关联度，其算法步骤为：

第1步，对犯罪率各相关变量进行初始化处理。即对不同时刻的犯罪样本统计数据构成参考序列：

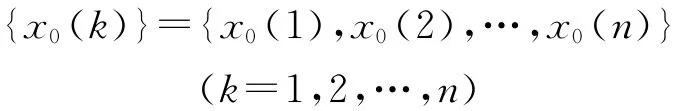
择其对应的比较序列为：

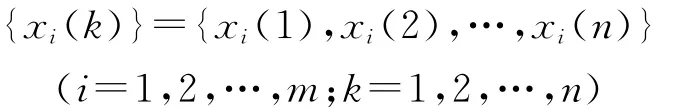
第2步，按指定的分辨系数P，计算犯罪率各相关变量的关联系数

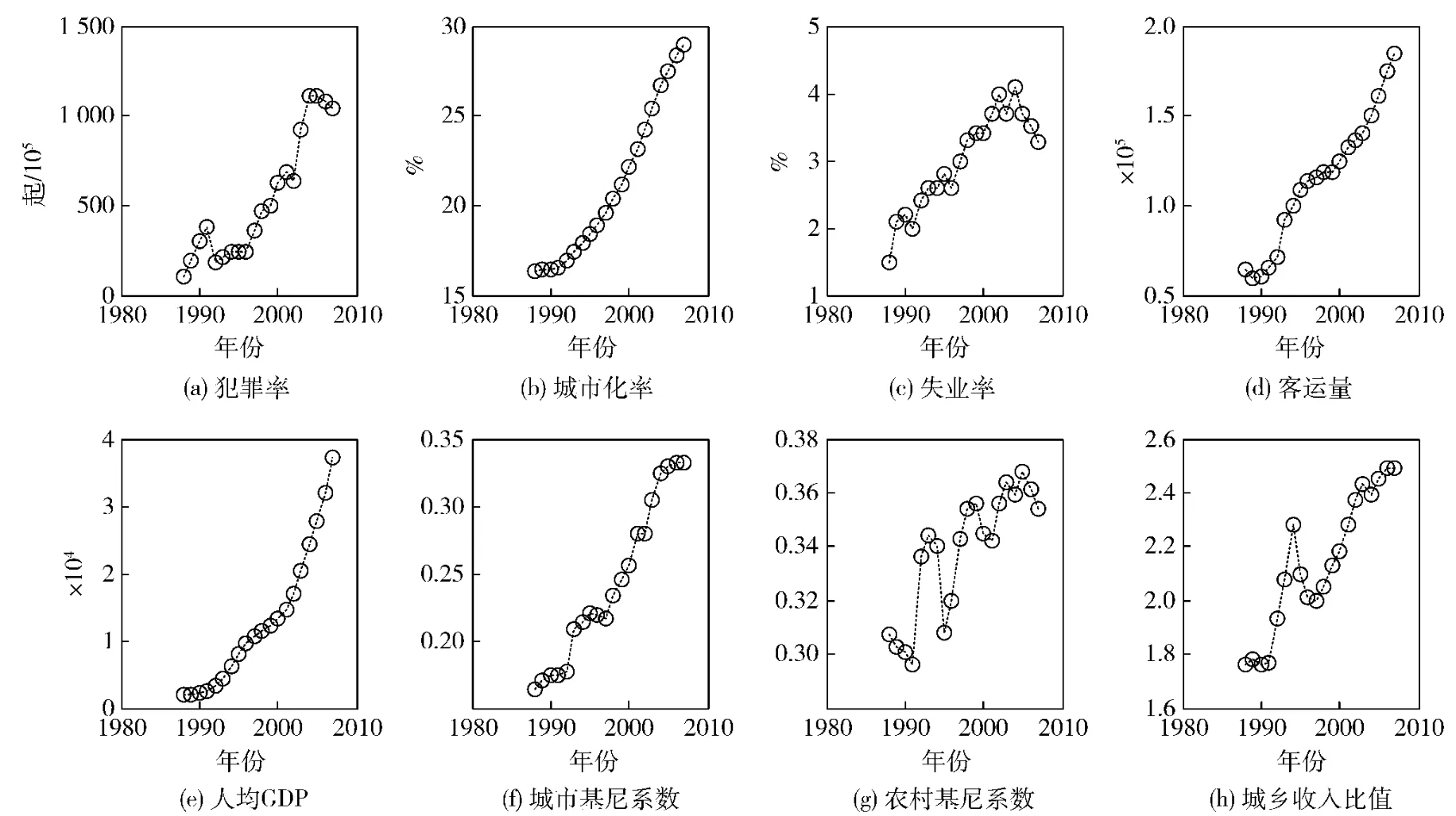
图11988～2007年浙江省犯罪率及相关变量曲线图

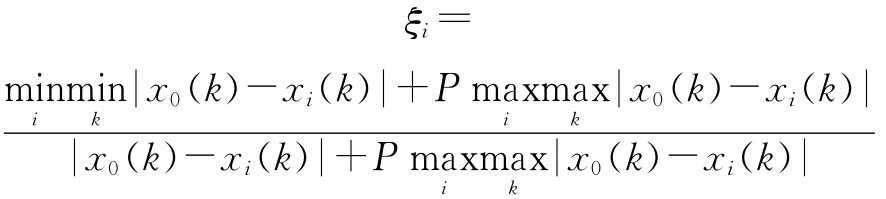
第3步，计算犯罪率各相关变量的关联度

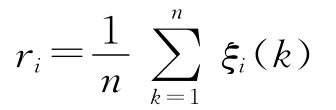
针对以上所设计的算法，可在MATLAB仿真平台下编程实测，其主要的示意代码如下：

在以上MATLAB源代码中，p为所选择的分辨系数，delta＿min为数据初值，incidence＿coefficient为关联系数，r为关联度。仿真实测后，获得了各相关变量与犯罪率的相关度，其从大到小的排序依次为人均GDP（0．7415）、失业率（0．6755）、客运量（0．6509）、城市基尼系数（0．6322）、城市化率（0．6202）、城乡收入比（0．6196）、农村基尼系数（0．6130）。可见，与犯罪率相关度最高的相关变量是人均GDP，其次依次为失业率、客运量、城市基尼系数，而城市化率、城乡收入比及农村基尼系数列后三位。单纯观察相关度的权值分布可以发现，多数变量与犯罪率的相关度差异是不大的，对犯罪率的影响权重大体相当。

为比较犯罪率各相关变量间彼此重叠的信息量，可由MATLAB编程仿真实测出犯罪率各相关变量城市化率、失业率、客运量、人均GDP、城市基尼系数、农村基尼系数、城乡收入比值间的相关系数，其值大小表示了内在的联系程度，见表2。

结合1988～2007年的犯罪率样本数据（表1），考察犯罪率各相关变量间的相关系数（表2），可以发现，各变量间的相互关系均较密切，任意2个变量间的相关系数均较高。仅以城市化率与人均GDP为例，二者间相关系数高达0．9869（其实1979年以后城市化进程与犯罪率就表现为极高的相关性［6］），即使在关系最弱的人均GDP与农村基尼系数之间，其相关系数亦达到了0．7421，可见犯罪率与其相关变量之间呈现显著相关的性态，它表明若将影响犯罪率的相关变量直接对犯罪率进行多元回归，非互斥的变量间的高度相关性将导致大量的信息重叠，对犯罪率的影响权重差异也可能很大，致使所得犯罪率回归模型精度大为降低，不宜实际应用，故需要施加必要的算法改进。

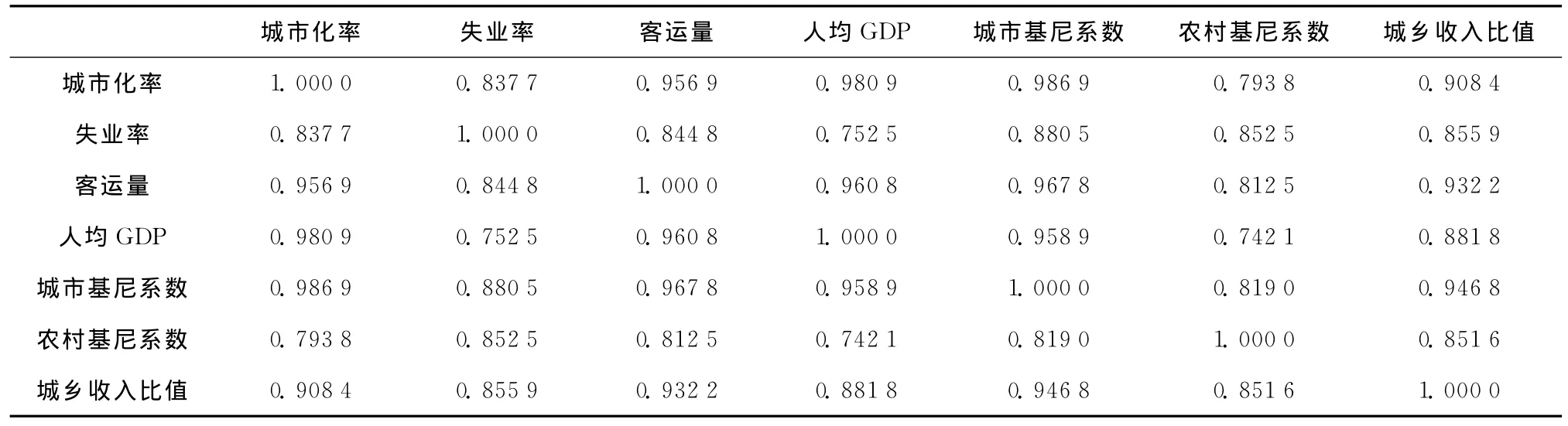
表2 犯罪率各相关变量间的相关系数

1．3 犯罪率各相关变量的主成分分析及模型实测

为避免多信息量相互重叠导致各因素间的高度共线性，准确把握各因素对犯罪率影响的权重，客观地反映各因素对犯罪率的影响程度，可采取主成分分析算法，并在MATLAB平台下编程实测，以便对影响犯罪率的多项相关变量进行结构性测定，通过权重分析来获取客观反映各变量影响犯罪率的量化结论。

有关MATLAB仿真实测犯罪率各相关变量主成分分析的示意代码如下：

在以上MATLAB源代码中，仿真功能的实现借助了矩阵的标准化变换与主成分分析程序的调用，其中stdr表示各变量的标准差，p3是前3个主成分系数，score是前3个主成分得分，egenvalue是特征值，per是各个主成分的贡献率。程序运行后，可获得涵盖总信息量97%以上的3个主成分如下：

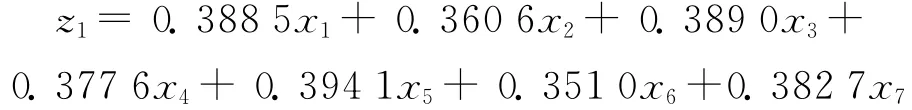
在此基础上，实测出的主成分特征向量为：

进而得到相应的犯罪率模型为：

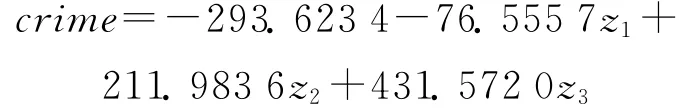
分析仿真实测结果可以发现，第一主成分的特征值为远大于1的6．3020，其贡献率高达90．03%；第二主成分的贡献率为5．63%；第三主成分的贡献率为2．20%。前3个主成分的累计贡献率达到了97．86%。

其中，以第一主成分最为重要，它基本涵盖了7个变量的所有信息，对犯罪率的变化影响是最大的，它内含了影响犯罪率90%以上的信息量，而影响犯罪率的另外7个变量，如城市化率、失业率、客运量、人均GDP、城市基尼系数、农村基尼系数、城乡收入比值等，其权重分别为0．3885、0．3606、0．3890、0．3776、0．3941、0．3510、0．3827，相对而言，各变量的权重差距不显著，说明对犯罪率的影响程度彼此相差不大，而权重稍大些的城市基尼系数0．3941、客运量0．3890、城市化率0．3885、城乡收入比值0．3827，与犯罪率关系均较为密切；第二个主成分的贡献率是5．63%，其中较大权重的是农村基尼系数0．6260、失业率0．4943，人均 GDP0．4710等3个变量；第三个主成分的贡献率为2．20%，其中权重最大的是失业率为0．7280，其次为农村基尼系数0．6293，这2个变量足以体现第三个主成分。从总体上而言，犯罪率与各因素的相关度分布及各因素对犯罪率的权重分布皆较均衡，并无明显差异。如果根据3个主成分z1、z2、z3的得分，并用其贡献率进行加权，则可计算出犯罪率的总得分如下：

同时，可在对应1988～2007年犯罪率样本数据（表1）的基础上，以排序方式获得相应的总得分水平（表3），由该表可印证1988～2007年二十年间的犯罪率总体上升的结论。

表31988～2007年浙江省犯罪率得分及排序

在此基础上，进一步利用MATLAB对量化的准确性进行验证，即根据3个主成分所建立的犯罪率模型对1988～2007年二十年间的浙江省犯罪率进行仿真实测，以得到相应的犯罪率测试值Crime＿yc及对应的相对误差Crime＿ycwc：

分析相应的数据可知，采用3个主成分进行测试后，其结果均已很好趋近于实际值。以表1中的2007年犯罪率为例，犯罪率的实际值为1044．6起／10万人，而算法模型的测试值为1124．3起／10万人，二者已经极大地趋近，基本符合实用要求。观察测试的相对误差，只有3个采样点的相对误差较大，分别为0．43301、0．36835、0．45933，而60%以上的点的相对误差均在0．1以下，可见经主成分分析后的回归效果较好。在实际操作中，基于第一个主成分的贡献率高达90．03%，说明完全可以略去后两个主成分，此时，犯罪率模型的算法精度可以得到足够的保证。