基于EDAPO优化算法的配电网重构

王黎，苏丹，王兴伟

(1.华北电力物资公司，北京100075;2.华北电网有限公司，北京100053;3.大庆市供电公司，黑龙江大庆163458;4.东北电力大学电气工程学院，吉林吉林130012)

配电网具有闭环设计、开环运行的特点，它含有大量的常闭开关和少量的常开开关。其中，配电沿线上设有分段开关，馈线入口设有联络开关。正常运行的网络是通过调度员的开关操作调整网络结构。对于配电网开关分合的操作，是有效降低网络损耗、平衡负荷，消除过载及提高电压质量的重要手段［1］。

配电网重构需要优化大量的开关，是非线性组合优化问题，在目前求解算法中主要有以下几类:(1)传统的数学优化算法，该算法随着维数的增加存在严重的“维数灾”问题，难以实际应用;(2)启发式优化算法，主要有最优流模式法和支路交换法，虽然计算速度有了很大的提高，但缺乏数学意义上的全局最优解;(3)人工智能优化算法，如遗传算法、禁忌搜索算法、免疫算法等，它们在全局寻优方面存在网络参数变化和计算速度等问题。而配电网呈辐射状，故求解过程中可能生成不可行解，为了解决上面的问题本文提出了一种基于分布估计的离散拟态物理学优化算法。

1 建立配电网重构的数学模型及约束条件

配电网优化重构是在满足网络运行约束条件下，通过开关的开合操作达到降低网络损耗的目的。因此，以网损为重构的目标函数式:

式中:F为网络重构的目标函数;N为系统支路数;kb为支路开关的开合状态，kb为1表示该支路开关闭合，为0表示该支路开关打开;rb为支路的b电阻;Pi、Qi、Vi分别为支路b的有功功率、无功功率、支路末端节点电压幅值。

配电网重构需满足下列的约束条件:

(1)潮流约束(等式约束)

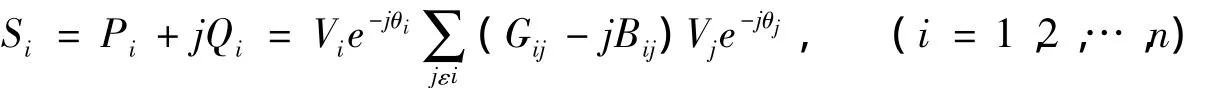
按实部、虚部展开，可得:

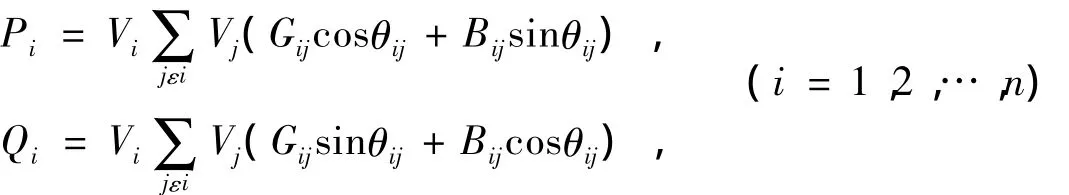
其中:θij=θi－θj。式中:Pi、Qi分别为节点i输入的有功和无功功率;Vi、Vj分别为节点i、j的电压;Gij、Bij为支路b的电导和电纳;θij为支路b两端的相角差。

(2)电压、容量约束(不等式约束)

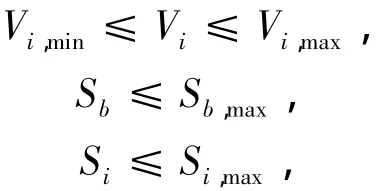
式中:Vi，min、Vi、Vi，max为节点电压、极其上下线;Sb、Sb，max为支路流过的功率及最大允许值;St、St，max为变压器流出功率及最大允许值。

(3)网络拓扑约束

1)网络结构中不能出现孤立节点，即所谓的“孤岛”;

2)根据配电网“闭环设计、开环运行”的特点重构后的网络必须为辐射状。

2 基于EDAPO算法的配电网重构

2.1 算法介绍

拟态物理学优化算法(artificial physics optimization，APO)是一种新的基于群体的随机搜索算法。最早是由Spear和Cordon提出的一种基于群体随机搜索的智能优化算法，该方法简单、易于理解，它是对牛顿第二定律(F=ma)的一种模拟，“拟态”也因此得名，通过个体间的虚拟力作用改变个体的速度和位置，达到收敛于全局最优解周围［1－2］。与传统遗传算法及PSO算法相比，APO算法具有稳定和快速收敛的优点以及较好的鲁棒性。APO算法主要用在在解决决策变量为实数的优化问题。算法中每个个体是解空间中的一个可行解，每个个体根据自己的惯性及其他个体的合力作用来调整自己的运动，这类似于粒子群中的“粒子”运动。整个群体所经历的最好位置就是目前找到的全局最优解，而个体的好坏由优化问题的适应值来评价。APO群体中第d维的位置表示为xi，d，第d维的速度用vi，d表示，受到第j(i≠j)个个体的虚拟力为Fij，d，受到群体中所有其他个体总的作用力为Fi，d。因此，拟态物理学优化算法的表达式如下:

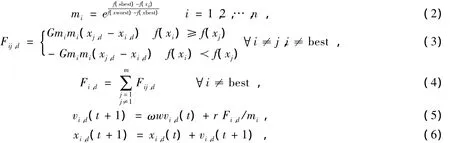
其中:n为群体规模;ω是惯性权重取值从0.9递减到0.4;G是引力因子，因为ω初值较大，为了更好的平衡局部和全局最优本文取G=10;r是一个在(0，1)内的随机数，服从标准正态分布，这样可以增加种群多样性。

拟态物理学优化算法虽然在全局搜索上优于粒子群优化算法，但改善程度有限，本文将分布估计的理论引入到拟态物理学优化算法中，利用分布估计的概率向量P及对新生成个体以一定变异率α实施按位变异，在算法优化后期摆脱算法陷入“早熟”，改善全局收敛效果［2］。分布估计是选择所有个体最优值，建立优质解的概率模型，新种群的生成是由两部分组成，即概率模型部分和至今的最优信息。在EDA(Estimation of distribution algorithm)概率模型的选择中，本文采用被广泛应用的UMD(Univariate marginal distribution)模型，并采用简单的一阶统计量UMD建立模型。pd表示粒子第d维取值为1的概率，在新种群的产生过程中，以大概率β=0.9抽样产生新解。以小概率1－β直接复制全局最优解作为新的解。

具体如下式:

rand()为［0，1］区间随机数。参数β控制新解的产生。概率向量初始化如下式:

迭代中概率的更新如下式:

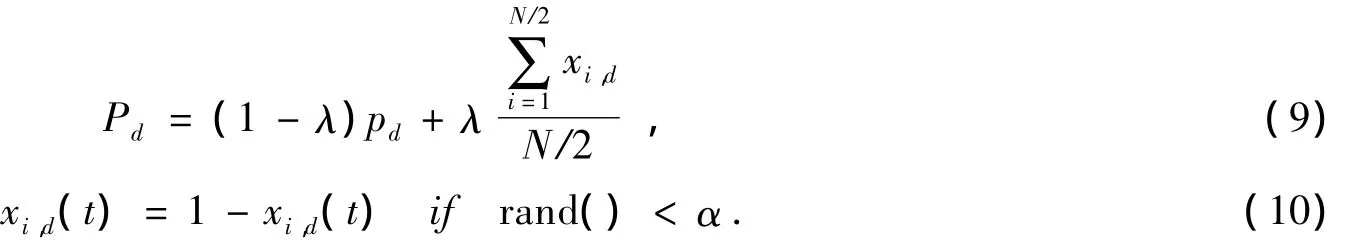
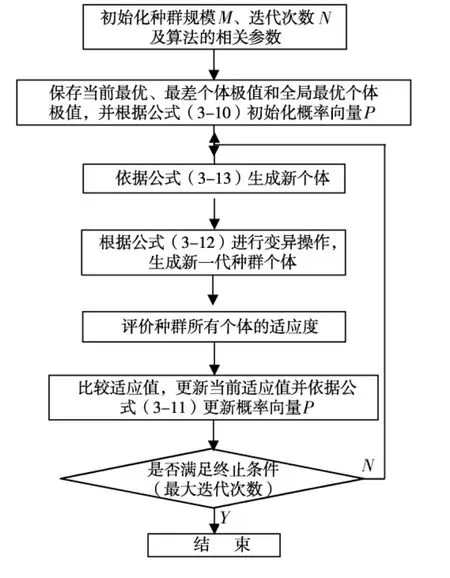
2.2 算法步骤

基于分布估计的离散拟态物理学优化算法的重构流程图:

2.3 算法分析

拟态物理学优化算法在形成个体质量的过程中不仅考虑了所有个体经历的最好适应值，而且考虑了个体经历的最差适应值，因此在形成质量的过程中就极大的避免了个体的“早熟”现象发生，而算法在速度公式中的随机数采用正态分布取值，提高了算法的种群多样性，避免算法陷入局部最优。文献［6］［7］的实验也证明了该算法在全局收敛和稳定性上较粒子群算法更优越，而为了在全局收敛上有更好的效果，本文在拟态物理学的基础上引入广泛采用的分布估计算法，应用其中的概率向量和变异率而更好的避免算法陷入局部最优。

实验表明在粒子群算法中两个随机数的取值不同和相同对最优化的结果有很大影响，经过MATLAB和Visual Basic语言随机函数实验结果表明当两个随机函数取相同值时粒子群有着更好的优化性能，拟态物理学算法避免了两个随机数的选取，提高了优化性能和效率。

2.4 算法优化过程

对于群体初始化，本文根据配电网闭环结构、开环运行的特点，首先将网络中所有开关闭合，对于环网外层的优化，采用简化的网络，将每个支路“虚拟”成为一个开关，这时按照辐射网，在每个环中打开一个开关，找到打开的支路组合，对于环网内层的优化是将非环网开关闭合，环内按照外层优化后打开的支路，按照每个支路打开一个开关的原则进行优化，这样做不仅使得群体优化计算量大为减少，同时减少相关的潮流计算次数。由于是按照环路生成，也极大的避免了不可行解的产生。对于编码规则，依据开关的两种状态，打开或者闭合，因此选择二进制编码方式更加合适。本文主要采用的编码方式为，对于不在环内的开关不参与编码，缩短编码长度，因为本文采用的是分层优化，这样在简化计算的同时提高了计算速度。

3 算例分析

算例为美国PG＆E69节点单电源馈线系统，该系统中共有73条支路，其中含有联络支路5条，系统的额定电压为12.66 kV，总负荷为3 802.2 kW+j2 694.6 kvar。首先依据网络简化规则，网络中的环为单位分别将网络划分为5个部分。

设定种群规模为30，最大迭代次数为30次，α取值为0.001，β取值为0.9，j取值为0.7，ωmax为0.9，ωmin为0.4，G取值为10，重构后拓扑结构及迭代次数如图1、图2所示。

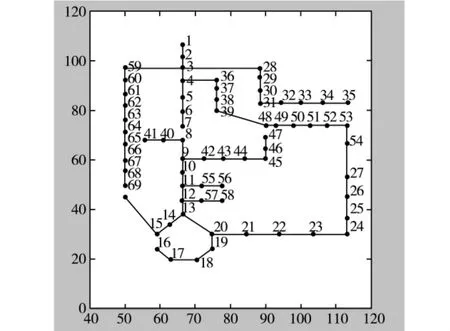
图1 PG＆E 69节点重构拓扑图

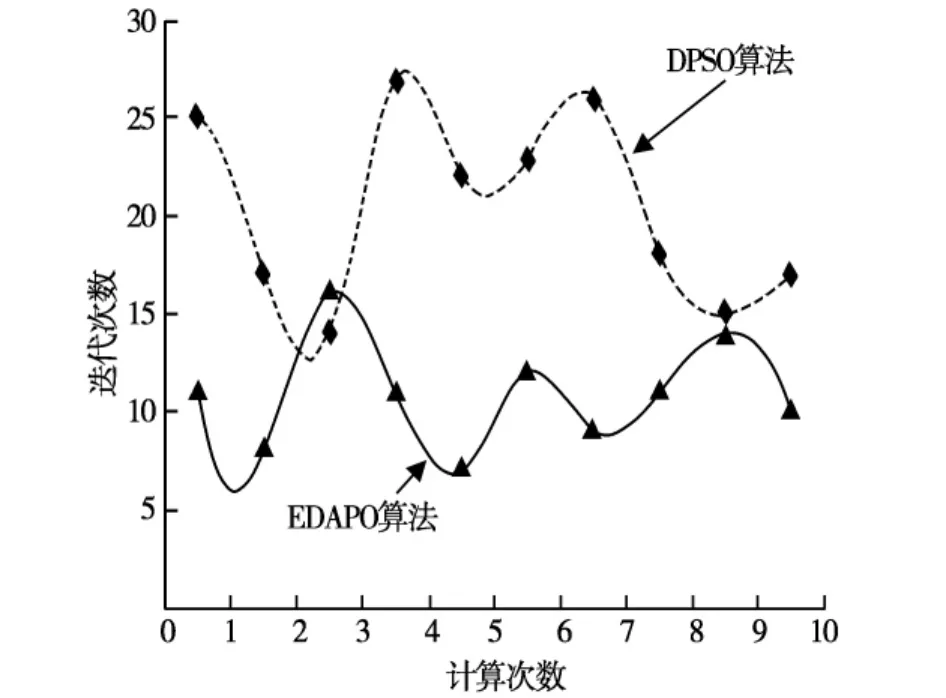
图2 PG＆E 69节点迭代比较图

表1 重构前后的比较结果

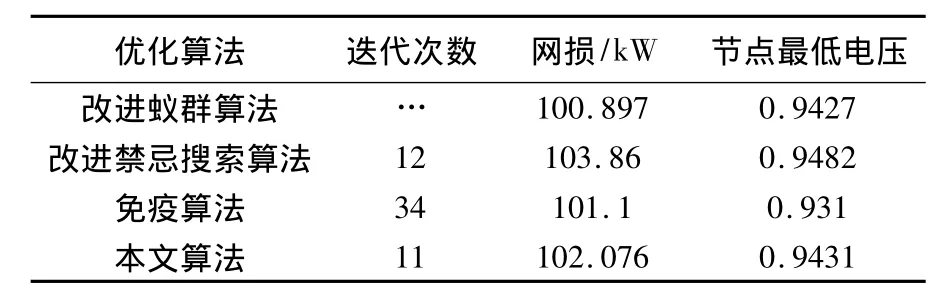
表2 本文算法(EDAPO)与其它算法比较结果

从表1中可以看出，重构前后网络损耗明显降低，节点电压得到明显改善。并且可以看到重构前打开的为联络开关，重构后有3个分段开关替代了联络开关，取得了明显效果，为了进一步验证本文方法的正确性、有效性，现与禁忌搜索算法［3］、改进禁忌搜索算法［4］、免疫算法［5］等算法比较结果如表2所示。

从表2中可以看出，无论是改进蚁群算法、免疫算法在节点电压提高上都略逊于本文算法，在迭代次数上，本文算法明显优于其他算法。而本文算法在网损计算性质方面也与其他算法较接近。因此，纵观三方面的比较结果充分验证了本文算法的有效性和较高的搜索效率。

4 结论

针对以往配电网重构算法研究的局限性，本文通过对APO算法和EDA算法各自优缺点的分析比较将两者有机的结合在一起，提出了一种全新的智能优化算法(EDAPO)。在对配电网络模型的处理过程中，本文引入了克鲁斯卡尔(Kruskal)生成树法，并实现分层计算成功简化搜索步骤，减少程序运行时间，通过对美国PG＆E 69算例分析证明本文方法的离散化处理的可行性。验证了EDAPO算法在配电网重构中应用的正确性，而与其他算法结果进行对比，表明本文算法全局寻优速度快、稳定性好。

［1］李焱，时芝勇，海晓涛.基于改进蚁群算法的配电网重构［J］.陕西电力，2010(9):22－25.

［2］王艳，曾建潮.一种基于拟态物理学优化的多目标优化算法［J］.控制与决策，2010，25(7):1040－1044.

［3］陈根军，李继洗，唐国庆.基于丁bbu搜索的配电网络重构算法IJI.中国电机工程学报，2002，22(10):28－33.

［4］葛少云，刘自发，余贻鑫.基于改进禁忌搜索的配电网重构［J］.电网技术，2004，28(23):22－26.

［5］蒙文川，邱家驹.基于免疫算法的配电网重构［J］.中国电机工程学报，2006，26(17):25－29.

［6］Xie L P，Zeng J C.A global otimization bsed on physicomimetics framework［C］.The 2009 World Summit on Genetic and Evolutionary Computation.Shanghai，2009.

［7］Xie L P，Zeng J C，Cui Z H.Using artificial physics to solve global optimization problems［C］.The 8th IEEE Int Conf onCognitive Informatics.Hong Kong，2009.