基于小波神经网络的饮用水源水水质参数预测模型研究

2012-03-11田考聪

中国卫生统计 2012年3期

邓宇田考聪

小波神经网络

小波分析〔1－3〕(wavelet analysis)是为了克服傅里叶变换的不足而产生的，它能有效地提取信号的局部信息，具有良好的时频域局部化功能，享有“数学显微镜”的美名。人工神经网络〔4－5〕(ANN)具有自组织学习、自适应和容错性等优点，是一类通用函数逼近器，已被广泛用于非线性系统的建模优化，但是传统的神经网络往往存在参数选择易陷入局部最小、收敛速度慢、网络结构设计具有一定的盲目性等缺点，因此将小波变换与神经网络的优点相结合而产生了小波神经网络〔6－7〕(wavelet neural network，WNN)。

按照小波分析与人工神经网络的结合方式，小波神经网络通常可以分为两类〔8〕:一种是辅助式结合，也称为松散型结合方式;另一种是嵌套式结合，也即紧致型结合方式。

所谓辅助式结合，即将小波分析作为神经网络的前置预处理手段，为神经网络提供输入特征向量，然后再用传统的神经网络进行处理，该方法将原始信号的不同频率成分分别用传统神经网络学习训练，产生输出，这样就避免了不同频率成分的信号混杂在一起而增加了网络学习训练的难度(容错能力)，可以取得比较好的效果。

小波分析与神经网络的嵌套式结合，是目前大量研究小波神经网络的文献中广泛采用的一种结构形式，嵌套式小波神经网络与一般的前馈型神经网络(如BP神经网络)一样，其网络结构并没有什么本质的区别，它也采用监督式学习方式，其基本思想是由Zhang Qinghua 和 Benveniste〔9〕于1992 年正式提出的，即用小波基函数来代替常规神经网络的隐含层激励函数，同时相应的输入层到隐含层的权值及阈值分别由小波基函数的尺度参数和平移参数来代替，其结构如图1所示。

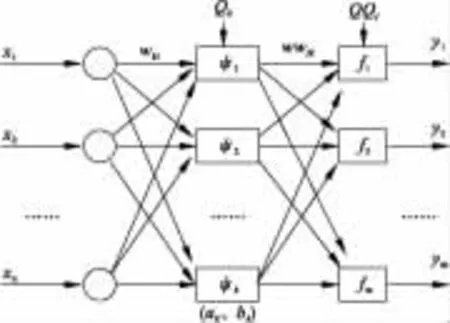
图1 嵌套式小波神经网络结构

本文利用饮用水源水水质参数数据，分别针对小波分析与人工神经网络的两种不同结合方式，建立各自的水质参数预测模型，以探讨两种不同结合方式的小波神经网络在饮用水源水水质参数数据上的预测效果。

应用研究

1．研究数据

选用重庆市某主城区以嘉陵江为水源的饮用水源水2001～2005年高锰酸盐指数月平均浓度作为研究对象。选用2001～2004全年及2005年前6个月高锰酸盐指数月平均浓度作为网络的训练数据，通过建立小波神经网络水质参数预测模型，来预测2005年后6个月的高锰酸盐指数平均浓度值。研究数据如表1所示。我们将此数据看成一个以时间点为横轴的单一时间序列。

2．样本设计

设时间序列 x={xi|xi∈R，i=1，2，…，l}，对于单一时间序列，我们可以通过序列前N个时刻的值预测后M个时刻的值，可以采用序列的N个数据为滑动窗，并将其映射为M个值，这M个值代表在该窗之后的M个时刻上的预测值。这样就把数据分为K个长度为N+M的有一定重叠的数据段，每个数据段可以看成是一个样本，这样可得到K=L－(N+M)+1个样本。可以将每个样本的前N个值作为网络的输入，后M个值作为网络的输出，通过学习使该网络实现从输入空间RN到输出空间RM的映射，从而达到时间序列预测的目的。

表1 2001～2005年重庆某区饮用水高猛酸盐每月监测数据

本文选取滑动窗的大小N=4，输出M=1，由此可得到56个样本，取前50组数据作为训练集，最后6组数据为预测集。预测之前，首先要对数据进行归一化处理，使其落入相应的理想区间，使网络在进行网络参数调整时，调整幅度大，从而加速网络的收敛进程。最后通过反归一化处理，得到最终预测值。

3．辅助式小波神经网络预测模型

目前在众多的神经网络类型中，BP神经网络为研究最多且应用最为广泛，因此选用BP神经网络为辅助式小波神经网络预测模型骨架，实现从输入空间R4到输出空间R1的映射。

小波分析时，选择合适的小波函数对模型的预测精度及泛化能力非常重要，也是关键步骤，但目前尚无实质性的理论指导。而对于最大分解尺度的选择，在一定预测精度要求下，分解尺度既不能太小也不能太大，若尺度选得太小，则不能有效地将原信号中具有不同频率特征的分量分离出来，也就无法得知原序列各频段详细信息，无法体现小波变换的优越性，尺度过大则需要用较多的模型对分解后的各个分量进行预测，各个预测模型都会引入一定的误差，从而导致最终预测误差变大。针对本文研究数据，笔者在参考大量文献资料〔10－13〕后，最终选用db3小波基进行2层小波分解，分解后得到的低频信号和各高频信号及信号重构如图2所示。

图2中，s表示原始信号，即2001～2005年高锰酸盐指数月平均浓度，ca2表示进行2层小波分解后得到的低频概貌分量，可见ca2基本反映出原信号的峰值及变化趋势，为原信号的趋势成分。cd1和cd2为分解后得到的高频信号，其中cd1随机波动，为原信号的随机成分，而cd2基本上呈周期性的波动，为原信号的周期成分或者说季节成分;我们将cd1与cd2对比可知，从数值上讲，cd1比cd2波动幅度大，变化也较剧烈些，这也就是说，原序列s的随机变化强于季节因素对其的影响，而对于随机成分，预测精度再高的模型也很难掌握其变化发展趋势，因此将研究数据不同频率成分分量混杂在一起进行预测，其效果势必不会理想。s1为分解后的重构信号，由图可知:重构信号与原信号相比基本没有什么差别。原信号的分解关系为:s=ca2+cd1+cd2，重构则为分解的逆过程。原信号与重构信号的误差平方根为7.2786×10－12，这说明采用本文所说的分解重构关系是切实可行的。

图2 小波分析数值变化曲线

研究数据经小波分析后，然后用BP神经网络分别对各分量数据进行模拟预测，最后把各分量数据的预测结果进行重构而得到最终预测结果。

4．辅助式与嵌套式相结合的小波神经网络预测模型

原始数据经小波分析可知，研究数据包含较大的随机成分，而随机成分会影响模型对数据的预测效果，因此，考虑到随机成分对模型预测效果的影响，我们基于辅助式小波神经网络结构与嵌套式小波神经网络结构相结合的思想，把辅助式小波神经网络与嵌套式小波神经网络都融合在模型的建立过程中，即先对原序列进行小波分析，提取不同成分的分量，然后对不同分量分别用嵌套式小波神经网络(我们称之为子小波神经网络)进行学习训练，将不同分量的预测输出结果再进行信号重构，得到最终的预测值。

原始数据经小波分析后，各分量的子小波神经网络均选为三层网络结构，其中输入层只负责将各分量数据提供给网络，不参与计算。隐含层激励函数选择墨西哥帽，原因在于墨西哥帽函数在［－1，0］区间为单调递增函数，其导函数在该区间内恒大于零，且导数值较大，在该区间内，墨西哥帽函数具有常规S型函数的曲线特征，因而我们只需把各子小波神经网络的网络参数初始化为［－1，0］区间均匀分布的随机数，同时各分量的样本数据也归一化为该区间，这样就使得各子小波神经网络在运用改进BP算法进行网络参数的调整时，获得较大的导数值，从而网络参数调整幅度大，加速网络的收敛进程。而输出层采用线性激励函数，即把隐含层输出结果通过网络输出层线性加权到网络输出空间。本文最终确定的各子小波神经网络结构如表2所示。

表2 各子小波神经网络最终结构

研究数据经小波分析提取各分量后，我们采用如表2所示的网络结构建立各自分量的子小波神经网络，经学习训练预测后，再把各子小波神经网络的预测结果进行小波重构，而得到最终预测值。

5．预测结果与分析

本文采用Matlab 7.1软件编程建立模型求解。分别用辅助式小波神经网络、辅助式与嵌套式相结合的小波神经网络对研究数据进行预测。采用均方根误差(RMSE)以及平均绝对百分比误差(MAPE)来评价模型最终预测效果，结果如表3所示。图3为两预测模型的最终预测值与实测值的对比图。

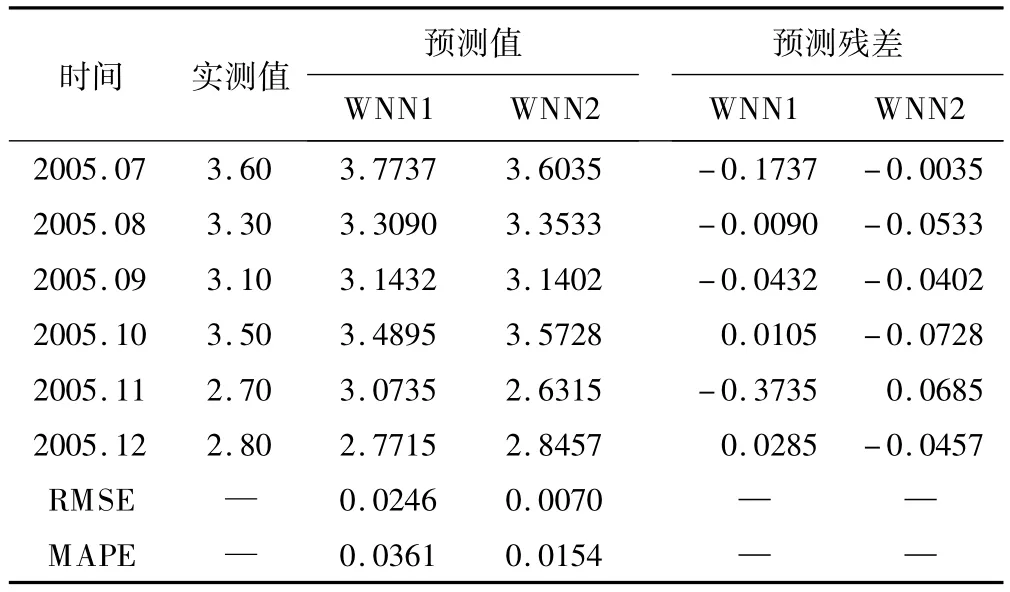
表3 各模型预测比较结果

图3 两个模型预测值与实测值的对比

表3与图3中，WNN1表示辅助式小波神经网络预测模型，WNN2表示辅助式与嵌套式相结合的小波神经网络预测模型，其中图3中，后6个时间点为预测样本，由图和表可知，WNN1与WNN2对研究数据的预测模型效果，表现在 RMSE和 MAPE较小，其中WNN2的预测效果优于WNN1。实例说明，小波神经网络对研究数据预测效果较好，具有很强的学习逼近能力、泛化能力，将其用于水质参数预测、及总体水质评价具有很大的实际应用价值。

结论与讨论

本文应用小波神经网络方法预测饮用水源水水质参数，提出了辅助式与嵌套式相结合的小波神经网络预测模型，由于小波神经网络既具有时频域局部化功能，又具有自组织、自学习能力，其对研究数据的学习逼近能力、泛化能力强，因而取得了较好的预测效果。但在应用小波神经网络方法建模时，应注意以下几个方面:

1．在样本的预处理即样本设计时，应考虑滑动窗大小的选取，不同的滑动窗大小会影响最终的预测精度，一般应选择多组不同滑动窗大小，分别建模预测，然后选择其预测精度最好者。

2．辅助式小波神经网络中小波分析母函数的选取，针对具体信号，选择合适的小波母数是小波分析的关键步骤。确定小波函数质量的依据主要有:函数的支撑长度、对称性、函数的消失矩阵阶数及正则性等等，一般情况下，如果我们希望得到数据信号的一个主要的长期的发展趋势而并不要求对信号进行短期的精确预测时，可选用具有正则性的小波函数;相反如果我们期望得出精确的预测结果，就应选择具有良好紧支性的小波函数。

3．嵌套式小波神经网络中隐含层小波激励函数的选取，选择不同的小波激励函数对网络的收敛速度影响很大，但目前尚无统一理论指导，本文根据改进BP学习算法的基本思想，结合不同小波母函数的曲线特征，选择墨西哥帽小波母函数作为隐含层激励函数，并由此得出网络初始参数及样本数据的理想区间。

4．此外，在运用神经网络方法预测饮用水源水水质参数变化趋势时，最好应先对原数据进行时间序列分析、小波分析等，以分析序列不同成分，如趋势成分、循环成分、随机成分等，从而确定原数据序列平稳性等特点，而往往对于随机成分而言，其预测效果是不十分理想的。后在此基础上，再运用神经网络方法建立模型预测。

1．费佩燕，刘曙光．小波分析应用的进展与展望．纺织高校基础科学学报，2001，14(1):72-78．

2．Daubechies I．Ten lectures on wavelet．Philadelphia．PA:SIAM Press，1988．

3．张德干，郝先臣，徐凌宇，等．基于小波理论的数据挖掘方法研究．小型微型计算机系统，2001，22(8):946-949．

4．周利锋，高尔生，等．人工神经网络的应用．现代预防医学，1998，25(3):272-274．

5．任宏．人工神经网络及其在预防医学领域的应用．上海预防医学杂志，2003，15(1):22-24．

6．薛桂先．神经网络方法在黄河来水预测中的应用．《农业网络信息》研究与开发，2006，5:36-38．

7．匡芳君，等．基于小波神经网络的人力资源评估模型．微计算机应用，2008，29(1):24-28．

8．蒋霖，李向民等．多小波神经网络在变形预测中的应用．山西建筑，2008，34(1):13-14．

9．Zhang Qinghua，Benveniste A．Wavelet networks ．IEEE transactions NN，1992，3(6):889-898．

10．葛哲学．小波分析理论与MATLAB R2007实现．北京:电子工业出版社，2006:31-40．