非标准分布贝叶斯分析的WinBUGS实现*

徐州医学院流行病与卫生统计教研室(221002) 曾 平 王 婷 何 鹏

WinBUGS是一套程序化贝叶斯统计分析软件，应用者只需要指定数据的似然函数和参数的先验分布，然后就可通过Gibbs抽样得到参数的后验样本，这对没有显性表达式的贝叶斯后验分布尤其重要。Win-BUGS软件中提供了23种常见的分布用于指定似然函数和先验分布〔1〕，能够满足大部分的贝叶斯统计分析。然而如果贝叶斯分析中的分布形式超出了Win-BUGS软件所提供的范围，那么需要应用一定的编程技巧和数学转换以适于WinBUGS的程序要求。本文主要介绍非标准分布贝叶斯分析的WinBUGS实现技巧，这里所谓的非标准分布是相对于WinBUGS中的23种分布而言。

原理和方法

1．一个正态数据的WinBUGS程序

假设数据X=xi，i=1，…，n来源于独立的正态分布f(xi|μ，τ)，目的在于通过X对参数μ，τ做出推断。参数的似然函数指定独立的无信息先验 μ ～N(0，10－6)和 τ～gamma(0.001，0.001)，根据贝叶斯定理，μ，τ的后验分布为

f(μ，τ|X)∝L(X|μ，τ)N(0，10－6)gamma(0.001，0.001)需要说明的是:(1)WinBUGS软件中正态分布的参数为均数和精度(precision)〔1〕，即 τ =1/σ2;(2)μ，τ 的标准无信息独立先验应该是μ∝1和τ∝1/τ，都属于不规则先验(improper prior)〔2〕，但 WinBUGS 中不允许指定不规则先验，因此分别指定为 N(0，10－6)和gamma(10－3，10－3)，此时各自的方差为 106和 103，如此大的方差反应了对参数信息的模糊认识，这种先验又被称作局部均匀先验(locally uniform prior)或低信息先验(low informative prior)〔3〕，避免出现不规则的后验分布。对应的WinBUGS程序如下:

model{程序以 model开始所有程序都包含在“{}”中

for i in 1:n{

x［i］～dnorm(mu，tau)}3 ～4 行通过 for循环语句建立似然函数

mu～dnorm(0，1．0E-6)指定 μ 的先验

tau ～dgamma(0．001，0．001)指定 τ的先验

sigma＜-sqrt(1/tau)计算标准差

}

所有的参数或者通过计算得到，如标准差sigma由精度计算得到，或者必须指定一个分布，如对x和mu指定正态分布，对 tau指定 gamma分布，“＜-”的作用和“=”一样，“～”表示“服从某个分布”。Win-BUGS中提供的23种常用分布，见表1。

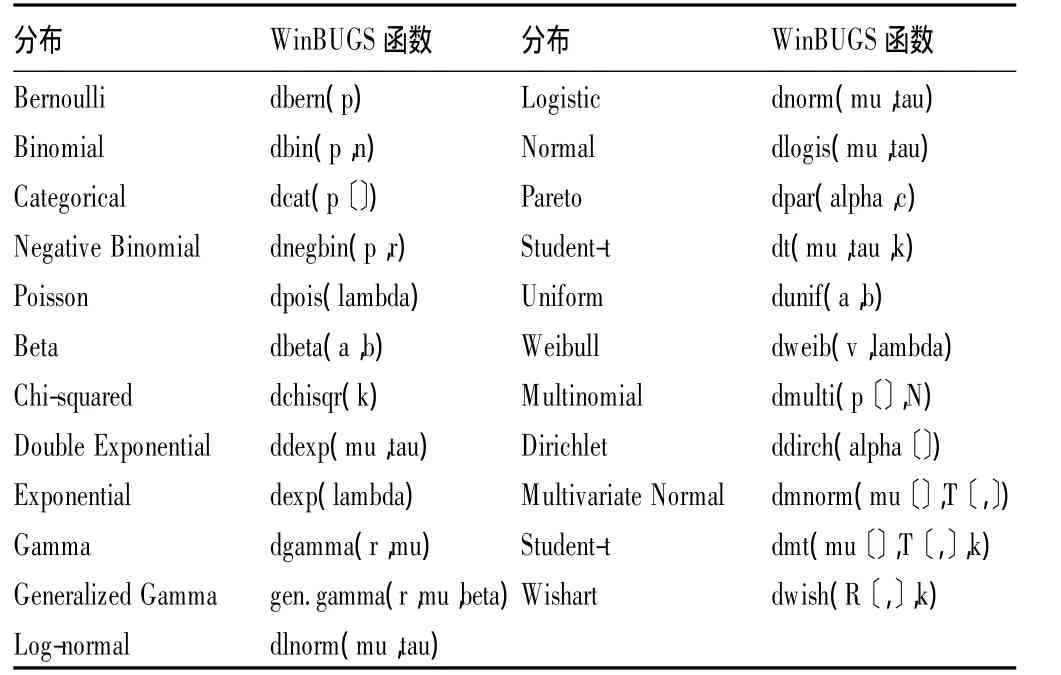
表1 WinBUGS中的常用分布

2．非标准分布的WinBUGS程序上式可看作二项分布数据yi=1，i=1，…，n的似然函数，参数pi=exp(li－c)。常数c的存在等价于右边每一项乘以因子exp(c)，显然不会影响贝叶斯后验推断，c的作用在于保证pi在［0，1］之间，可选一个大的整数，如10000。WinBUGS程序如下:

c＜-10000设定常数c，在不合适时需要调整以保证 p∈［0，1］

for i in 1:n{

l［i］＜ -＊＊＊指定对数似然

p［i］＜ -exp(l［i］-c)计算二项分布参数 p

y［i］＜-1对所有y设定为1

y［i］～ dbern(p［i］)}设定二项分布似然(2)利用Poisson分布指定非标准分布

常数c不会影响贝叶斯后验推断。上式可看作参数r=1的负二项分布数据yi=0，i=1，…，n的似然函数，参数 pi=exp(li－c)，c的作用在于保证 pi在［0，1］之间，可选一个大的整数，如10000。WinBUGS程序如下:

c＜-10000设定常数c，在不合适时需要调整以保证 p∈［0，1］

for i in 1:n{

l［i］ ＜ -＊＊＊指定对数似然

p［i］＜ -l［i］-c 指定负二项分布参数 p 为 l［i］+c

y［i］ ＜-0对所有y设定为0

y［i］ ～ dnegbin(p［i］，1)}设定负二项分布似然

实例分析

麦克德里克(McKendrick)应用数学模型研究了1906年印度孟买一个村庄流行性霍乱传染的数据〔4〕。数据显示有大约75%的家庭没有霍乱患者，有大约14%和7%的家庭有1和2个患者，患者人数超过3个的家庭数不足4%。

常数c的存在同样不会影响贝叶斯后验推断。上式可看作Poisson分布数据yi=0，i=1，…，n的似然函数，参数λi=－li+c，c的作用在于保证λi＞0，可选一个大的正整数，如10000。WinBUGS程序如下:

c＜-10000设定常数c，在不合适时需要调整以保证λ＞0

for i in 1:n{

l［i］ ＜ -＊＊＊指定对数似然

lambda［i］＜ --l［i］+c 计算 Poisson 分布参数 λ

y［i］＜-0对所有y设定为0

y［i］～dpois(lambda［i］)}设定 Poisson 分布似然

(3)利用负二项分布指定非标准分布p表示家庭中成员不可能感染霍乱的概率，I()为指示函数，当x=0取值为1否则为0。显然，ZIP的似然不能由WinBUGS软件直接指定。ZIP的对数似然函数为

表2 1906年印度孟买村庄霍乱传染数据的频数分布

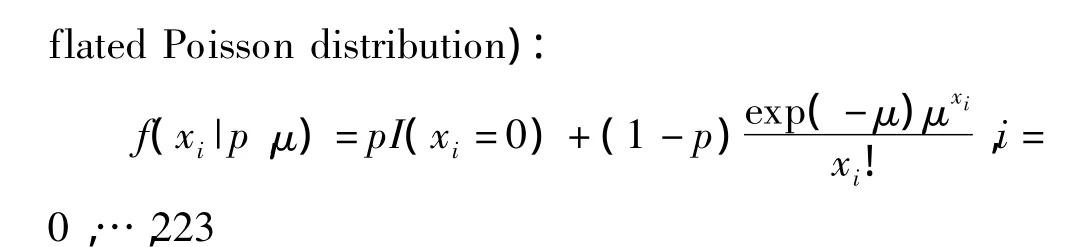
l［i］＜ -log(p*equals(x［i］，0)+(1-p)*exp(-mu)*pow(mu，x［i］)/exp(logfact(x［i］)))用ZIP的对数似然函数l［i］即可。WinBUGS函数equals(x，y)表示在 x=y时取值为1，否则为 0，pow(x，y)=xy，logfact(x)=log(x!)。Gibbs模拟总共抽样15 000例，其中前5 000例作为 burn-in样本抛弃不用〔6－7〕，则后验样本量为 10 000。p和 μ 的初始值分别设为0.5和1，c都指定为20。WinBUGS结果显示三种方法的后验统计量完全一样，见表3。

表3 三种似然构建方法的ZIP模型后验统计量

小 结

WinBUGS软件基于Gibbs算法能够从任意复杂的后验分布模拟抽样，极大地推广了贝叶斯的应用，在WinBUGS软件下能够实现很多复杂的贝叶斯统计模型，如分层模型。本文在原有WinBUGS统计分布基础上介绍了三种非标准分布的WinBUGS编程技巧，能够满足任意似然和先验的分布类型，但都需要根据所采用分布的参数要求提供一个合适的常数c。c的作用在于保证所选用分布的参数符合实际意义，理论上c可以选择一个相当大的数，在这种情况下一定能够满足分布的参数要求，但是在实际应用中，一个过大的c可能会导致计算机计算的浮点问题，这一点对二项和负二项分布尤其要注意，因此需要尝试选择一个满足要求的数值同时保证不出现计算问题。例如ZIP模型中，二项和负二项分布中c选择1000就会出现计算问题，但是对Poisson分布而言，只要c满足要求其大小对计算并不会带来什么实质问题，也基于这点原因，在实际应用时推荐使用Poisson分布构建任意分布的似然和先验。

1．Spiegelhalter D，Thomas A，Best N，et al．WinBUGS user manual，Version 1．4，2003．http://www．mrc-bsu．cam．ac．uk/bugs/winbugs/manual14．pdf．

2．Gelman A，Carlin JB，Stern HS，et al．Bayesian data analysis，2nd ed．London:Chapman ＆ Hall，2004．

3．Ntzoufras I．Bayesian modeling using WinBUGS．New York:John Wiley ＆Sons，2009．

4．徐利治．现代数学手册-随机数学卷．武汉:华中科技大学出版社，1999．

5．Lambert D．Zero-inflated poisson regression with an application to defects in manufacturing．Technometrics，1992(34):1-14．

6．Gelfand AE，Smith AF．Sampling-based approaches to calculating marginal densities．Journal of the American Statistical Association，1990(85):398-409．

7．SASInstitute Inc．Preliminary capabilitites for bayesian analysis in SAS/STAT software．Cary，NC，USA，2006．