基于连续性变量和二元变量的贝叶斯自适应剂量发现算法*

沈阳师范大学数学与系统科学学院统计学系(110034) 刘瑞银 李晓毅

临床试验中的阶段I/II试验主要研究如何确定最佳剂量。以前在阶段I/II试验中研究毒性或者有效性时，只用二元或三元的离散变量。现在越来越多的把生物标记(biomarker)作为有效性的替代结果，而biomarker是连续变量，于是如何把二元的毒性变量和连续的biomarker变量联合起来进行研究就成为了新的问题。

概率模型和先验

考虑受试者陆续进入并先后得到处理的临床试验。假设有 K 个剂量水平，d1，…，dK，xi表示第 i个受试者的剂量，Xi=(I(xi=d1)，I(xi=d2)，…，I(xi=dK))。Yi=(Wi，Ti)T表示第 i个病人的观测结果向量。Wi表示连续的biomarker变量，Ti表示二元的毒性变量，Ti=1表示观测到毒性，Ti=0未观察到毒性。

后验分布

其中，π(θ)是θ的联合先验分布。

在观测到每个受试者的结果后，用MCMC算法去更新未知参数的后验分布。令n表示阶段n观测到的受试者的总个数，N表示进入试验的受试者的最大个数。在阶段n，潜在变量Z(n)和参数θ(n)的满条件分布在下面1～5步骤中给出。首先从相应的先验分布中产生θ(n)的初始值，然后重复下面的步骤进行更新。

步骤1 产生潜在变量Zi，如果Ti=0，从截尾正态分布φZ/W(Zi，~μZ，i，~ρ2)I(Zi≤0)中产生Zi。否则，从φZ/W(Z，~μZ，i，~ρ2)I(Zi＞0)中产生。

步骤2 基于前n个受试者的结果产生βZ，βZ，k|Z，W，σW，ρ，βZ，－k的满条件分布为截尾的单变量正态，其均值为 ~βZ，k，标准差为 ~σZ，k，具体形式如下:

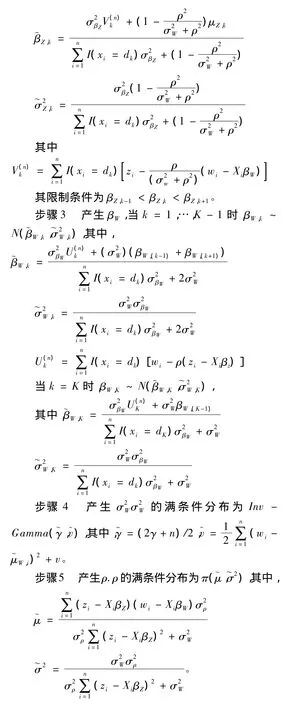
决策准则

为了确定可接受的剂量，首先必须给出具有临床意义的可接受的最小生物标记表达水平W*min和最大可耐受毒性概率πt。在试验开始，把m个受试者安排在最低剂量，1≤m≤6。nk表示dk处的受试者个数，如果nk≥m，则认为dk被充分试验了。令δ1，δ2，δ3为提前

模拟研究

为了评价所提算法的操作性质，本文进行了模拟研究。对于 s情形下的第 k个剂量，s=1，…，4，k=1，…，4，记相应的毒性概率为 ps，k，标准化的平均生物表达水平W定义为平均表达水平除以W*max。最大可接受毒性概率πt设为35%，最小生物表达水平为5%。

产生相关系数为0.25的标准二元正态随机变量(z1，z2)，令(u1，u2)=(Φ(z1)，Φ(z2))。在情形s中的第 k个剂量下，如果u1≤ps，k，则受试者中毒，u1＞ ps，k，不中毒;令 G－1(·| τλs，k，τ)表示均值为 λs，k的伽玛分布的逆分布函数，w=G－1(u2|τλs，k，τ)则为生物标记表达结果，其中，τ=0.10。参数的先验分布如下确定:βZ，k的先验位置参数 μZ，1，…，μZ，K设为 0，1.9，－ 1，－7.5，σβZ设为4，βW，0=5，σβW=1000，ρ和σW用模糊先验。

在MCMC模拟中，迭代10000次，前5000次为预热，在后5000次迭代中每5个迭代取一个值，共进行了1000次模拟，其中受试者数目最大为36。在情形1中，在3个可接受的剂量(1，2，3)中推荐了第3个剂量，因为剂量4毒性太大，剂量1和2的生物表达水平又比剂量3低。利用提出的模型和决策准则，算法以95%的概率选择了剂量3。在情形2中，由于高的中毒率所有4个剂量都是不可接受的;算法以94%的概率没有选择任何一个剂量，大部分试验都以平均样本量15早早终止，且受试者几乎都被安排在第1剂量。在情形3中，只有剂量1的毒性是可以接受的，在试验中它以94%的概率被选中。在情形4中，所有的剂量都是无效无毒的，99%的试验不选择任何剂量，而且以平均14个病人数早早结束试验。与情形2受试者都被安排在较低的剂量不同，在情形4中，受试者均匀的分布在所有的剂量中。基于所给出的算法，一旦较低剂量显示出是安全的，接下来将在较高的剂量处作试验。如果所有的剂量都被试验了且没有发现活动性，试验则停止。

结 论

在临床试验中当同时获得毒性和连续活动性结果时，本文介绍了一种新类型的剂量发现试验，即基于一个连续性变量和二元毒性变量的贝叶斯自适应剂量发现算法。这个算法具有以下特点:(1)利用了状态空间模型。在药物发展的早期阶段，人们倾向于用一个灵活的模型去描述活动性结果和剂量之间的关系。状态空间模型使得我们可以借助剂量的力量，而不需要严格的模型假设和剂量与生物活动性之间的非线性关系。(2)根据临床经验确定超参数的值。确定超参数时需要遵循以下原则:先验参数的值应该反映了医生的信念;先验参数不能主导观测数据。为了确保先验是合适的，建议在进行试验之前通过模拟研究检查一下算法的操作性质。(3)概率定位改善了设计的整体操作性质。本设计并不把受试者安排在推荐得分最高的剂量处，而是在可接受剂量中以推荐得分算出的概率随机安排受试者，比较高的推荐得分意味着以比较高的概率安排受试者到此剂量。

1．Bekele BN，Shen Y．A Bayesian Approach to Jointly Modeling Toxicity and Biomarker Expression in a Phase I/II Dose-Finding Trial．Biometrics，2005，61(2):343-354．

2．刘沛，羊海涛，强来英，等．贝叶斯统计在高准确度筛检试剂评价中的应用．中国卫生统计，2010 27(4):348-350．

3．尉洁，宋娇娇，赵晋芳，等．基于贝叶斯估计的诊断试验ROC曲线回归模型．中国卫生统计，2010，27(2):152-154．

4．Liu RY，Tao J，Shi NZ．An Optimal Phase I/II Design Utilizing Severe Toxic and Moderate Toxic Response Information Separately．Wseas transactions on biology and biomedicine，2006，3(7):553-559．

5．茆诗松，王静龙，濮晓龙，编著．高等数理统计．北京:高等教育出版社，1998．