基于潜变量Gibbs抽样的Probit回归*

徐州医学院流行病与卫生统计教研室(221002) 王 婷 曾 平 何 鹏

Probit回归最先由Bliss在1934年提出〔1〕，在进行杀虫剂的毒理实验时，Bliss发现了一个有趣的现象:无论他配制的杀虫剂浓度有多高，在用药之后总会有一两只昆虫还活着;无论他怎么稀释杀虫剂，即便只是用装过杀虫剂的容器，试验结果也总会有几只昆虫死掉。Bliss原创性地采用概率分布这种新的数学思想来解决杀虫剂实验时所遭遇的困境。Probit回归建立了“剂量”与“使用该剂量时一只动物会死掉的概率”这两者间的关系，因此称为Probit(单位概率)模型，现在已经越来越多地应用到二分类数据的回归分析中。本文将主要在贝叶斯统计框架内讨论Probit回归和参数后验分布的潜变量Gibbs抽样。

方法和原理

1．Probit回归和后验分布

设解释变量为X，回归系数向量为β，根据广义线性模型原理〔2〕，可建立 Probit回归:

这里假定事件发生服从参数为p的Bernoulli分布，n表示样本量，Φ表示标准正态的累积概率分布函数，如Φ(1.96)=0.975，Φ－1为累积分布函数的逆函数，如Φ－1(0.975)=1.96，这样通过Probit连接函数Φ－1将取值为0～1之间的p映射到了整个实数空间。似然。设 g(β)为回归参数β的先验分布(prior distribution)，贝叶斯统计和频率统计最大的区别之一就在于假定参数为随机变量，当有关于未知参数的历史知识、主观认识或者专家意见时，可以选择有信息先验。当对未知参数的信息一无所知、或先验分布有太多参数需要指定时，认为参数在其空间内有等可能的取值概率而不特别偏向某些取值，则选取均匀分布作为先验分布，又称贝叶斯假定。根 据 贝 叶 斯 原 理， 后 验 分 布〔3〕(posterior distribution)p(β|Y，X)为:

3．潜变量Probit回归的Gibbs抽样

设存在一个潜在的连续变量 y*，y*称为特征(trait)或倾向得分(propensity score)〔5〕。考虑以下的模型:均数(－1.5897)和中位数(－1.5018)来看，男孩比女 孩更易发胖。

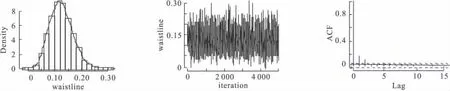
图1 腰围后验样本的直方图、核密度图、轨迹图和自相关图

表1 参数的后验样本描述

讨 论

本文讨论了医学领域中二分类数据分析的贝叶斯Probit回归，像绝大部分贝叶斯模型一样，贝叶斯Probit回归参数的后验分布异常复杂，需要采用MCMC模拟抽样，Gibbs抽样是众多MCMC算法中最常用的模拟方法。Gibbs抽样中需要已知参数的满条件分布，在此基础上迭代抽样生成参数的Markov链，但从Probit回归的后验分布却不能得到简单并且抽样方便的满条件分布，因此执行Gibbs抽样也就不大可行，本文通过增加潜在变量解决了这个问题。

潜在变量并不能被观察到，因此在贝叶斯统计中当作未知量看待，则此时Probit回归的后验分布为g(β，Y*|Y)，是回归参数和潜变量的联合密度函数。在这个后验分布中，β，Y*各自的满条件分布分别是g(β|Y*，Y)和 g(Y*|β，Y)，在 Probit回归中，前者为多元正态分布，后者为截尾正态分布，这两个满条件分布都比较简单而且容易直接进行模拟抽样，因此执行Gibbs抽样也就没有困难。在给定回归参数初始值后在这两个满条件分布之间反复迭代生成参数和潜变量的Markov链，在算法收敛后则可认为生成的参数序列来自Probit回归后验分布。构造潜变量的Gibbs抽样可以看作是一种数据扩增技术，通过在模型的后验分布中增加辅助变量使得Gibbs抽样更加容易。另一个好处是，生成的潜在变量向量可以进一步作为模型诊断的信息加以利用。

1．Salsburg D．The lady tasting tea:how statistics revolutionized science in the twentieth century．Holt Paperbacks，2002．

2．Dobson AJ，Barnett A．An introduction to generalized linear models，third edition．Chapman ＆ Hall，2009．

3．Gelman A，Carlin JB，Stern HS，et al．Bayesian data analysis，2nd ed．London:Chapman ＆ Hall，2004．

4．Albert J．Bayesian computation with R，2nd Ed．New York:Springer，2009．

5．Lynch SM．Introduction to applied bayesian．Statistics and Estimation for Social Scientists，New York:Springer，2009．

6．http://www．r-project．org/