基于多状态Markov模型的老年人认知损害转归研究*

杨珊珊 李新毅 周立业 梁瑞峰 罗天娥 曲成毅 余红梅△

阿尔茨海默病(Alzheimer's disease，AD)是老年期痴呆的一个主要类型。目前一般认为轻度认知损害(mild cognitive impairment，MCI)是一个有轻度认知缺损但没有痴呆的疾病分类单元，是介于正常老化和痴呆之间的一种中间过渡状态;而AD的发生和发展将呈现进行性加重和不可逆性特点。

以往的MCI转归研究多采用经典的统计学方法，如logistic回归、Cox回归等，这些方法不能同时分析疾病各发展阶段的影响因素和动态评价转归。多状态Markov模型作为处理随访资料的有效工具，可同时考虑所有的状态、结局、状态间转移的时间信息以及可能的影响因素，对随机过程进行连续性动态研究，动态地评价疾病进展，是目前为止研究疾病不同转归的最佳模型〔1〕。本文将多状态Markov模型应用于MCI转归研究，分析MCI患者不同认知状态变化的影响因素及其转归规律，为今后类似研究提供方法学借鉴，拓宽多状态Markov模型在医学领域的应用范围。

资料来源

采用分层整群随机抽样方法，调查太原市65岁以上社区老年人6 192人，其中认知正常老化者5 592人，MCI患者600人。之后每6个月对这600名MCI患者进行一次随访，每次随访内容包括社会人口学指标、生活方式、健康状况及认知水平等〔2〕。至2009年4月已完成4次随访，期间因死亡、搬迁、外出、拒绝参加观察等原因失访人数72，失访率12%。600例MCI患者中，男性174例，女性426例，年龄范围为65～90岁，平均年龄为(69.71±6.59)岁。

原理与方法

1. 基本概念〔1，3〕

(1)暂态(transient state):指从此状态可发生状态的改变，转移到其他状态。

(2)吸收态(absorbing state):指从其他状态转移到此状态后，不能再发生状态的转移。

(3)转移强度(transition intensity):描述状态间的瞬时转移危险，即在t时刻前处于状态i的个体，将在很短的时间区间内转移到状态j的概率。

(4)转移概率(transition probability):给出在时刻s处在状态i的个体，将在后来的时刻t处在状态j的可能性。

(5)逗留时间(sojourn time):指病人处于某状态的时间长短。

(6)马尔可夫(Markov)性:又称“无后效性”，指从现状态转移到下一状态仅仅取决于目前状态，而与过去的各状态无关。

(7)状态结构(state structure):明确状态及哪些状态间的转移是可能的。

2.多状态Markov模型

(1)模型简介

Markov过程是以俄国数学家Markov AA命名的一种非参数离散型时间序列分析方法，主要用以模拟随时间发生的具有Markov性的随机事件。多状态Markov模型建立之初，被用来描述和预测煤气的分子在一个密闭容器中的状态〔4〕。随后在近代物理、生物学、管理科学、信息处理与数字计算方法等方面都有重要应用，最早应用于医学领域是在20世纪70年代，主要用于模拟慢性疾病的发展过程，20世纪80年代后国外已有大量的应用。截至目前，多状态Markov模型是探讨慢性病不同发展阶段影响因素及转归规律较有效的统计方法。

齐次Markov过程假定所有转移危险在时间上是恒定的，即状态间的转移强度是常量。由于齐次Markov模型的转移强度恒定，转移概率是转移强度的显式函数，参数估计与统计推断相对比较容易，应用比较广泛。

(2)参数估计和假设检验

设有N个个体，mi为第i个个体参加观察的次数，在tj和tj+1观察时刻所处的疾病状态分别为r和s，qrs为转移强度矩阵中的元素;q(0)rs表示状态r转移到状态s的基线转移强度;z(t)表示状态r转移到状态s这个阶段所对应的协变量向量;βrs表示协变量所对应的回归系数。则多状态Markov模型可表示为:

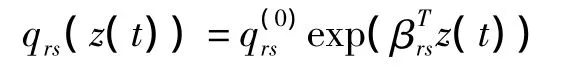
某次观察对似然函数的贡献为:

则整个似然函数为每个个体每次观察对似然函数贡献的乘积，即

采用Quasi-Newton迭代法可获得模型参数的极大似然估计值，同时通过构造信息矩阵可获得这些参数标准误的渐近估计值〔5〕。

结 果

1.多状态Markov模型的构建

假定MCI进程中，从现状态转移到下一状态仅仅取决于目前状态，而不直接受以前各状态的影响，即具有Markov的“无后效性”特征，因此选用多状态Markov模型描述MCI转归规律。本文通过智商(intelligence quotient，IQ)变化反映MCI认知功能的变化趋势，结合MCI的转归存在异质性，MCI大部分发展为AD，小部分稳定或好转。特确定一个四状态模型，即:状态1(认知稳定):与基线智商相比较，变动范围不超过±1倍标准差;状态2(认知轻度恶化):与基线智商相比较，降低高于1倍标准差，但小于2倍标准差;状态3(认知好转):与基线智商相比较，升高大于1倍标准差;状态4(认知重度恶化):与基线智商相比较，降低高于2倍标准差。

假设MCI转归中，相邻状态间可以相互转化，但认知好转和恶化之间不能相互转化，认知功能发展成为重度恶化后将不再可逆，即将状态1～3作为暂态，状态4作为吸收态。由此构造的多状态结构图见图1。

根据转移强度矩阵各行之和等于0，及对角线的转移强度等于该行中其他转移强度之和的相反数，该模型的转移强度矩阵Q如下，共有6个待估转移强度:q12、q13、q14、q21、q24和 q31。

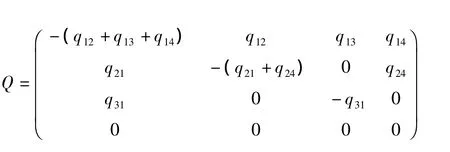
图1 MCI患者认知变化状态结构图

2.多状态Markov模型的拟合结果

采用R软件中的msm package进行多状态Markov模型分析〔6〕。依据各观察时刻所处的状态，得出各状态相互转移出现的频数，见表1。

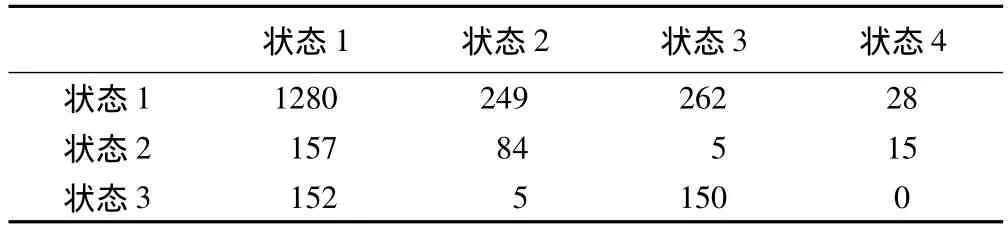
表1 各状态转移频数

根据各状态相互转移频数，经过多次迭代计算，最后设定初始转移强度矩阵为:

(1)影响因素、转移强度和转移概率

多因素分析结果、转移强度和转移概率估计见文献〔2〕。

(2)逗留时间

本文计算了从基线到追踪观察2年各状态总逗留时间。平均而言，每个MCI病人认知功能稳定时间大约为6.4年，处于轻度恶化的时间约为3.6年，好转时间约为5.2年。

(3)转归预测

将吸收态(状态4)作为生存分析的终点，状态1、状态2和状态3分别作为起点，可得到三条生存曲线，图2和图3分别为2年和5年内所对应生存曲线。其横轴为时间，纵轴为期望生存率(expected probability of survival)。

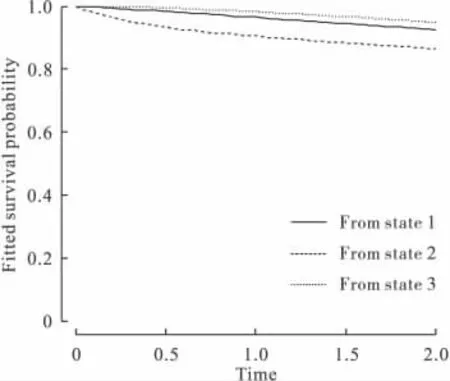
图2 生存曲线(2年)

(4)拟合优度评价

图3 生存曲线(5年)

图4分别给出了每个状态实际频数和理论频数百分比曲线，其横轴为时间，纵轴为实际频数百分比和理论频数百分比，通过观察两条曲线的吻合程度，我们可以对多状态模型拟合优度进行初步评价。本文有5次观察时间资料，时间间隔是6个月，模型拟合开始部分较差，之后趋于重叠，模型拟合较好。

图4 模型评价图

讨 论

1.多状态Markov模型的特点

生存分析己在医学研究中得到广泛应用，传统的生存分析可称为两状态模型(two state model)，因为只可观察到两个状态和一个时间间隔。因此，它属于单过程的生存分析。许多疾病，尤其是慢性病的发展通常具有多阶段、多状态的特点，这些阶段或者状态可以依照一定的专业知识划分，从而可以分析影响疾病转归的因素在不同阶段的作用强度或方式，为疾病防治提供理论依据。本文以MCI转归为例，说明了多状态模型的应用，基本方法同样可以用来分析其他慢性病、肿瘤以及其他具有阶段性变化的疾病进程。

多状态Markov模型种类繁多，在实际应用中，应根据专业依据选择模型种类和转移模式。在此基础上尽量使模型简约，如规定不能进行逆转，各状态只能渐进，则处理起来就比较方便。如在癌症和某些严重的慢性病治疗或随访观察过程中，其病情逐渐加重、产生并发症并最终导致死亡。据此可以进行模型简化。

尽管多状态Markov模型在分析随访资料时具有许多优点，但也有一些局限性。首先Markov模型建立在一定假定条件之上，它假定疾病的发展仅仅取决于目前状态，而与过去的各状态无关。在临床实际中，疾病的转归可能还会与一些重要的既往史有关，所以我们应根据临床意义合理选择多状态的类型。其次，由于状态划分和建模的多样性，实际工作中者很难编制相应的计算程序，这在一定程度上限制了其推广使用。理论方面还存在一些问题，如拟合优度检验，左删失、右删失及区间删失均存在情况下的参数估计〔7〕。

2.多状态Markov模型应用注意事项

(1)模型中的状态必须能够代表疾病进展过程中的典型阶段或重要事件，这些状态间必须互不相容，以确保模型中患者在任何时点只处于一种状态。可以有一个吸收态，也可以有一个以上的吸收态，在慢性病研究中一般将“死亡”作为吸收态，也可以根据吸收态的不可逆性，将病情比较严重、几乎不可逆转的某种状态作为吸收态。在多状态Markov模型中，状态的多少、状态之间是否可逆、哪种状态作为吸收态，随研究目的不同而不同，应根据专业知识确定转移模式。

(2)Markov模型在较长时间后，逐渐趋向稳定，而与初始状态无关。尤其是进行预测时，要求观察的时间序列要足够长。

(3)应尽量有准确的观察开始时间、进入吸收态的时间或删失时间，每个个体发生任何一次转移的时间。若限于人、财、物等客观条件，只能定期对病人进行检查，如每年1次，两个相邻的状态时间点之间处于什么状态判断不清楚，即著名的时间间隔疏漏(time interval omission)问题〔8〕。

1．Andersen PK，Perme MP．Inference for outcome probabilities in multistate models．Lifetime Data Analysis，2008，14:405-431．

2．杨珊珊，周立业，梁瑞峰，等．多状态Markov模型在社区老年人轻度认知损害转归分析中的应用．中华流行病学杂志，2011，32(1):25-28．

3．余红梅．多状态模型简介．中国卫生统计，2005，22(3):177-180．

4．易华云，刘爱忠，张琰．Markov模型在卫生领域中应用简介．循证医学，2008，8(3):172-176．

5．Meira-Machado L，U~na-Álvarez J，Cadarso-Suárez C，et al．Multi-state models for the analysis of time-to-event data．Statistical Methods in Medical Research，2009，18:195-222．

6．Jackson C．Multi-state modeling with R:the msm package(version 0．9．1)，2009．

7．傅承主，方积乾，柳青．疾病自然史的随机模型．生物数学学报，1996，22(5):133-138．

8．安小妹，凌莉．Markov模型在生命统计中的研究进展．中国卫生统计，2007，24(4):436-439．