破损舰船最小初稳性高计算方法研究
2012-03-09胡丽芬纪卓尚郑红霞倪秀英
胡丽芬 马 坤 纪卓尚 郑红霞 倪秀英
(鲁东大学交通学院1) 烟台 250064) (大连理工大学船舶CAD工程中心2) 大连 116024)
0 引 言
初稳性是舰船稳性的一项重要指标,舰船破损后多舱进水,一方面如果第二类积水舱大量存在,产生大面积的自由液面,需要对计算得到的初稳性高进行自由液面修正;另一方面由于存在第三类淹水舱,水线面损失严重,有效水线面面积减少,稳性大大降低,如果舰船的最小初稳性高很小或近似为负值,则舰船处于危险状态.自由液面对初稳性高的修正按照规范[1]进行计算即可,主要是计算破损后未修正前的最小初稳性高h.对于完整船通常横初稳性高hθ就是h,初稳性好坏用横初稳性高来度量.对于破损船,通常认为平衡浮态时的有效水线面及其水下要素计算复杂,为了计算方便目前也多数采用h在中站面上的投影,即hθ来表达破损后的初稳性.但此时,破损后hθ不是h,对于初稳性高很小或接近0时会带来初稳性高正或负的错误判断.特别是在抗沉辅助决策时,初稳性高为正和为负时的抗沉措施有着本质的区别,决策不当反而会使舰船产生更大倾斜,甚至于倾覆,因此有必要计算破损后的h.
对于船舶完整和破损后初稳性的研究,许多学者进行了有益的探索[2-4],但是有关舰船h方面的研究在国内外还未见有正式报道.本文基于舰船静力学的基本原理,探讨了h的计算方法,并按照该方法实现了破损后的h计算,为紧急情况下正确决策奠定基础.
1 最小初稳性高计算原理
文中按损失浮力法计算破损后的h,破损前后重心位置不变,关键是浮心位置和稳心半径的求解.舰船破损后的浮态计算采用非线性规划法求解平衡方程[5].由于平衡方程是非线性隐式表达,采用逐次线性化方法进行迭代计算.为计算初稳性高的最小值,关键是要计算破损后的倾斜水线面对通过其形心的最小惯性矩,然后按照式(4)~(6)进行计算.
1.1 有效水线面最小惯性矩计算
舰船破损后,水线面有效面积发生了变化,主惯性轴也发生了改变,不但会平移,不对称进水时还会发生转动.
如图1所示,ξoη为完整时的船体坐标系,ξF和ηF分别为破损后通过有效水线面漂心且平行于船体坐标系的坐标轴.l为主惯性短轴(面积对其惯性矩最小),L为主惯性长轴(面积对其惯性矩最大),ε为FξF与Fl之间的夹角,由FξF正向算起,以逆时针方向为正.其中,
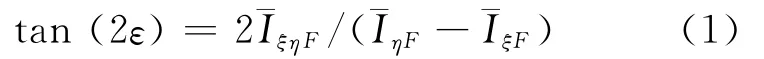
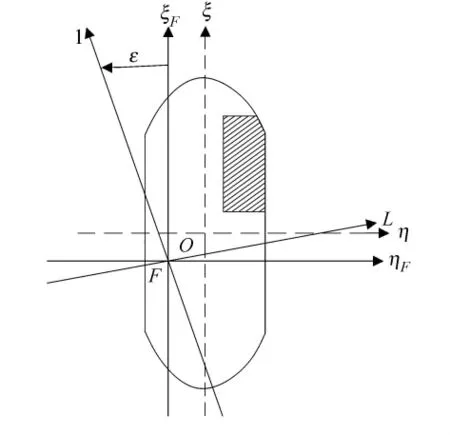
图1 破损舰船倾斜水线面主惯性轴
在这种情况下,舰船的横倾和纵倾实际上是绕l,L轴进行,即在垂直于主惯性轴l和L的平面(主倾斜平面)内发生,则实际的最小惯性矩¯Il和最大惯性矩¯IL,按照平面图形的几何性质求解的相关知识,可写成如下形式:
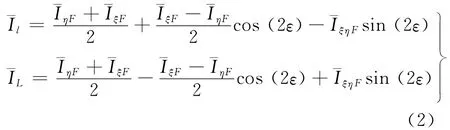

式中:IξS为船体完整水线面对中心轴ξ的惯性矩;iξp为进水舱损失水线面对中心轴ξ的惯性矩;IηS为船体完整水线面对η轴的惯性矩;iηp为进水舱损失水线面对η轴的惯性矩.
1.2 最小初稳性高h计算
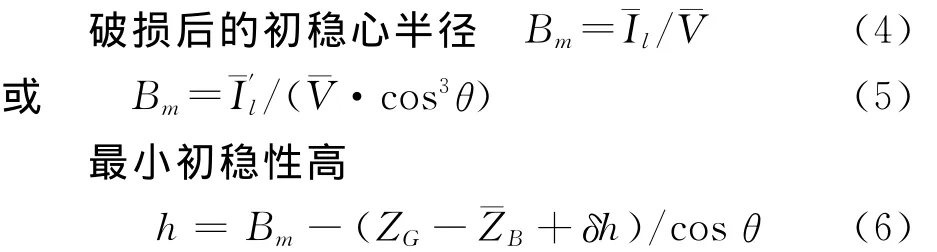
其中,排水体积及其形心坐标利用梯形法按纵向积分进行计算,关键是先计算出任意水线下各横剖面的面积和面积矩.而水线面面积各要素是要计算任意水线处水线面的面积、面积矩和惯性矩.这两者都可归结为平面几何图形的面积要素计算.本文采用封闭曲线积分法计算[6].
2 实例分析
为了比较h和hθ之间的差别大小,以某船为例.假定破损状态为尾部右舷破损,分别计算得到4.2m水线下完整和最终平衡位置时的水线面要素如表1所列.初稳性高的结果如表2所列.
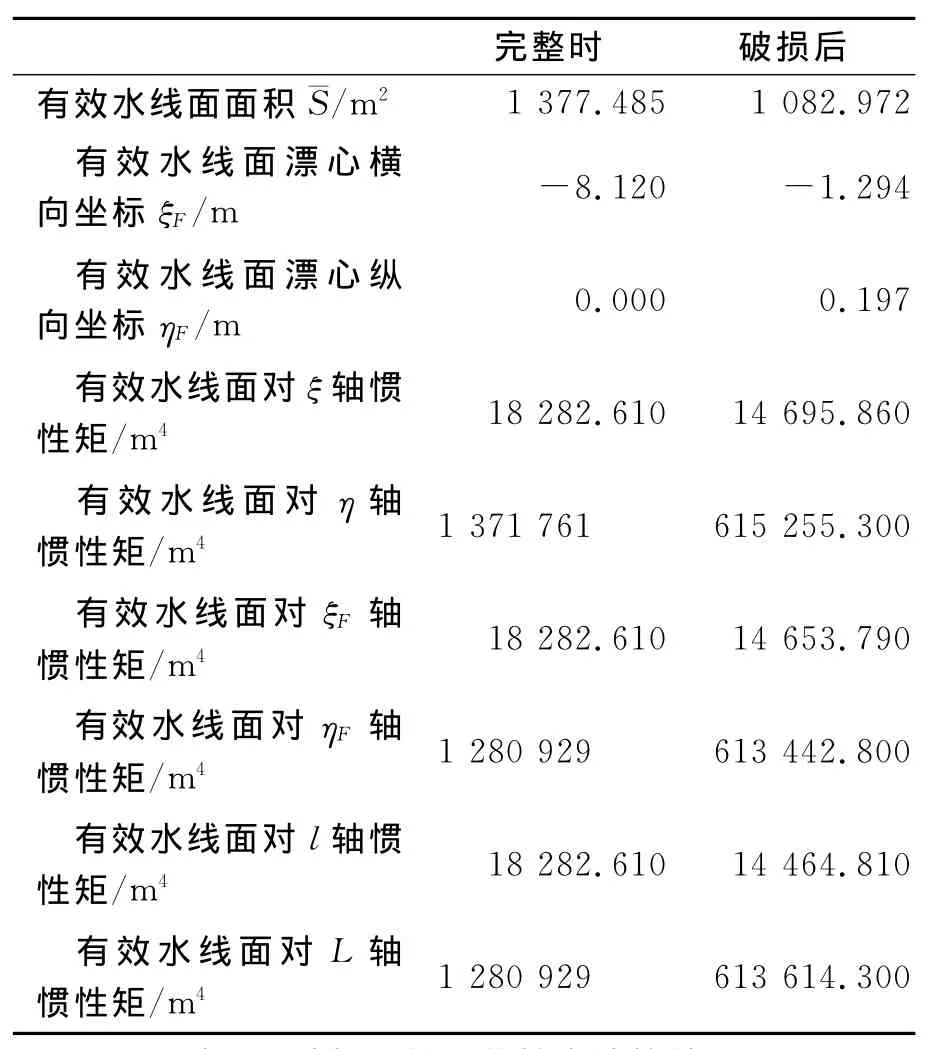
表1 完整和破损后的水线面要素
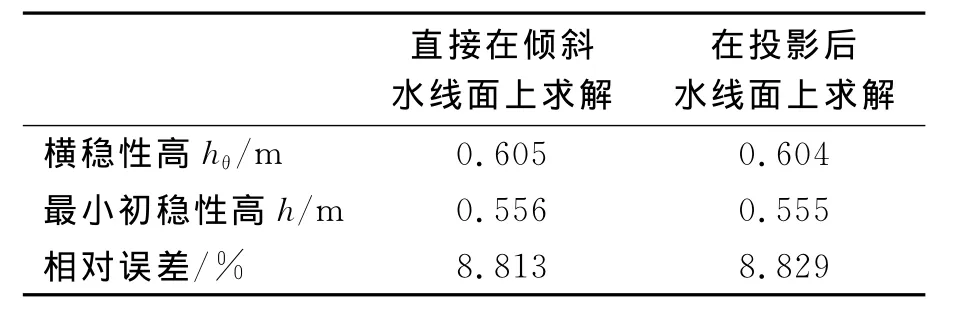
表2 破损后的初稳性高计算结果
表2分别为在倾斜水线面上求出的h和hθ;并和在投影后的水线面上求出的各要素进行了对比.从结果可以看出,2种方法求得的初稳性高差别很小,因此可以用投影后水线面上的结果来近似.
由表2可见,不论采用哪种方法(直接在倾斜水线面上和在投影后的水线面上求解),h和hθ的结果差别较大,采用hθ来代替h的方法偏于危险,尤其在舰船破损后水线面损失严重的情况下.同时,求解h并没有比hθ耗费多余的计算时间,因此为了保证计算精度,有必要计算破损后的最小初稳性高h.
3 结 论
1)本文采用损失浮力法计算舰船破损后的最小初稳性高h.通过直接在倾斜水线面上计算,和其在基平面上投影后水线面的有效要素计算的两种方法的实例分析,表明两种方法的计算结果差别很小,可以用投影后水线面上的计算结果来近似,简化了计算过程.
2)通过h和hθ的计算结果比较,证实了h的计算值能更好的反映舰船破损后的稳性情况.
3)与hθ的计算相比,求解h没有耗费多余的计算时间.因此舰船h的计算对于水线面损失严重的破损情况尤其需要,这为紧急情况下辅助决策参考提供重要依据.
[1]解放军总装备部军标出版发行部.GJB 4000-2000舰船通用规范[S].北京:总装备部军标出版发行部,2000.
[2]魏建志,程智斌.舰船产生负初稳度时的稳性研究[J].海军工程大学学报,2001(6):90-94.
[3]马 坤,张明霞,纪卓尚,等.非线性规划法计算船舶稳性[J].中国造船,2003,44(2):81-83.
[4]马 坤,李作志,杨 洋.舰船完整稳性实时计算方法研究[J].大连理工大学学报,2007,47(3):383-386.
[5]马 坤,张明霞,纪卓尚.基于非线性规划法的船舶浮态计算[J].大连理工大学学报,2003,43(3):329-331.
[6]林 焰,李铁骊,纪卓尚.破损船舶自由浮态计算[J].大连理工大学学报,2001,41(1):85-89.
