利用单传声器分解和测量管道内高次模式声波
2012-03-07冯善勇莫方朔赵跃英盛胜我
冯善勇,莫方朔,赵跃英,盛胜我
(同济大学声学研究所,上海200092)
当声波在管道内传播时,除了对应零次模式的平面波之外,通常还存在高次模式的声波.研究模式分解技术以及精确测量高次波的强度,对于分析管道中声波的产生和传播是非常重要的.模式分解技术目前主要是以解析的方式将管道中的声场按各阶模式展开,然后通过管道中的多点测量加以求解,从而得到各次模式的强度.1972年,Moore[1]最早提出了一种在圆形管道中的高次模式分解方法,声源采用周期性信号,利用两个传声器获得信号.但此方法只考虑了圆周向模式,而未考虑径向模式,且无法分离每个模式的入射和反射分量.1981年,Kerschen等[2]提出了在圆形管道中应用于周期信号和随机信号的模式分解法.但此方法同样不能分离反射波分量,并且只考虑了圆周向的模式分解.1987年,Salikuddin等[3-4]提出了使用瞬态信号进行测量的模式分解法.在这一系列工作的基础上,1989年,Abom[5]基于测量一对传声器之间的传递函数,提出了可以适用于任何类型声源信号的模式分解法,并能测量入射和反射部分能量.1998年,Akoum等[6]同样基于双传声器传递函数法,对圆形管道中的高次传播模式进行分解.试验中使用的声源信号为白噪声,通过旋转声源和改变两个传声器的径向位置形成多种不同的测量条件,分别测得两传声器之间的传递函数,进而由这多个传递函数对管道中的模式进行分解.2006年,Sitel等[7]利用四个传声器组成的接收系统对圆形管道中的高次模式进行分解.Schultz等[8]利用传声器阵列得到了管道内传播的高次模式声波.与以前的工作相比,此方法不需要测量两个传声器之间的传递函数,而是通过大量传声器同时测量的数据直接进行模式分解.介绍了包含八个传声器的阵列,分解出在方形管道中存在的前4次传播模式.2009年,Lau等[9]为了测量T字形方管中高次模式的传播特性,安置了16个传声器,分解管道中存在的前4次传播模式.但是,由于这种方法所分解的高次模式数量受到传声器数量的限制,传声器增多时,会对管道中的原始声场产生干扰,同时存在传声器匹配等问题.
本文提出通过单传声器代替传声器阵列对管道高次模式声波进行测量的方法.采用单传声器在管道内沿轴向均匀传动获得声压信号,运用模式分解的方法,得到管道中各个传播模式声波的强度.这种方法克服了传声器阵列测量时对声场的干扰,也避免了传声器之间的匹配问题.同时,对管道内所能分解的高次模式数量,在原则上并没有限制.
1 管道内高次模式声波的分解
如图1所示,在直角坐标x,y,z中,设z轴为沿管轴的声传播方向,x轴和y轴与管道横截面内的管壁方向平行.由于壁面边界条件对声传播的约束,管道内的声场是沿z轴正方向和反方向传播的所有模式声波的叠加.
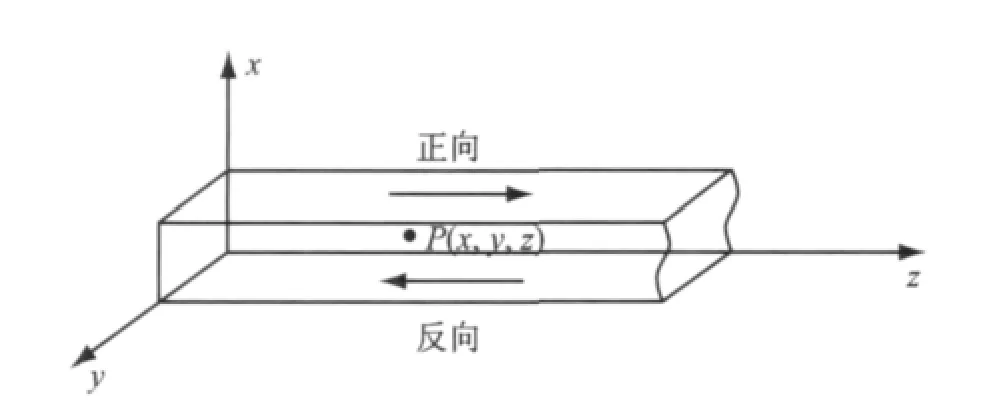
图1 声波在管道内传播示意图Fig.1 Schematic diagram of sound propagation in ducts
管内任意点的声压P(x,y,z)可写为
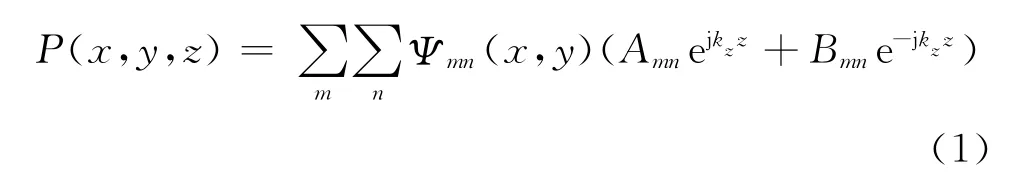
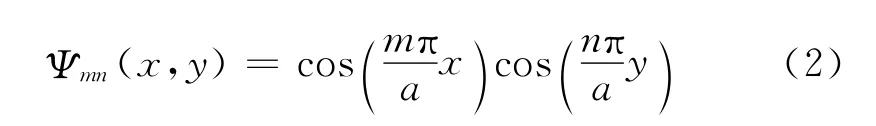
式中:a为管道的边长.轴向的波数kz相应为
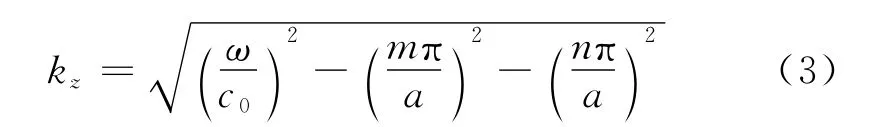
式中:k=ω/c0为波数,ω为角频率,c0为声传播速度.
如果声压P(x,y,z)的值能够通过实测得到,则管内传播的正向波与反向波的振幅Amn,Bmn都可以由式(1)求得.假设管道中存在的所有稳态传播模式数为N,则式(1)中包含2 N个未知系数.因此,最少需要2 N个传声器测点才能得到各模式的幅值.设测点数为M,且M≥2 N,应用所有测点的声压值,可以形成一方程组

式中:P1,P2,…,PM对应各测点的声压.为了得到所有模式,传声器测点应离散地分布在横截面和轴向上.方程组(4)可以用矩阵的形式简洁地表达为

式中:P表示所测点处的复数声压,为M×1的向量;L是由式(4)给出的M×2 N的系数矩阵,包括横截面函数和复指数的传播函数;G表示各个模式的复数振幅,为2 N×1的向量,它可以进一步表示为

由上述可知,若要对管道中包含N个传播模式的声场进行分解,至少需要在管道中放置2 N个传声器进行同时测量,才能将各个模式的幅值求解出来.对于测点数M大于2 N的超定方程情况,可以通过最小二乘法进行求解[10].
2 单传声器分解与测量高次模式声波
目前分解管道内高次声波传播模式的方法一般都是通过安装在管道内的多个传声器同时测量.但是,这种方法不但需要复杂的传声器阵列装置,而且还存在两个主要缺陷.首先,传声器的数量随着待分解模式数的增加而增加,而大量的传声器会对管道中的原始声场产生严重干扰.其次,传声器之间存在匹配的问题,增加了试验的复杂程度,也影响了试验的精度.
利用目前的数字声源信号可完全重复的特点,本文提出了沿管道轴向均匀传动的单传声器测量系统.在管道的一端发射声信号,精确地控制单个无指向性传声器在管道中均匀传动,使其在一系列测量位置上获取稳定的声压信号.由于数字声源信号的完全可重复性,这一组声压信号等效于由一个线形传声器阵列所获得.
发声系统采用扬声器激发,由计算机生成的数字化信号驱动.记信号的重复周期为T,每个周期由一段有效的激励信号和一段静音组成,激励信号可采用纯音或者扫频信号.根据实际声场情况,适当选择激励信号和静音的长度,以保证在不同周期内管道中的声场完全相同,而且相邻周期内不会相互混迭.
接收系统采用单个无指向性传声器,由步进电机控制其在管道内沿轴向均匀传动.步进的周期也为T,其中包含传声器在两个相邻测点间匀速移动的时间,以及传声器在单个测点上滞留的时间.
将声源系统和接收系统进行同步控制,以保证传声器在每个测点位置滞留的时间内,声源刚好激发有效的声信号.假设在整个测量过程中,传声器测得的声信号为p(t),将其进行连续性分段处理
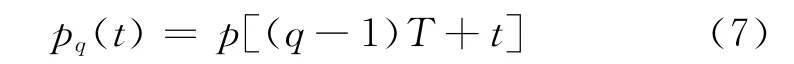
式中:q=1,2,…,M,且0<t≤T,即可以得到M个持续时间为T的声压信号pq(t),所得的结果等效于沿管道均匀分布的M个传声器组成的线形阵列实时测量所接收的信号.通过数据处理后,可得到各测点处与空间相关的复数声压Pq.在图1所示的情况下,传声器沿z轴方向直线步进,设步进间隔为d,代入式(1)中,则有
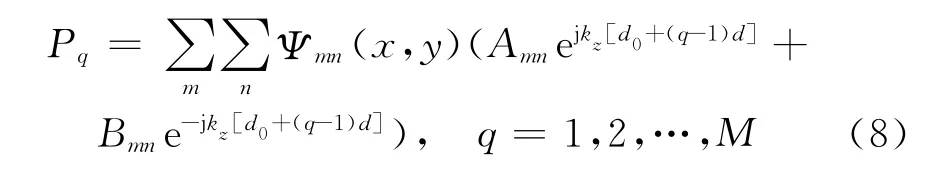
式中:d0为第一个测点在z轴上的坐标值.
进而应用式(1)~(6)中所述的模式分解法,只要满足M≥2 N,就可求得管道中存在的各传播模式的振幅.
实现单个传声器分解与测量高次模式声波的基础主要有两点:一是数字声源信号可完全重复;二是配合控制传声器精确地传动.当传声器滞留在每个步进位置上时,保证管道中的声场完全一致,从而达到以单传声器一次测量代替多传声器同时测量的效果.
3 试验结果
3.1 装置
为了验证本文所提出的单传声器高次模式分解测量系统的有效性,建造一个如图2所示的测量装置.
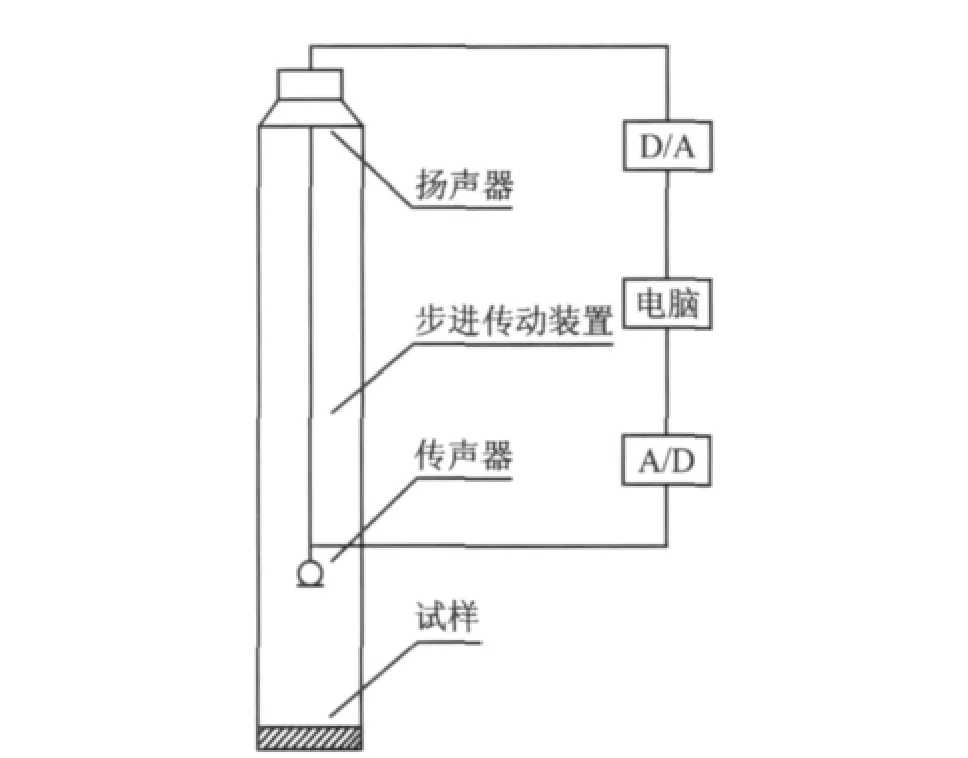
图2 测试系统示意图Fig.2 Schematic diagram of measurement system
装置为一个刚性壁面的直立式方形管道,管道横截面的口径为600mm×600mm,总长10m.声源放置在管道顶端,管道底端放置声学材料,声源面和材料面之间的有效测量距离为7m.传声器安置在管道横截面的中点,由精密步进电机驱动控制其沿轴向缓慢均匀移动,传声器测点步进移动的距离d为4cm.
表1列出了方管中各简正波模式所对应的简正频率,以及该简正波在管道横截面中点的声压分布情况.由于方管的对称性,类似(0,1)和(1,0)模式频率相等的情况,视为同一种模式.
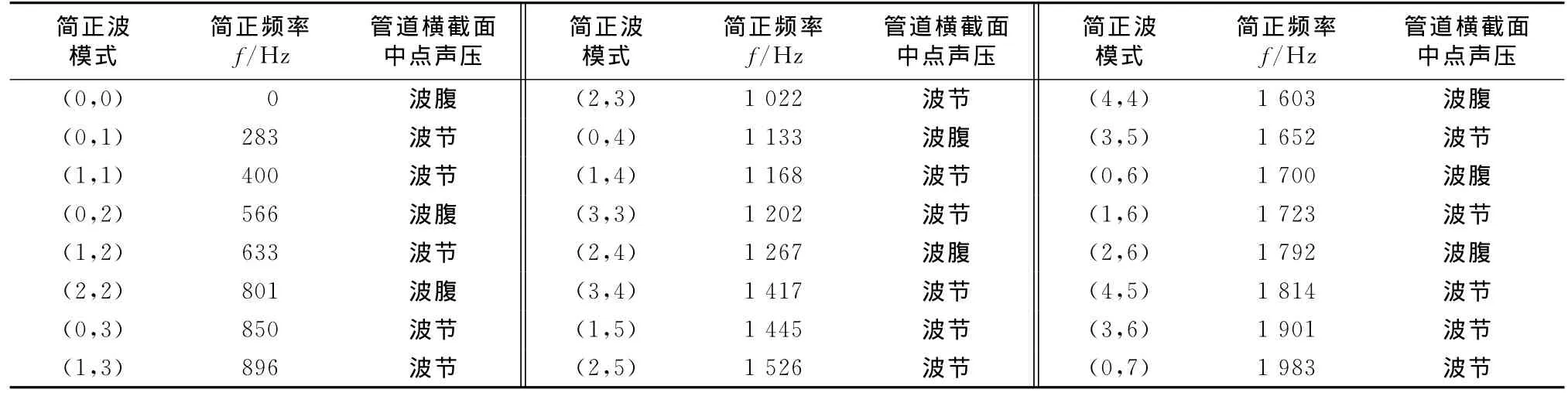
表1 600mm×600mm方管高次模式相应的截止频率Tab.1 Cut-off frequencies for the higher-order modes of 600mm square waveguide
由表1可知,方形管道对应的平面波截止频率为283Hz,在此频率以上会出现各阶高次模式声波.
试验中沿管道可得到160个测点的数据,原则上能获得80个模式的入射和反射波的复声压.在进一步的研究中,通过减小传声器步进的距离,可以获得更多的测点数据,进而增加可以分解的模式数量.
3.2 方法的检验
为了检验以上测量分解方法的有效性,对于截止频率以下的情况,采用上述方法获得的材料吸声系数与传统的驻波管法进行比较.试验在所建造的方管中进行,管道底端放置待测的声学材料.
试验使用的声源为对数扫频信号,利用上述模式分解的方法获得50~270Hz频率范围内平面波模式的入射和反射方向能量,进而计算出吸声系数.将其与传统驻波管法测量材料的吸声系数相比较.驻波管法测量采用纯音,测量了63,80,100,125,160,200,250Hz的吸声系数.图3中给出了两种方法测量结果的比较.需要注意的是,由于是在截止频率以下,模式分解法测得的结果中包含(0,0)次平面波能量和其他各高次衰减模式的能量.
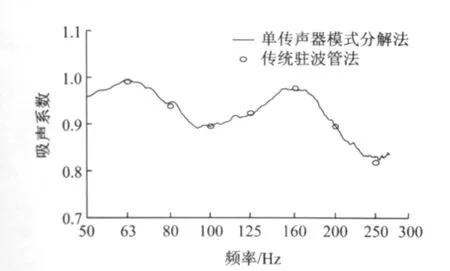
图3 传统驻波管法和单传声器模式分解法测量材料吸声系数比较Fig.3 Comparison of materials absorption coefficients by standard standing wave tube method and single-microphone modal decomposition method
由图可见,通过两种方法得到的材料吸声系数吻合良好,说明以上模式分解的测量方法是可行的.
3.3 管道内高次模式声波
当测量频率大于管道截止频率时,利用本文提出的单传声器模式分解法进行实际的测量,获得管道中入射和反射方向的各个高次模式能量分布情况.试验使用的声源为计算机生成的数字纯音信号,传声器测点布置在管道横截面的中心点,沿轴向步进移动,管道底端布置声学材料.
试验在频率为500,1 000,2 000Hz这三种情况下进行,测试结果如图4所示.图中显示了分别对应于入射波和反射波的各阶模式的能量值,并以入射方向的(0,0)模式的能量为基础进行了归一化处理.

图4 500,1 000,2 000Hz时管道内高次模式能量分布图Fig.4 Modal energy distributions at 500,1 000,2 000Hz in the waveguide
从表1中可知,在频率为500Hz时,管道内应包含3个稳定的高次模式,其中(0,0)模式在管道中心测点处声压为波腹,(0,1)和(1,1)模式在管道中心测点处声压为波节.在频率为1 000Hz时,管道内应包含8个稳定的高次模式,其中3个模式在管道中心测点处声压为波腹,其余均为波节.在频率为2 000Hz时,管道内应包含24个稳定的高次模式,其中8个模式在管道中心测点处声压为波腹,其余均为波节.由于测点沿管道中心轴线分布,对于轴线处为波节的高次模式,试验无法测得其声压值.因此,在图4中只能显示出声压为波腹的高次模式.进一步,可以采用改变传声器在管道截面上的位置,使测点位置避开波节位置,或者改变测试材料的布置方式,从而测得管道内所有模式声波的能量.
4 结语
本文提出的单传声器模式分解系统及方法可以有效地测量出管道中高次模式的声波.该方法只需使用单个传声器进行测量,避免了多传声器测量时的匹配以及对声场的干扰问题.而且,测量高次模式的数量原则上不受限制,当测点数量足够多时,通过最小二乘法处理,能够得到声场的精确结果.该方法的检验试验表明,当测量频率小于管道的平面波截止频率时,系统的测量结果与传统的驻波管测量结果相同,从而证实了这种方法的可行性.
如果测量的目的只是为了进一步研究管道底部放置材料的声学性能,则试验可以使用扫频信号进行,从而只要通过一次试验就能得到全频带的测试结果.由于目前的测量中测点沿管道中轴直线分布,因此,只适用于偶对称声场的测量.另外,由于传声器放置在管道正中心,因此对于相应波节的模式则无法测得.此时,可以采用改变传声器在管道截面上的位置,或者改变测试材料的布置方式,测得管道内所有模式声波的能量.
综上所述,利用单传声器在管道内均匀传动获得的声压信号,可以分解与测量管道内的高次模式声波,从而大幅度地拓展管道内测试材料声学特性的频率范围.除了测试材料表面的吸声性能之外,还能够得到诸如材料声阻抗、材料表面散射系数等测试结果.有关这方面的内容,将另文阐述.
[1] Moore C J.In-duct investigation of subsonic fan“rotor alone”noise[J].The Journal of the Acoustical Society of America,1972,51(5):1471.
[2] Kerschen E J,Johnston J P.A modal separation measurement technique for broadband noise propagating inside circular ducts[J].Journal of Sound and Vibration,1981,76(4):499.
[3] Salikuddin M.Sound radiation from single and annular stream nozzles,with modal decomposition of in-duct acoustic power[J].Journal of Sound and Vibration,1987,113(3):473.
[4] Salikuddin M,Ramakrishnan R.Acoustic power measurement for single and annular stream duct-nozzle systems utilizing a modal decomposition scheme[J].Journal of Sound and Vibration,1987,113(3):441.
[5] Abom M.Modal decomposition in ducts based on transfer function measurements between microphone pairs[J].Journal of Sound and Vibration,1989,135(1):95.
[6] Akoum M,Ville J M.Measurement of the reflection matrix of a discontinuity in a duct[J].The Journal of the Acoustical Society of America,1998,103(5):2463.
[7] Sitel A,Ville J M,Foucart F.Multiload procedure to measure the acoustic scattering matrix of a duct discontinuity for higher order mode propagation conditions[J].The Journal of the Acoustical Society of America,2006,120(5):2478.
[8] Schultz T,Cattafesta L N,Sheplak M.Modal decomposition method for acoustic impedance testing in square ducts[J].The Journal of the Acoustical Society of America,2006,120(6):3750.
[9] Lau S K,Leung K H.Transmission characteristics of a teejunction in a rectangular duct at higher-order modes[J].The Journal of the Acoustical Society of America,2009,126(6):3028.
[10] Moore C J.Measurement of radial and circumferential modes in annular and circular fan ducts[J].Journal of Sound and Vibration,1979,62(2):235.
