整车道路模拟试验台的控制算法

胡毓冬，周 鋐，徐 刚

（1.同济大学汽车学院，上海201804；2.同济大学新能源汽车工程中心，上海201804）

整车耐久性试验是轿车设计开发过程中最为关键的环节之一，它既是检验已有设计合格与否的有效途径，又为结构的修改和优化设计等提供客观依据.近年来，室内道路模拟试验已被广泛应用于评价整车的疲劳耐久性能.它与传统的用户道路试验和试验场道路试验相比具有更多的优点，室内道路模拟试验台架可以24小时不间断地运行，整个试验过程不需要司机的参与，而且不受天气和交通状况的影响.

室内道路模拟试验的核心在于如何在试验室环境内再现整车行驶于用户道路或试验场道路时所承受的载荷，对于疲劳耐久性试验，需要达到较高的载荷再现精度以使试验数据结果可靠.因此，使系统的实际输出加载与理想的目标加载尽可能一致就变得尤为重要.

当今行业里所采用的时域波形再现技术（time waveform replication，TWR）即是解决目标信号重现的一种方法.其理论在1976年就已经提出［1］，此后大量的商业软件相继推向市场.MTS公司于1977年推出第一版远程参数控制（RPC）［2］，Schenk公司于1979年推出传递函数迭代补偿（ITFC）［3］，Instron公司和LMS公司于1996年推出TWR［4］，这些软件都是基于相同的数学原理，即迭代自学习控制（ILC）［5］.该控制算法可以使被控系统高精度地按照要求的参考轨迹重复运行.近年来，国内各高校在该领域也进行了一些研究，其中清华大学的杜永昌等［6］研制了汽车道路动态试验模拟控制系统，此外同济大学的陈栋华等［7］、武汉理工大学的汪斌等［8］对汽车室内道路模拟试验的控制算法进行了相关研究.

随着计算机技术与现代制造业的发展，满足整车道路模拟试验的硬件系统已能比较容易获得，然而由于预算等各种因素，一些道路模拟试验系统并未配备具有迭代功能的相应控制算法软件.如果能够通过编程实现试验台的控制算法，可以大大降低道路模拟试验系统的成本，同时也为虚拟道路模拟试验台的开发提供支持.但是对于控制算法的具体实现，各公司开发的软件中算法实现的编程代码是不开放的，国内外参考文献中也少有提及.本文以同济大学汽车学院试验室的四通道整车道路模拟试验台作为研究对象，借助Matlab软件建立对目标信号进行适当重叠分段的频域迭代自学习控制算法，并在试验台上采用该算法实现对某样车轴头垂向加速度信号的时域再现.

1 TWR流程

TWR过程主要分为两大步骤，即系统辨识和目标信号迭代.

1.1 TWR系统辨识

本文所辨识的对象为四通道整车道路模拟试验系统，如图1所示.整个系统由控制器、电－液伺服控制系统、液压油缸、位移传感器、试验样车、加速度传感器等组成，辨识过程中将该系统作为一个整体进行辨识.其中，系统的输入信号为四个油缸的位移控制信号U（u1，u2，u3，u4），响应输出信号为车轮轴头处的四个垂向加速度响应信号Y（y1，y2，y3，y4）.

图1 四通道整车道路模拟试验系统Fig.1 Four－post test rig system for load simulation test

辨识方法为非参数频率响应函数（FRF）模型辨识法，具体流程如图2所示.

1.1.1 辨识激励信号

辨识中选取的辨识激励信号通常为白粉红噪声，其激励的频域范围以及激励能量值的大小需要根据所要再现的目标信号的频域信息来相应选取，而其激励能量则需与目标信号的能量相当.

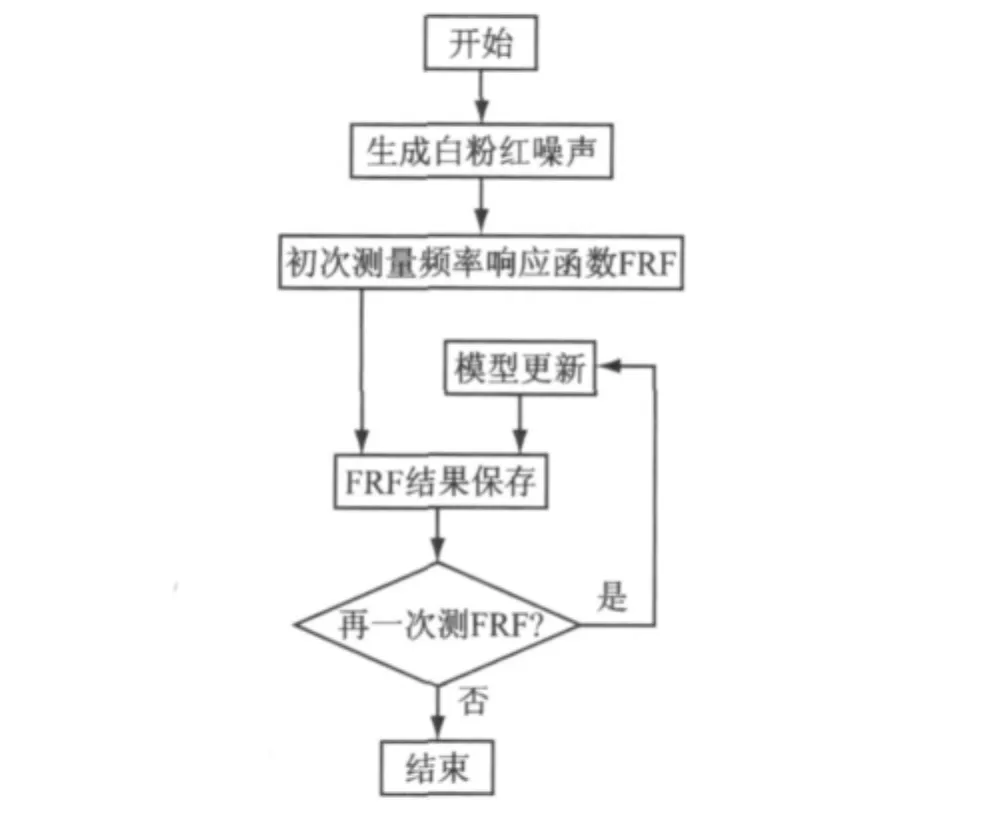
图2 FRF模型辨识流程图Fig.2 Flow diagram of the FRF model identification

1.1.2 FRF的获取

辨识中台架的激励信号（即上述白粉红噪声）是确切知道的，因而采用H1估计法来获取该系统FRF矩阵

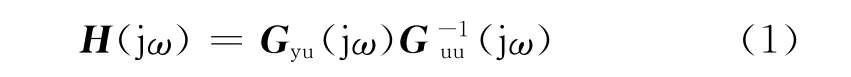
式中：H（jω）为系统FRF矩阵，Gyu（jω）为输入u和输出y在频率ω处的互功率谱估计矩阵，Guu（jω）为输入u在频率ω处的自功率谱估计矩阵.

同时可以得到各输入、输出之间的相干函数矩阵γ来评价模型对系统描述的准确程度

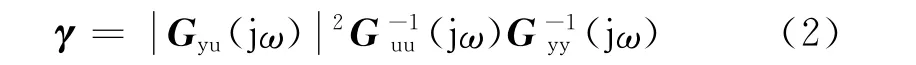
式中：γ为输入u和输出y之间的相干函数矩阵，Gyy（jω）为输出y在频率ω处的自功率谱估计矩阵.

1.1.3 模型更新

通常在辨识阶段需要进行多次模型辨识，得到对应的多个模型，对这些模型进行平均从而提高模型辨识的精度

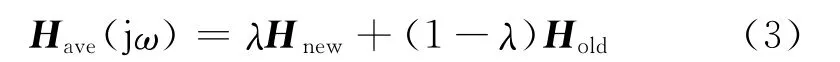
式中：Have（jω）为平均后的FRF矩阵；Hnew和Hold分别为当前次辨识和上一次平均后的FRF矩阵；λ（0＜λ＜1）为加权系数，加权系数λ通常可根据工程师的经验进行选定，或者基于相干函数来选择［9］.若更新前后的FRF变化不大，即可结束系统辨识.

1.2 TWR目标信号迭代

由于试验系统经常表现出一定的非线性，因而有必要通过迭代的方式来获得逐步收敛的驱动信号，使各目标点的响应信号逼近其对应的目标信号.本文采用的是频域迭代自学习控制算法，实际迭代流程如图3所示.

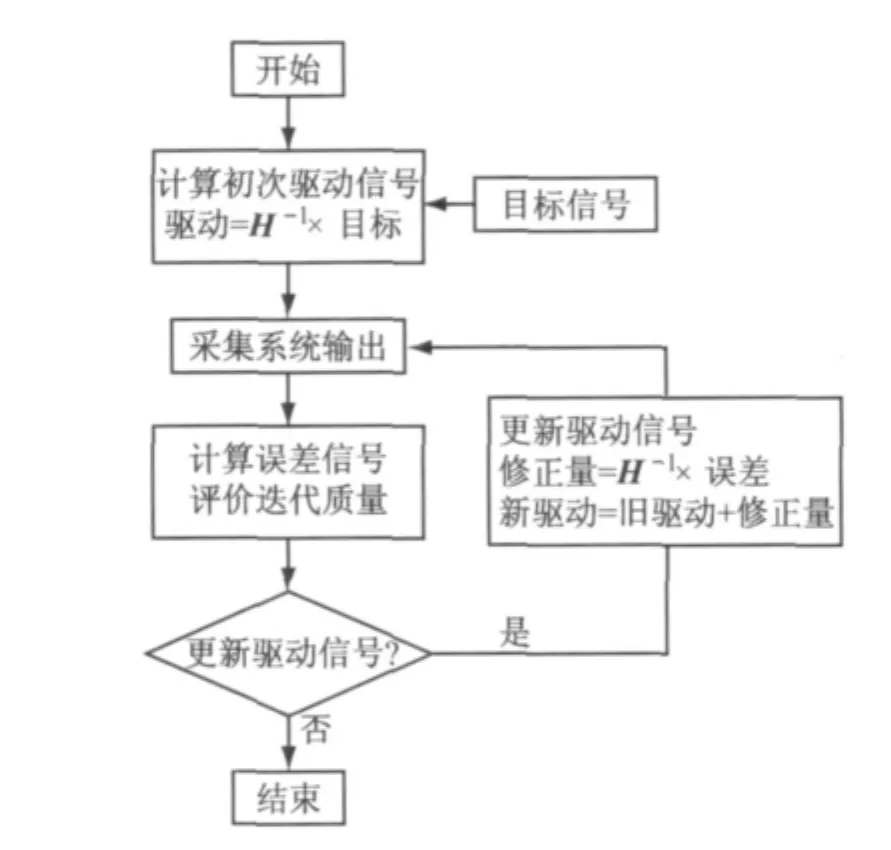
图3 迭代流程图Fig.3 Flow diagram of iteration

实际中为了避免首次驱动信号得到的系统响应大大超过目标响应信号，从而对试验系统造成破坏，另外为了防止迭代过程发散，在获得初次驱动信号矩阵时添加一个加权系数α，在频域内进行计算

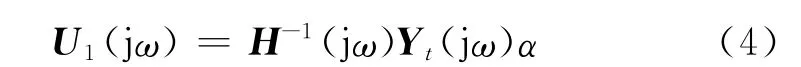
式中：U1（jω）为初次驱动信号矩阵U1（t）的傅里叶变换，可通过傅里叶逆变换得到矩阵U1（t）；Yt（jω）为目标信号矩阵的傅里叶变换；α为加权系数（0＜α＜1）.

通过播放驱动信号可得到系统实际的响应信号，进而得到各响应信号与各目标信号的跟踪误差，并且可以对迭代的质量进行评价.通常的评价指标为相对均方根值误差

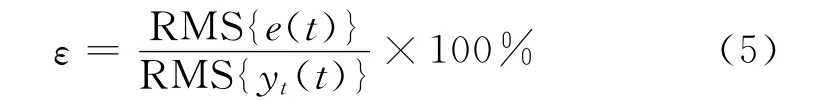
式中：e（t）＝yt（t）－y（t）为跟踪误差；yt（t）为目标信号；RMS｛｝为信号的均方根值.

通常对于整车道路模拟试验，当各ε均小于10%时即可结束迭代.否则可根据所得的跟踪误差通过计算来修正下一次的驱动信号

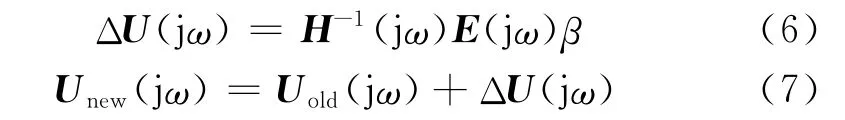
式中：ΔU（jω）为迭代中驱动信号矩阵的更新量；E（jω）为跟踪误差矩阵E（t）＝Yt（t）－Y（t）的傅里叶变换；Uold（jω），Unew（jω）分别为更新前后的驱动信号矩阵的傅里叶变换，通过对Unew（jω）进行傅里叶逆变换即可获得下一次迭代的驱动信号矩阵；β为加权系数（0＜β＜1）.

2 频域迭代自学习控制算法的实现

前文介绍了频域迭代自学习控制算法的原理及流程，接下来对该算法的具体实现做进一步的研究，进而提出在迭代过程中对信号进行适当重叠分段的改良迭代算法.

2.1 系统辨识算法的实现

由于进行系统辨识时采用的激励信号为白粉红噪声，因而在计算FRF时，为了降低随机误差，需要通过对辨识激励及响应信号进行分段计算来平滑处理.

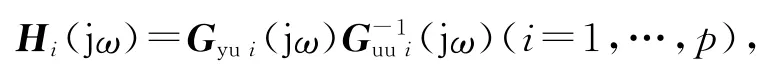
此外，为了避免由于对信号分段截取产生的能量泄漏问题，在对各段数据进行傅里叶变化时，应进行加窗处理（通常采用Hanning窗），同时在计算功率谱时对功率谱值进行加窗幅值补偿（对于Hanning窗，其补偿系数约为2.6）.

2.2 矩阵求逆的实现

在目标信号迭代过程中，需要对系统FRF矩阵进行求逆运算.对于系统FRF矩阵，可能出现矩阵奇异的情况而导致求逆过程无法进行（或接近奇异矩阵而使所得的逆矩阵不可靠），因而需要通过奇异值分解（SVD）的方法获取其最小二乘的伪逆.

若系统FRF矩阵的SVD分解为

式中：正交矩阵W的所有列向量构成了一组正交的奇异值左乘向量；对角阵Σ的对角元素包含了FRF矩阵的所有特征值，且由大到小排列；正交矩阵VT的所有行向量构成了一组正交的奇异值右乘向量.

由此可得系统FRF矩阵的逆为

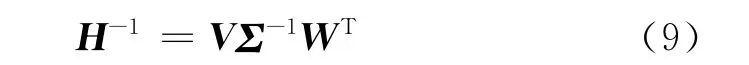
在公式（9）中仍然需要对矩阵Σ进行求逆，当Σ含有值为零的特征值（即系统FRF矩阵奇异）时求逆仍无法进行.此时可以通过在公式（9）中同时去除零值的特征值以及其对应的左乘、右乘向量，从而计算得到最小二乘意义下的伪逆［10］.

2.3 频域目标信号迭代算法的实现

频域迭代自学习控制算法要求目标信号是周期性信号，而实际的目标信号并不符合这一要求，因而需要对目标信号进行加窗处理.为了避免对目标信号的能量产生过大的削弱，本文采用自定义的衰减窗，如图4所示.即只在目标信号起始与结束的小段时间长度内对信号施加正弦衰减窗，以保证其起始和结束时刻的值均衰减为零，使其成为符合要求的周期信号，对其余的信号段则不做衰减处理.衰减时间段长度可按具体情况进行选择，本文衰减时间段选为0.5s（即信号起始与结束的100点）.

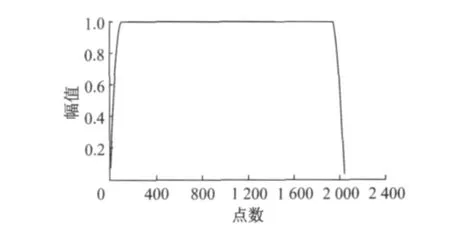
图4 自定义衰减窗图Fig.4 Custom fading window diagram

目标信号迭代通常使用的有整段迭代法和分段迭代法：① 整段迭代法即将整段目标信号直接进行频域迭代.设目标信号的点数为M，通常情况下M要远大于系统辨识中分段信号的点数N，要求所使用的系统FRF的频率分辨率为Fs／M，而经系统辨识得到的系统FRF实际分辨率为Fs／N（＞Fs／M）.通常可以通过插值的手段使原FRF频率分辨率提高到Fs／M，从而将整段目标信号直接进行频域迭代.然而，道路模拟的目标信号长度一般较大，有时会达到几十分钟甚至几个小时.在对数据量较大的数据段进行傅里叶变换时，其算法复杂度将随数据点数的增多而急剧加大，因而理论上不宜采用这种方法.②分段迭代法即对目标信号进行分段迭代，它在迭代过程中可以规避频率分辨率的问题，但是各分段起始和结束的信号段由于衰减窗的作用会出现失真，从而影响最终的迭代结果.

综合以上两种方法，提出了一种对目标信号进行适当重叠分段的方法.

首先，对时域目标信号（或时域误差信号）进行重叠分段，信号段的长度参照系统辨识划分的长度同样取为N点，重叠率通常选为50%（即N／2点），设信号分为q段（如信号总长度不是N／2的整数倍，可在信号末尾添加相应数量的数据零加以补足）；接着，将q段信号根据公式（4）（或公式（6），（7））进行频域计算（对每段信号都添加自定义衰减窗，衰减段点数选为R，使其满足2R＜N／2），得到其对应的时域驱动信号；最后，将所得的q段时域驱动信号按以下原则进行拼接，如图5所示.

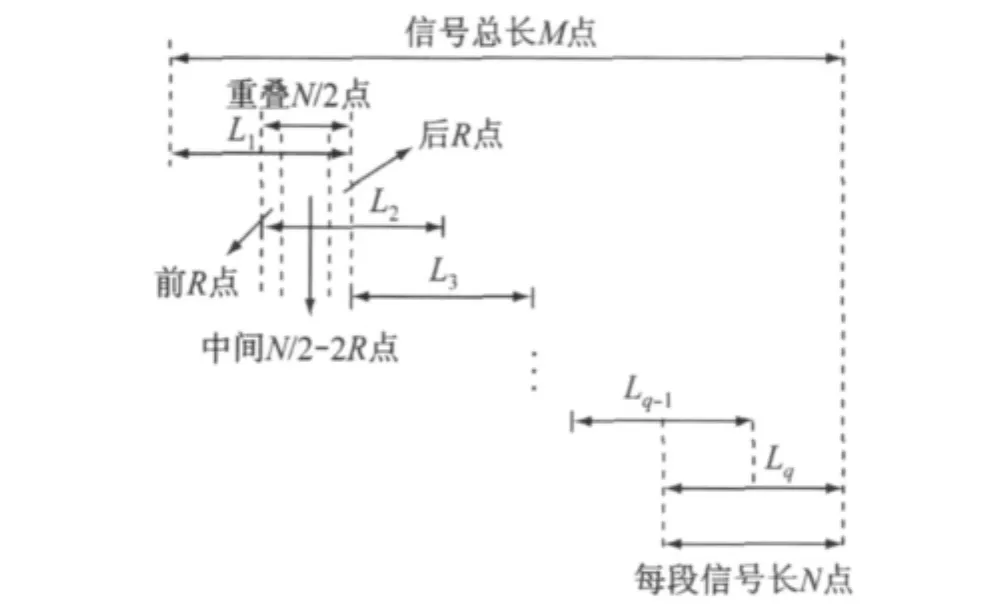
图5 改良频域迭代算法示意图Fig.5 Improved frequency－domain iterative arithmetic diagram

（1）对于没有重叠的信号段（即第一段前N／2点以及第q段后N／2点）不做处理，直接使用所得结果.

（2）对于有重叠的信号段（以第一段与第二段重叠的N／2点为例）：对于前R点，由于其在第二段的加窗处理中幅值有衰减，因而采用第一段得到的结果；对于后R点，由于其在第一段的加窗处理中幅值有衰减，因而采用第二段得到的结果；而对于剩下的N／2－2R点，由于其在两段信号的加窗处理中幅值均未产生变化，因而采用两段信号所得结果的平均值.

按以上原则即可得到时域驱动信号，使得迭代过程得以继续，并且规避了添加衰减窗对信号产生幅值衰减的影响.

3 算法验证

以现有的四通道道路模拟试验系统为对象，在真实环境中对上述频域迭代自学习控制算法进行验证.

目标信号为某样车在襄樊试车场石块路行驶时四个车轮轴头处的垂向加速度响应信号.迭代过程中通过迭代算法离线获得驱动信号，在实际试验台架上进行播放，对样车各轴头处的实际垂向加速度响应信号进行采集，借助该响应信号与目标信号的误差通过迭代算法获得下一次的驱动信号，从而建立整个迭代过程.该迭代过程中的各轴头垂向加速度相对均方根值误差收敛曲线如图6所示.

从图中可以看出，经过14次迭代后各相对均方根值误差已小于10%，已经达到试验的迭代精度要求.经14次迭代后的跟踪误差如图7所示（以左前车轮轴头处的垂向加速度响应信号为例）.从图中可以看出，实际响应信号与目标响应信号非常接近，达到了试验加载的要求.

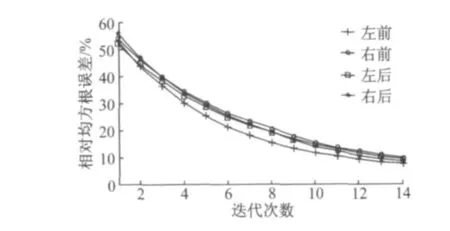
图6 迭代过程相对误差收敛曲线Fig.6 Relative RMS error convergence curve of the iteration process

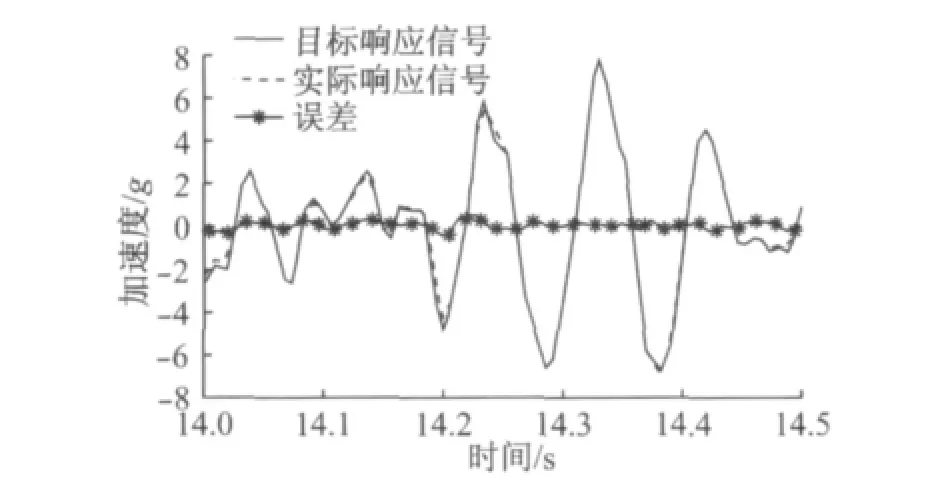
图7 第14次迭代跟踪误差Fig.7 Tracking error of the 14th iteration for the front left acceleration

4 结论

本文给出了基于FRF模型的系统辨识以及基于频域迭代自学习控制算法的目标信号迭代具体流程，提出了对目标信号进行适当重叠分段的频域迭代自学习控制算法，并对该算法的编程实现进行了深入研究.同时以现有的四通道道路模拟试验系统作为研究对象，借助Matlab软件建立了该算法，在真实环境中采用该算法进行某样车轴头加速度信号的时域再现，结果表明该算法达到道路模拟试验的加载精度要求，能够作为整车道路模拟试验台的控制算法.本文的工作对于道路模拟试验台控制算法的编制以及道路模拟试验时域信号再现加载的问题有较大帮助，同时也为虚拟道路模拟试验台的开发提供了迭代控制算法的支持.

［1］ Cryer B W，Nawrocki P E，Lund R A.A road simulation system for heavy duty vehicles［C］／／Proceedings of the Automotive Engineering Congress and Exposition.Detroit：SAE International，1976：361－374.

［2］ Dodds C J.A computer system for multi－channel remote parameter control of a test specimen［R］.Minnesota：MTS Publication，1977.

［3］ Craig J B.ITFC—how it works and where to use it［M］.Darmstadt：Schenck Publication，1979.

［4］ De Cuyper J，Coppens D.Service load simulation on multi－axis test rigs［J］.Sound and Vibration，1999，30（1）：30.

［5］ Daley S，Hätönen J，Owens D H.Hydraulic servo system command shaping using iterative learning control［C］／／Proceedings of UKACC Control 2004.Bath：UKACC，2004：117－121.

［6］ 杜永昌，管迪华.汽车道路动态试验模拟控制系统的研究与开发［J］.汽车技术，1999（3）：16.

DU Yongchang，GUAN Dihua.Study and development of vehicle road dynamic simulating test system（RDSS）［J］.Automobile Technology，1999（3）：16.

［7］ 陈栋华，靳晓雄，周鋐.汽车室内道路模拟试验系统控制算法的研究［J］.噪声振动与控制，2006，26（1）：31.

CHEN Donghua，JIN Xiaoxiong，ZHOU Hong.Study on control algorithm for vehicle road simulation test system［J］.Noise and Vibration Control，2006，26（1）：31.

［8］ 汪斌，过学迅，徐占，等.路面时域波形室内再现方法研究［J］.中国机械工程，2010，21（3）：264.

WANG Bin，GUO Xuexun，XU Zhan，et al.Research on algorithm road surface time waveform reappearance［J］.China Mechanical Engineering，2010，21（3）：264.

［9］ De Cuyper J，Coppens D，Liefooghe C，et al.Advanced drive file development methods for improved service load simulation on multi axial durability test rigs［C］／／Proceedings of the Acoustics and Vibration Asia.Singapore：Acoustics and Vibration Asia，1998：339－354.

［10］ Maia N M M.An introduction to the singular value decomposition technique［C］／／Proceeding of the 7th International Modal Analysis Conference.Las Vegas：［s.n.］，1989：338－339.