粒子滤波在机动目标自适应参数辨识算法中的应用

叶利民

（海军工程大学研究生院，湖北武汉 430033）

0 引言

随着反舰导弹性能和突防技术的不断提高，水面舰艇拦截反舰导弹变得更为困难。目前世界上许多国家均开始研发速度达2 Ma以上的超音速反舰导弹，而且攻击模式也趋于多样化，如水平机动、掠海飞行、跃升俯冲攻击等，其中，末端超音速、跃升俯冲攻击模式是现代导弹极具杀伤力的突防方案，而当前的目标跟踪算法由于预置模型的局限性和目标运动的不确定性，对诸如上述高速强机动攻击模式的跟踪性能大大降低，无法满足舰艇反导作战的要求［1－2］。

目标自动跟踪系统显著提高了武器系统在战场上的作战能力与适应能力，它所采用的机动目标模型应是多模态的。机动目标参数辨识模型正是一种多模态模型，它是利用自适应滤波的思想，通过状态滤波估计的输出特性，构建信息反馈通道，动态地辨识机动目标的机动参数，但其对于非线性较强的系统辨识能力较差。粒子滤波算法是非常适合于非线性、非高斯系统的一种滤波算法。粒子滤波算法于20世纪50年代提出，60年代得到进一步发展，但一直受到粒子数匮乏和计算机处理能力的限制。直到1993年，Gordon等提出了一种新的基于Bootstrap的粒子滤波算法［3］，才真正奠定了粒子滤波算法的基础。粒子滤波的思想本质是用1组带有权重值的随机采样点的离散和来计算难于处理的积分形式的后验概率密度函数，并基于这些采样点和权重值来计算状态值。根据大数定理，当随机采样点足够多时，粒子滤波算法可以基本不失真的表示状态的后验概率密度函数。粒子滤波算法也包括预测阶段和更新阶段，与卡尔曼滤波算法不同的是，它不需要依赖于系统方程和测量方程的线性程度和状态的分布，克服了以往基于线性高斯滤波的缺点，其主要优点包括:

1）可以表示任意的概率密度函数;

2）对状态空间的可能区域进行自适应的关注;

3）可以处理非高斯的系统噪声;

4）滤波框架可以实现对机动目标的跟踪。

本文通过将以往参数辨识过程中的卡尔曼滤波器换为粒子滤波器，发挥粒子滤波可以对非线性非高斯噪声系统进行滤波的特点，结合参数辨识的递推最小二乘算法，提出了一种机动目标自适应跟踪算法。仿真实验说明了该算法的有效性。

1 模型建立

1.1 基于参数估计模型的递推算法

在连续的时间域中，以三阶线性微分方程结构确定待估计的机动目标运动模型的结构［4］为:

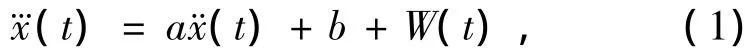
其中:a和b为待估计的模型参数;W（t）是均值为0的白噪声。

由于要通过模型参数a和b的估计来实现模型的估计，它的状态方程为:

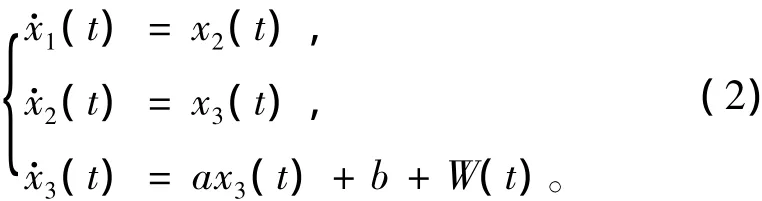
由参数估计模型的表达式（2）可以看出，参数a和b综合决定了目标加速度的变化率。b是变化率中的常数，单位是m/s3，a是相对于加速度的机动系数，一般情况下是1个小于0的负数，单位是1/s。

依据参数a和b的不同组合，将使参数估计模型的结构可以覆盖机动目标可能的多种运动状态。

上述参数估计模型对目标的多种运动模态的广泛适应能力，使得它不仅具有对采样周期变化的适应能力，而且在它的有效动态递推估计算法中通过参数a和b的自动校正，还能自动适应机动目标运动模态的变化，不需要像IMM算法那样，需要对机动目标多种运动模型之间的转换规律进行人为的假定和估计。上述模型的特性为自适应滤波的实现提供了基本条件，利用目标运动信息估计得到参数a和b，获得下次滤波的模型，原理如图1所示。

依据参数估计模型（2），以求解微分方程的欧拉算法的二步格式和中心差商的数值微分算法为基础，实现微分方程的动态估计。在一维的情况下，将待估计的参数估计模型的结构表示为:

图1 自适应滤波原理框图Fig.1The principle of adaptive filter

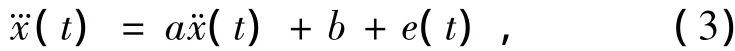
其中，e（t）为模型的残差。

模型的状态方程为:

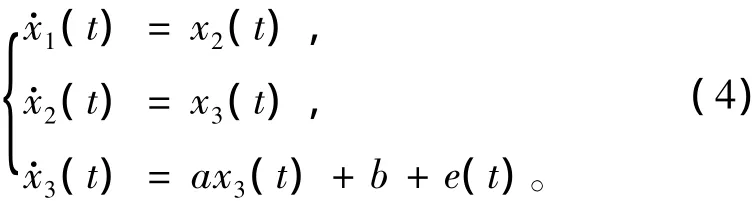
根据求解微分方程的二步格式的欧拉算法，选定步长为h，对状态方程式（4）进行线性变换，

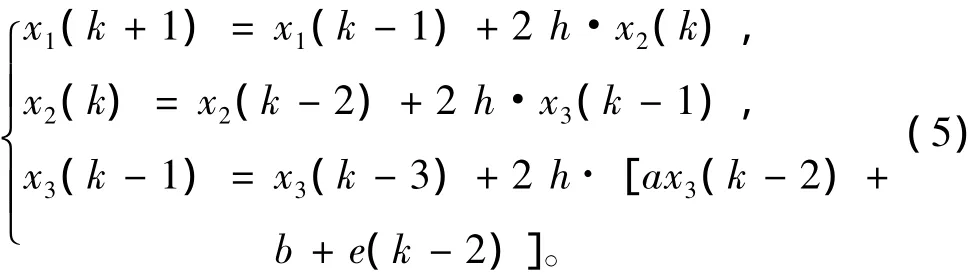
其中:k为步长为h的时间序号。

利用差商数值微分公式有

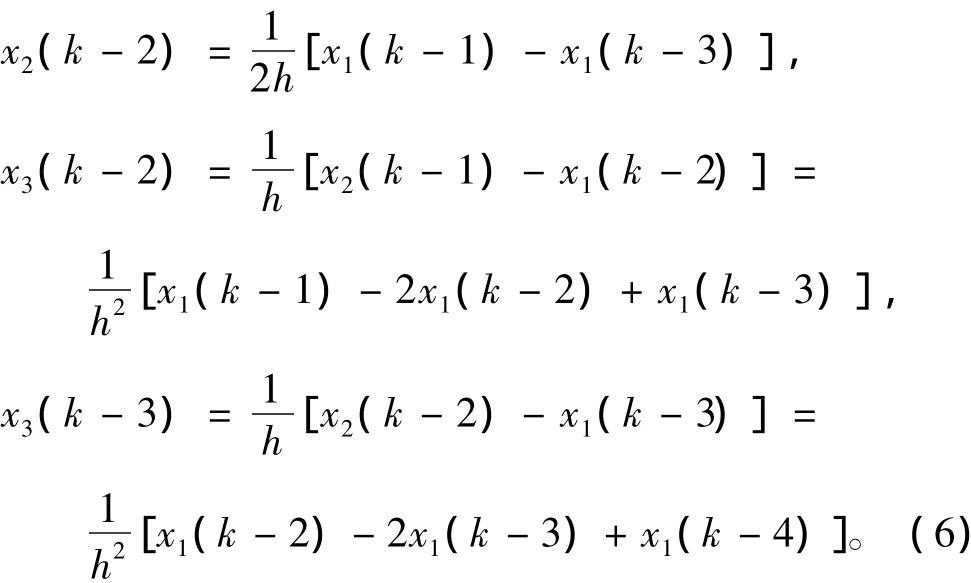
将式（6）代入差分方程组（5），由下向上迭代化简得:

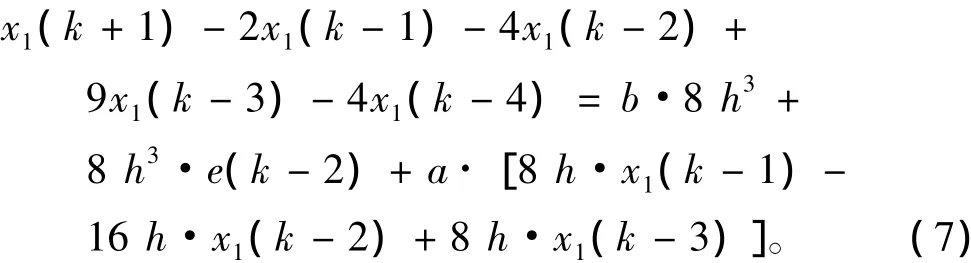
令x（k）=x1（k），得到以待估计参数a和b为变量的线性方程:

线性方程式（8）中各已知量之间的变换关系式为:

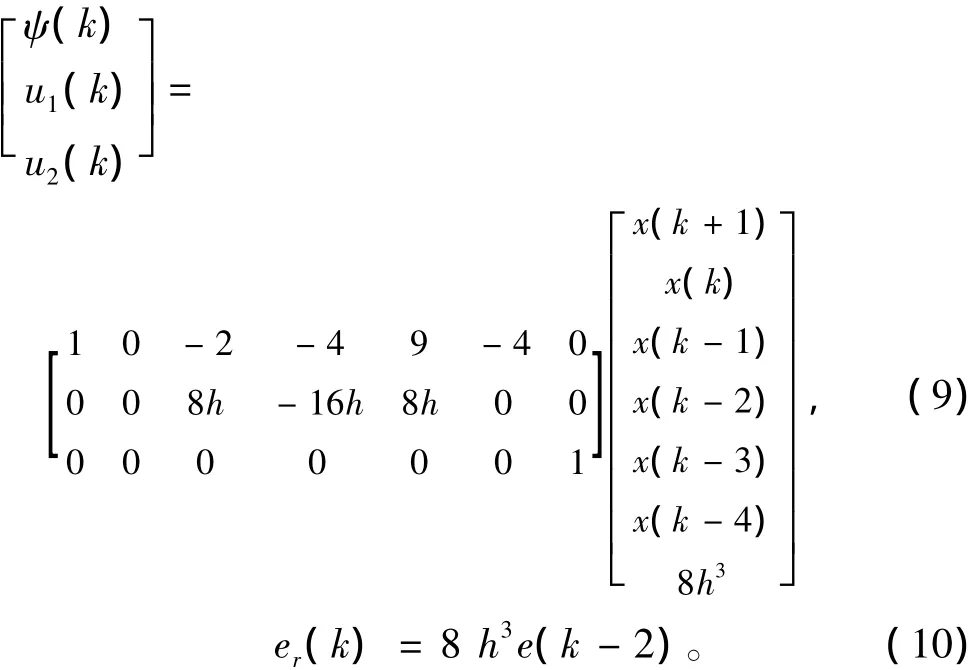
当系统动态观测到目标位移量序列值x（－3），x（－2），x（－1），x（0），…，x（m+1），m≥2，则可按式（8）顺序构造出如下线性方程组:

极小化指标函数J，即可得到目标“参数估计模型”参数θ的最小二乘解

只要UTU非奇异，就有惟一解，这在通常的动态观测中是可以满足的。因此，利用线性变换式（9），就可实现“参数估计模型”的动态估计。而且，模型参数θ的估计，还可采用递推算法，这正是自适应滤波所必需的。

对于用m个方程所得的解，记为

1.2 引入粒子滤波的自适应滤波算法

基于贝叶斯滤波思想，粒子滤波（Particle Filters）通过带有归一化权值的粒子集来近似表示后验概率密度。当粒子采样数量足够大时，能准确地表达后验密度分布，此时的粒子滤波算法接近贝叶斯最优估计。每个粒子的位置和权重反映了状态空间在该区间的密度［5－7］。设采样N个粒子粒子滤波算法原理描述如下式:

在通常情况下，建议将密度函数分解为:

根据贝叶斯公式，后验概率密度可表示为:

需要说明的是，与上面讨论的递推贝叶斯估计的假设相同，这里的建议密度函数同样服从一阶马尔科夫过程，且已知观测独立于指定状态。根据贝叶斯估计原理，粒子滤波的过程可分为以下2个阶段:

1）预测阶段

预测阶段是先验概率在状态空间进行搜索的过程。从过程噪声ωk－1中采样N个点，使用这些点通过状态方程形成新的粒子分布，其计算公式为:

2）更新阶段

当得到k时刻的观测值，将式（20）和式（21）代入权重计算式（19），可以得到粒子权重

通常需要对上面计算的权重进行归一化得到权重

上述方程式构成了递推的PF算法的基本过程。通过上述推导过程可以看出，粒子滤波不受线性高斯条件的约束，易于非线性非高斯跟踪算法的实现。

通过将参数估计的递推最小二乘滤波算法和粒子滤波算法结合起来，可以实现自适应估计滤波，由滤波输出结果估计得到参数a和b，由参数a和b确定粒子滤波算法中目标模型的状态转移矩阵，如此循环计算，算法流程如图2所示。

2 仿真实现

利用Matlab软件，采用蒙特卡洛法进行仿真实验。

2.1 初始设定

图2 基于参数估计模型的滤波算法实现流程图Fig.2The flow chart of realizing the filtering algorithm based on parameter identification model

设目标在做角速度恒定的转弯运动:初始斜距600 m;距我舰初始方位角0.785 rad;变化率1 rad/s;速度为850 m/s;雷达采样率为50 Hz;采样持续时间10 s;观测距离随机误差5 m;观测方位角随机误差0.9 mrad。

2.2 仿真结果及分析

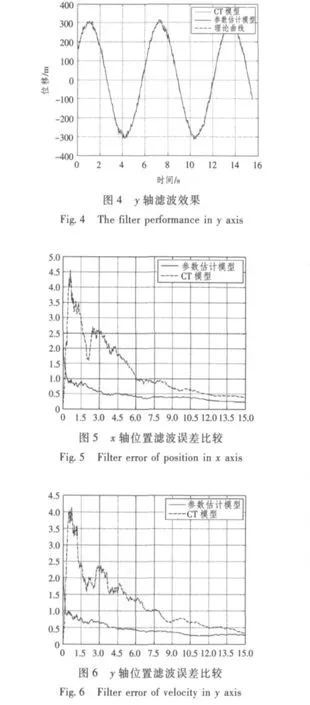
分别用CT跟踪模型以及基于粒子滤波算法和递推最小二乘算法的目标参数估计模型对目标进行跟踪，仿真结果如图3～图6所示。

由仿真结果可以发现，本文提出的算法对机动目标的跟踪效果要好于用单一模型进行跟踪的效果。本文所提模型既可动态地进行识别，又具有对工作周期变化的适应能力，可以覆盖机动目标可能的多种运动状态，使自适应滤波问题可在正常的技术思路下进行。仿真结果表明，此模型在原理上是正确的，在计算上是可行的，滤波器能较快收敛，计算精度高，反应时间短，在解决机动目标跟踪问题上，效果较好。

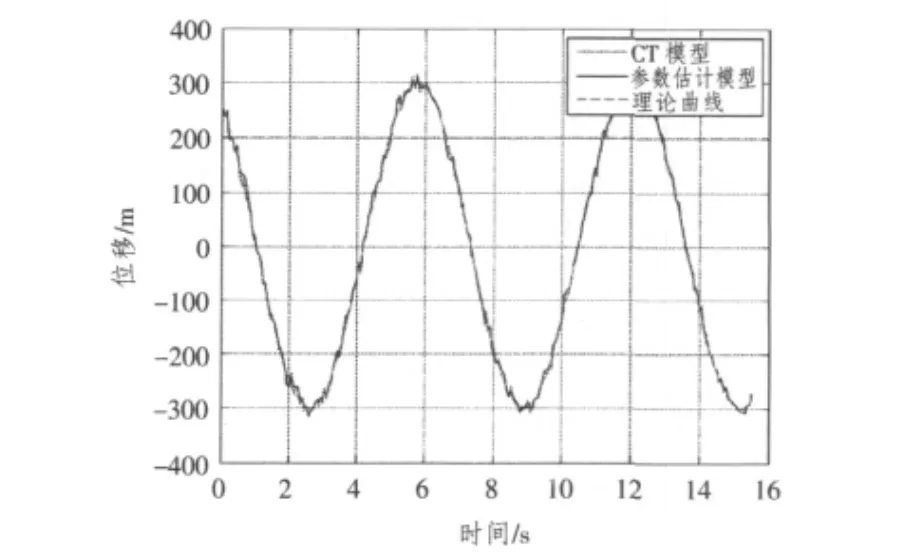
图3 x轴滤波效果Fig.3The filter performance in x axis

3 结语

本文针对反舰导弹末端机动问题，通过对参数自动辨识模型进行改进，引入对非线性非高斯噪声系统有良好跟踪效果的粒子滤波算法，提出了一种新的参数辨识模型。并在目标作匀速圆周运动的情况下进行了算法的跟踪性能仿真试验，试验结果证实了算法的有效性，具有一定工程实际意义。

［1］LI X R，JILKOV V P．A survey of maneuvering target tracking partⅠ:dynamic models［J］．IEEE Trans．Aerospace and Electronic Systems（S0018－9251），2003，39（4）:1333－1363．

［2］LI X R，JILKOV V P．A Survey of maneuvering target tracking partⅡ:ballistic target Models［C］//Proc．2001 SPIE Conf．on Signal and Data Processing of Small Targets，San Diego，CA，USA．USA:SPIE Press，2001，4473:559－581．

［3］GORDON N J，SALMOND D J，SMITH A F M．Novel approachtononlinear/non-GaussianBayesianstate estimation［J］．Proceeding of the IEEE，1993，140（2）:107－113．

［4］王志贤．最优状态估计与系统辨识［M］．西安:西北工业大学出版社，2004．181－219．

［5］CRISAN D，DOUCET A．A survey of convergence results on particle filtering methods for practitioners［J］．IEEE Transaction on Signal Processing，2002，50（2）:736－746．

［6］KALMAN H S．Filtering and neural networks［M］．New York:John Wiley and Sons，2001．

［7］LIU J S，Chen R．Sequential monte carlo methods for dynamical systems［J］．Journal of the American Statistical Association，1998，93（5）:1032－1044．