横向干货补给系统高架索的静力学分析
2012-03-07马仁刚张良欣何学军
马仁刚,张良欣,何学军
(海军工程大学后勤指挥与工程系,天津 300450)
0 引言
航行横向补给[1]是海上物资、装备补给和人员换乘最重要的手段之一,在海军后勤保障方面发挥着不可替代的作用。高架索补给系统是船舶补给最为常用的一种[2]。跨接于补给船和接收船之间的高架索道系统是最直接的承载系统,其受力状况将直接影响系统传输过程的安全性、高效性。研究高架索的静力学特性,对于合理设计补给装置系统,增加系统稳定性及增强补给能力提供必要的技术支持和理论依据。
目前,国内外关于航行横向补给的文献很少,已有文献以工程技术应用研究居多。卢永锦[3]利用弹性力学原理建立了海上横向补给过程中高架索道系统的静态分析模型和动态特性模型,并推导出了介于近似法和精确法之间的一种计算方法。阎宏生、余建星等[2]利用弹性力学的有关理论,给出了针对轻型高架索系统的一种力学分析模型。余建星、李红涛[3]针对现有高架索补给系统对补给中关键参数进行计算,提出适合小型船舶补给作业的补给系统。任爱娣、张良欣等[4]基于抛物线理论对海上横向干货补给高架索索道系统的静力学问题进行理论推导和分析。上述文献得到了高架索张力与挠度的关系表达式,但忽略了挠曲对高架索长度影响,将高架索发送端至接收端视为一直线段进行分析求解。本文针对航行横向干货补给系统,考虑了高架索挠曲对索长的影响,在集中荷载处将高架索分为S1和S2两段考虑,利用微元法得到了更为精确的高架索挠度表达式,将其进行二阶泰勒展开并代入悬挂点轨迹方程,重点研究了补给过程中货物运输的安全性,通过数值计算发现补给过程中的落水危险点并不会发生在最大挠度处,而更接近接收端;研究了高架索张力和补给距离对高架索静挠度的影响。
1 张力—挠度方程的推导
1.1 基本假设
1)高架索为绝对柔性构件,只承受沿索轴向张力,不承受剪力和弯矩[5];
2)忽略高架索张力引起的轴向变形量;
3)高架索质量均匀分布,索上各点具有相同的物理性质。
1.2 静力学基本方程建立及求解
高架索空间位置、受力状况以及变形如图1所示。h为高架索发送端与接收端高度差;L为横向补给距离;XQ为集中荷载作用点距发送端的水平距离; fQ为载荷点高架索的静挠度;q为高架索自重产生的均布荷载;Q为集中质量引起的静荷载;TA和TB为高架索发送端和接收端张力;HA和HB为高索发送端和接收端水平张力;VA和VB为高架索发送端和接收端垂直张力。
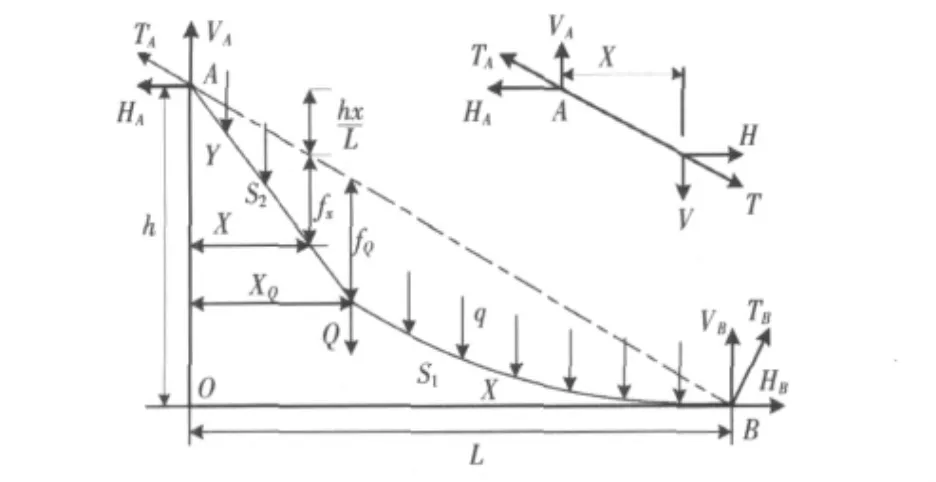
图1 横向补给系统高架索受力图Fig.1The load condition of highline cable of alongside replenishment system
由静力平衡条件∑MB=0可得:


将集中荷载Q左端AQ段上距支承点A水平距离为X处截断,取左端为研究对象,有:
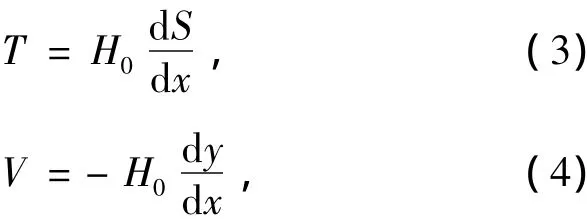
式中:S为索道弧线长度;x和y为索道AQ段上任意点的坐标值。由平衡条件∑V=0可得:

2 算例
2.1 补给过程中货物运输的安全性分析
设L=40 m,h=10 m,q=40 N/m,Q=5 kN,TA= 20 kN。式(9)为隐函数表达式,将上述数据代入式(9),fQ和XQ按二阶泰勒展开,可得:
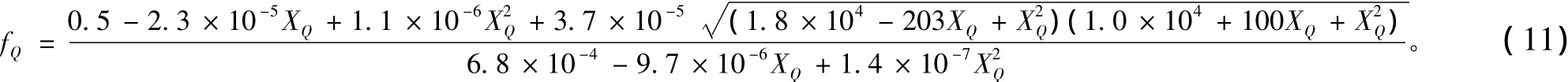
由式(8)可得:

将式(11)代入式(12),并求极值得出XQ= 34.67 m时,y取得极小值,此处即是货物运输过程中的落水危险点。由图2可见,在整个补给过程中,悬挂点处挠度为近似对称抛物线,且最大挠度出现在XQ=20 m附近。在实际补给过程中,落水危险点并不会发生在高架索最大挠度附近,而发生在低于且接近接收端处,如图3所示。

2.2 主要参数对高架索挠度影响
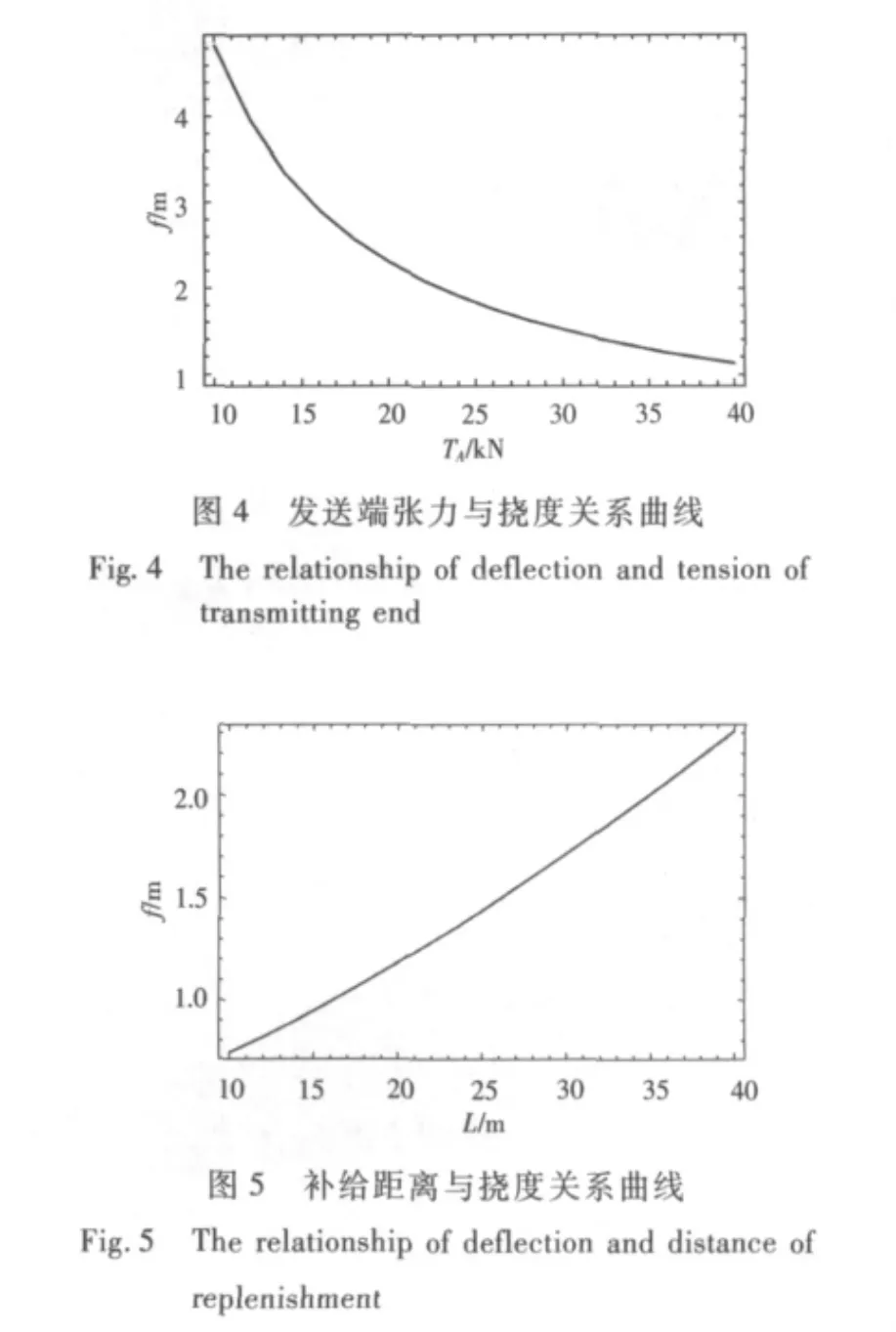
进行参数分析时,取集中荷载位置位于XQ= 0.75 L处,除可变参数外,其余数据均采用上节数据。图4和图5分别描述了补给过程中发送端张力和补给距离对高架索挠度的影响。由图中可以看出,张力对高架索挠度影响较大,高架索挠度随发送端张力增大有大幅度减小,当发送端张力大于35 kN时,其挠度变化有渐缓趋势。在实际补给系统中,使用的经验认为索道发送端恒张力与在索道上输送的货物重量有关,即荷/张比,其值一般在1:4左右[6];补给间距对挠度影响也不小。一方面,从补给装置本身设计的角度出发,希望距离越小越好,这样装置既经济又易于实现;另一方面,从使用的角度出发,则希望距离越大越好,这样既便于操作又有利于保证船舶安全。由图5可知,在横向补给距离为20~40 m范围内,补给距离与高架索挠度关系呈现近似线性特征。为了减少航行补给过程中补给船与接收船相互干扰,实际系统必须满足横向补给俯角小于30°条件,即h=10 m时,补给距离L应大于17.3 m。目前国外的经验一般确定补给船距为40~60 m。
3 结语
本文从静力学角度出发,利用微元法得到了更为精确的高架索挠度表达式和悬挂点轨迹方程。通过算例可知,补给过程中的落水危险点并不会发生在高架索最大挠度附近,而更接近接收端。对于本文给定的数据,货物运输过程中的落水危险点在距发送端34.67 m附近。同时研究了高架索张力和补给距离对高架索静挠度的影响,发现张力对高架索挠度影响较大。
[1]卢永锦.海上横向补给高架索道系统数学模型研究[J].中国造船,1996,37(1):17-22.
LU Yong-jin.A study on mathematical model of highline system for transverse replenishment at sea[J].Shipbuilding of China,1996,37(1):17-22.
[2]阎宏生,余建星,郭海涛.海上轻型高架索补给系统的力学分析及安全性研究[J].海洋技术,2006,25(2):39-43.
YANHong-sheng,YUJian-xing,GUOHai-tao.The mechanics analysis and safety research of the light highline replenishment system[J].Ocean Technology,2006,25 (2):39-43.
[3]余建星,李红涛.高架索海上补给装置在小型船舶补给上的应用[J].海洋技术,2005,24(2):59-62.
YU Jian-xing,LI Hong-tao.Application of highline system for replenishment at sea in replenishment for small-scale ships[J].Ocean Technology,2005,24(2):59-62.
[4]任爱娣,张良欣,何学军.高架索索道系统研究中的恒张力假设[J].舰船科学技术,2010,32(2):27-31.
REN Ai-di,ZHANG Liang-xin,HE Xue-jun.Constant stress consumption in the research of highline system[J].Ship Science and Technology,2010,32(2):27-31.
[5]周继祖.线缆吊车[M].北京:中国铁道出版社,1986.
ZHOU Ji-zu.Cable crane[M].Beijing:China Railway Press,1986.
[6]严梅剑.海上航行横向补给装置选型设计[J].船舶,2004,(1):51-53.
YAN Mei-jian.Type selection and design of alongside replenishment device[J].Ship&Boat,2004,(1):51-53.
