水下非接触爆炸作用下舰船结构损伤评估

李志辉，刘辉，李其修，吴向君

（海军工程大学船舶与动力学院，湖北武汉 430033）

0 引言

鱼雷、水雷和深水炸弹等武器均在水中爆炸。这些武器的主要破坏形式是非接触爆炸。二战期间，为了应对非接触爆炸及其对舰船的机器和设备的冲击破坏，急需了解水下爆炸产生的效应［1］。因此，各国均大力开展了水下爆炸方面的研究，特别是美国、英国和德国。随着计算机技术的不断提高，舰船和设备水下爆炸动态响应的理论分析和计算也广泛开展。但是由于水下爆炸和舰船结构动态响应的复杂性，水下爆炸作用下舰船结构损伤研究主要来自于对试验现象或实验数据的分析［2－3］。本文在考虑水下爆炸冲击波和二次压力波的同时也考虑了气泡脉动和冲击波引起的反射波对舰船结构的影响，在综合分析的基础上建立了舰船结构的损伤等级，确定等级评估标准，并举例与模拟实验情况下舰船结构损伤情况进行对比。

1 舰船结构响应控制方程

水下爆炸时，冲击对舰船结构的响应可以通过双重渐近近似（DAA）方程［4］来表示，舰船结构响应的离散差分方程可表示为

式中:x（t）为结构位移矢量;Ms，Cs和Ks分别为质量、阻尼和刚度系数;f（t）为外力矢量。对于声波对舰船结构的激发响应，f（t）可表示为

式中:pi（t）和ps（t）分别为流体网格的节点和散波压力向量;fd（t）为干式结构的附加力向量;Af为节点压力与节点力相互转换的对角矩阵;G为联系流体与结构表面力的变换矩阵。

双重渐近近似的一阶微分方程可表示为

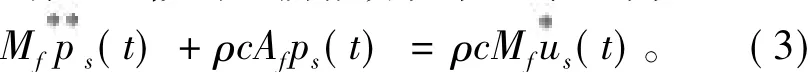
式中:ρ和c分别为流体密度和声速;us（t）为流体散波速度向量。

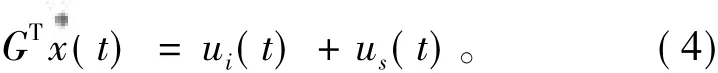
假设fd（t）为0，把式（2）代入式（1），式（4）代入式（3），得:

通过式（5）和式（6）便能求解爆炸瞬时的x和ps。

2 水下非接触爆炸损伤因子

2.1 水下非接触爆炸的冲击压力

2.1.1 水下非接触爆炸的峰值压力

由于水下爆炸时静态压力的叠加而产生水下冲击波，爆炸时冲击波压力p（t）瞬时增加至峰值pmax，随后以指数规律衰减［5］，因此冲击波压力可通过Cole经验公式表示为

式中:pmax为冲击波抵达舰船时的峰值压力;t1=R/C，t1为冲击波抵达舰船的时间;λ为指数衰减时间常数。

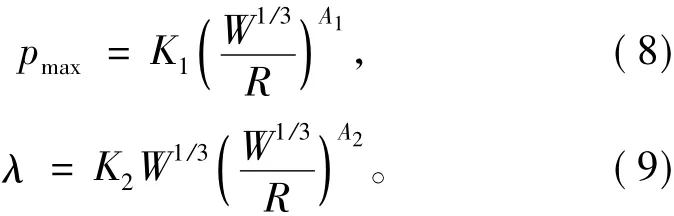
峰值压力和指数衰减时间常数主要取决于炸药的重量以及炸药距舰船的距离。峰值压力pmax和时间衰减常数λ可由下述公式表示:式中:K1，K2，A1和A2为常数，其大小取决于炸药的类型，具体几种类型炸药的参数如表1所示;W为炸药的重量，kg;R为炸药和目标之间的距离，m。

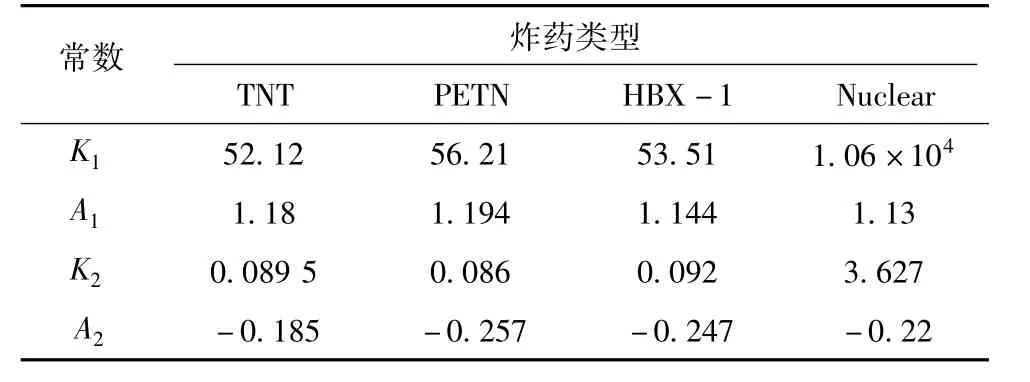
表1 不同类型炸药的冲击波参数Tab．1Shock wave parameters for various explosive charges

2.1.2 水下非接触爆炸的反射波压力

当水下爆炸产生的冲击波破坏舰船时，冲击流体和结构相互作用形成的反射压力可以用泰勒公式进行合理和准确的预测。对于舰船某区域遭受压力波压力ps（t）冲击时，产生的反射波压力pr（t）也同时作用于此区域。假设舰船某区域的损伤速度为vf（t），通过牛顿第二运动定律，可得

式中:vs（t）和vr（t）分别为冲击波速度和反射波速度，则舰船某区域的损伤速度由下式表示:

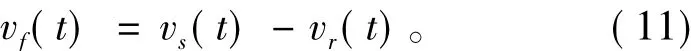
冲击波压力和反射波压力可以通过ps=ρfcvs和pr=ρfcvr进行描述。式中ρf和c分别表示海水密度和声速，则

2.1.3 冲击因子

当舰船航行过程中遭受水下爆炸时，破坏程度会受到炸药的重量、炸药距舰船的距离、炸药攻击方向等因素的影响［6］。通常舰船遭受水下爆炸的破坏程度由冲击因子表示，而冲击因子与冲击波的能量密度成正比。冲击波能量流量密度可由下式表示:

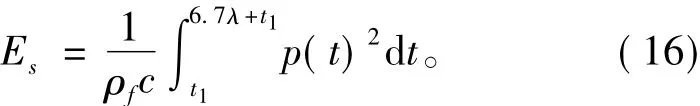
将式（7）代入式（16），

假设炸药距舰船距离为R，炸药重量为W，则Es可以近似表示为

从式（18）可以看出，能量流动密度取决于炸药距舰船距离R和炸药重量W的大小，因此可以定义1个因子来表示舰船的破坏程度。对于水面舰船，定义龙骨冲击因子（KSF）来衡量舰船遭受水下非接触爆炸时冲击波对舰船的破坏程度，即

式中，θ为炸点到舰船龙骨方向与垂直方向的夹角，如图1所示。

图1 龙骨冲击因子的定义Fig.1The definition of KSF

2.2 气泡脉动和二次压力波

2.2.1 气泡脉动

试验数据［7］显示，炸药水下爆炸时在水中形成的气泡在压力作用下迅速膨胀和压缩脉动，每次脉动将损失部分能量，能量具体的分散形式如表2所示。

表2 水下非接触爆炸能量分散形式Tab．2Energy distribution of underwater explosion

水下爆炸时，由于高温和高压产生大量气体，并产生冲击波，其中大约一半的能量以冲击波形式释放。气泡具体脉动过程如图2所示。水下爆炸后气泡脉动周期T和最大半径Rmax可由下述公式表示:

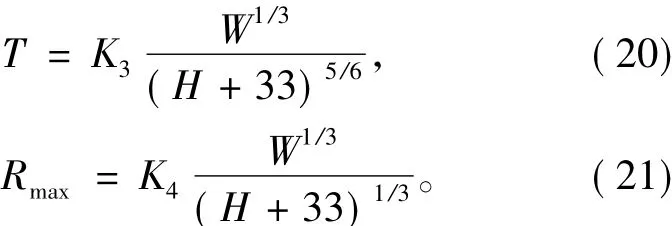
式中:H为炸药所处深度;K3，K4为常数，具体数值见表3。

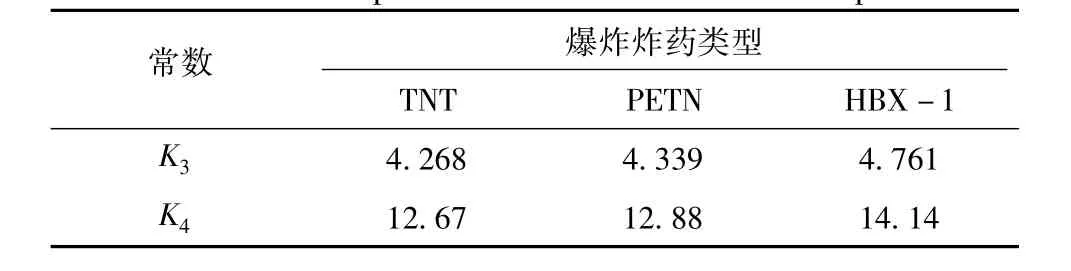
表3 水下爆炸气泡脉动常数Tab．3Bubble-pulse constants of underwater explosion

通过文献和实验数据可知，二次压力波最大压力pm可由下述公式表示:

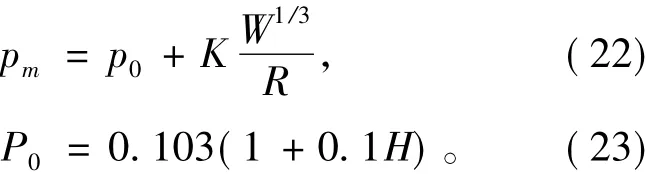
式中:p0为炸药在水中的绝对压力;H为炸药在水中的深度;K为常数。

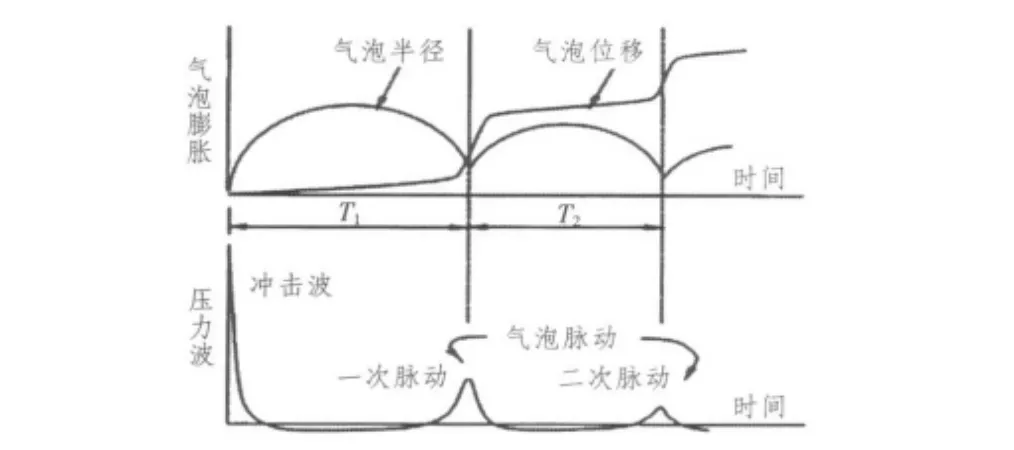
图2 水下爆炸的气泡膨胀和脉动过程Fig.2Gas bubble growth and bubble-pulse of underwater explosion

2.2.2 气泡脉动因子

炸药在水下爆炸时，气泡能通过爆炸产生的气体产物克服静水压第一次膨胀达到最大值时所做的功来度量［8］，即

由于气泡脉动对舰船的破坏作用主要取决于气泡能的流动密度，所以可定义气泡能流密度为

将式（21）中的Rmax和式（23）中的p0代入到式（25），可得

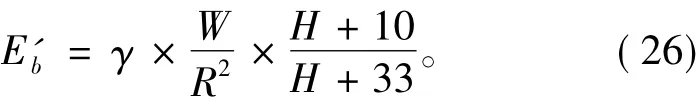
式中:γ为常数;R为炸药离舰船的距离;H为炸药在水中的深度。综上，可把气泡脉动因子（BPF）定义为另一个表示破坏程度指标。对于水面舰船，H近似等于R，则

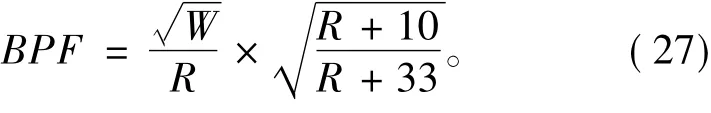
3 舰船结构损伤等级

3.1 舰船结构损伤等级

通过大量模拟实验和舰船遭到水下非接触爆炸时的损伤情况，可把水下非接触爆炸作用下舰船结构损伤等级划分为6个（S1，S2，S3，S4，S5，S6）。具体等级划分见表4。

表4 舰船结构损伤等级的定义Tab．4Damage grade of ship structure deformation

3.2 舰船结构损伤等级评估标准

从2.1节和2.2节分析可知，水下非接触爆炸作用下舰船结构损伤主要来自水中冲击波和气泡脉动。通过前文可以用冲击因素KSF来衡量冲击波对舰船结构的损伤严重性指标，用BPF来衡量气泡脉动对舰船结构的损伤严重性指标。因此，可以依靠KSF和BPF两个指标来评估水下非接触爆炸作用下舰船结构的损伤情况。以2 000 t左右的水面舰船遭受TNT炸药爆炸为例，通过大量实验和数据模拟，其结构损伤评估标准如图3和表5。

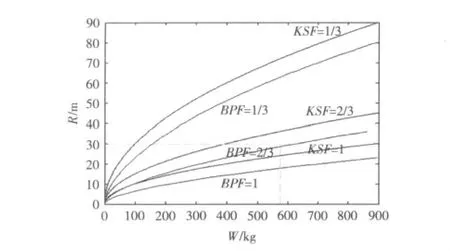
图3 舰船结构损伤等级评估标准图Fig．3Assessment standard of ship structure deformation

表5 舰船结构损伤等级评估标准Tab．5Assessment standard of ship structure deformation

4 实例分析

本文以2 500 t水面舰船遭受水下非接触爆炸为例，长100 m，宽14 m，高8 m，其他结构参数见表6。若舰船遭受TNT炸药爆炸破坏，通过表1和表3可知，K1，K2，A1，A2，K3，K4分别为52.12，1.18，0.089 5，－0.185，4.268，12.67。本例中，KSF= 0.8，BPF=0.64，炸药重量为576 kg，炸药距舰船的垂直距离为30 m，炸药所处水深为34.8 m，如图4所示。

通过计算机模拟仿真计算，得到舰船遭受水下非接触爆炸时的舰船结构损伤情况，如图5所示。从仿真结果可知，舰船在遭受爆炸后结构损伤严重并丧失部分功能，根据3.2节中损伤等级评估标准判定舰船损伤等级处于S3和S4之间，比较可知文中方法判定结果和仿真模拟结果相吻合。

通过上述分析和2 500 t水面舰船遭受水下非接触爆炸实例，可得到以下几点结论:

1）冲击因子KSF可以用来描述舰艇受冲击的严重性，同样的KSF会产生不同形式的压力冲击波，但每种形式产生的能量是相等的。对于产生同样能量的爆炸，若θ是常数，炸药的重量越小，炸药距舰船的距离也越近，因此球面冲击波对船体的局部损伤是最早的。

2）气泡脉动因子BPF可以用来描述水下气泡脉动损伤的严重性。

3）舰船结构损伤程度可以通过KSF和BPF两个指标来判定，简单的计算便可知道舰船结构损伤情况，可为作战过程中水面舰船遭受水下非接触爆炸作用结构损伤状况提供预测。

［1］浦金云，金涛，邱金水，等．舰船生命力［M］．北京:国防工业出版社，2008.386－438．

PUJin-yun，JINTao，QIUJin-shui，etal．Ship survivability［M］．Beijing:National Defence and Industry Press，2008.386－438．

［2］SHIN Y S．Ship shock modeling and simulation for far-field underwater explosion［J］．Computers and Structures，2004， （82）:2211－2219．

［3］浦金云．损伤树在舰艇作战系统生命力中的应用［J］．船舶工程，2004，（1）:14－16．

PU Jin-yun．Damage tree method-survivability evaluation of naval ship combat system［J］．Ship Engineering，2004，（1）:14－16．

［4］郭镇明，唐嘉亨，丛望．非接触爆炸下舰船电力系统生命力的研究方法［J］．船舶工程，1996，（2）:31－35．

GUO Zhen-ming，TANG Jia-heng，CONG Wang．A method for estimating survivability of warship electric power system in non-contract explosion［J］．Ship Engineering，1996，（2）:31－35．

［5］BJARNHOLT G．Explosive expansion works in underwater detonations［C］．Proceedingsof6thSymposiumon Detonation．San Diego，1976.540－550．

［6］丛望，唐嘉亨，郭镇明．接触爆炸下舰船电力系统生命力的研究［J］．哈尔滨工程大学学报，1995，（2）:54－59．

CONG Wang，TANG Jia-heng，GUO Zhen-ming．A method for estimating survivability of warship electric power system in contract explosion［J］．Journal of Harbin Engineering University，1995，（2）:54－59．

［7］朱锡，张振华，刘润泉，等．水面舰艇舷侧防雷舱结构模型抗爆试验研究［J］．爆炸与冲击，2004，（2）:133－139．

ZHU Xi，ZHANG Zhen-hua，LIU Run-quan，et al．Experimental study on explosion resistance of cabin near shipboard of surface warshipsubjectedtounderwater contact explosion［J］．Explosion and Shock Wave，2004，（2）:133－139．

［8］LIANG Cho-chung，TAI Yuh-shiou．Shock responses of a surface ship subjected to non-contact underwater explosions［J］．Ocean Engineering，2006，（33）:754－772．