基于适应度函数及交叉操作改进的自适应遗传算法

□文/窦明鑫刘晓霞

（1.中国地质大学长城学院；2.河北金融学院 河北·保定）

基于适应度函数及交叉操作改进的自适应遗传算法

□文/窦明鑫1刘晓霞2

（1.中国地质大学长城学院；2.河北金融学院 河北·保定）

为了提高遗传算法的搜索效率，给出了一种改进的遗传算法。该算法改进了适应度函数和交叉操作，扩大了搜索范围。通过三个经典函数的测试表明，改进算法与基本遗传算法相比较，在函数最优值、平均收敛代数、收敛概率等方面都取得了令人满意的效果。

自适应遗传算法；适应度函数；交叉操作；实数编码

收录日期：2012年5月10日

引言

遗传算法（GA）由美国Michigan大学的Holland教授于1975年首先提出，后经De Jong、GoldBerg等人改进推广，广泛应用于各类问题。它是一种模拟自然界生物进化过程与机制的全局概率优化搜索方法。

本文对自适应算法进行了改进，构造了一种自适应的适应度函数，以便更好地进行复制、交叉、变异操作，之后对实数的交叉操作进行了改进，扩大了搜索范围，提高了算法全局搜索能力，最后利用改进算法进行仿真实验，结果表明本算法具有收敛概率高和平均收敛代数少的优点。

一、改进的遗传算法

（一）改进的适应度函数。为了使进化前期原本函数值低的个体有更大的概率被选择，保持种群多样性防止“早熟”，而在后期可以转成正常选择操作，开始局部求精的搜索。本文参考文献将适应度函数改进为：

其中，f（xi）是所对应的函数值是群体的平均函数值，fmax为上一代最优解所对应的函数值，t为当前代数，T为预先设置好的最大迭代次数。

这种调整使得原本函数值远离群体均值的个体适应度变大，使其被选择的概率增大，而对种群贡献较小的函数值处于中间位置的个体被选择的概率变小，使得在进化前期可以保证种群的多样性，避免产生模式欺骗问题或过早陷入局部收敛。

（二）改进的交叉操作。由于本文对适应度函数的调整在前期较好地保持种群的多样性，在进化前期为了提高算法的搜索效率，交叉概率设定的较小，在进化后期为了保证种群的多样性加大了交叉概率，所以本文设定Pc=0.25+0.45·，其中t和T的含义同上。

本文改进的交叉操作是先在交叉前产生三个服从均匀分布的随机数a∈（0，1）、b∈（-1，1）、c∈（-1，1），然后假设x1、x2是要交叉的两个父代，个体变量为m维，则 x1、x2可以表示成 x1=（x11，x12，…，x1m），x2=（x21，x22，…，x2m），其中 xij∈［α，β］，设定△1＝（△11，△12，…，△1m），△2＝（△21，△22，…，△2m）为位移变量，其中△ij=min｛（xij-α），（β-xij）｝（i=1，2；j＝1，2…m），最后进行两次操作得：

x1'、x2'、x1''、x2''分别为两次操作所产生的子代，从这4个子代中选取适应度大的两个保留到下一代。通过这种操作可以有效地避免两个数值相近的个体进行“近亲繁殖”（数值相近的个体若只进行（3）式的操作会导致种群多样性快速下降），同时由于 b、c 的选取，生成的 x1'、x2'是两个不相干的个体，彼此之间独立，由（3）式决定的后代还可以使子代遗传父代的某些有用因素，同时由于（2）式的位移调整，使得（3）式生成的后代比一般的算数交叉产生后代的范围得到扩大，提高算法的搜索范围，避免搜索陷入一个局部区域而出现“早熟”，最后再引入竞争机制在这四个后代中选出两个最好后代个体，这样在保证多样性的同时可以加快收敛的速度。

二、算法步骤

Step1 采用实数编码产生初始种群，在函数定义域内按照均匀分布随机产生n个个体｛xi｝（i＝1，2，…n），设定最大进化代数为T。

Step2 计算每个个体的函数值，之后计算种群函数的平均值，最后按照本文设定的适应度函数，即（1）式计算当前种群中每个个体的适应度。

Step3 根据每个个体的适应度，采用比例选择法。通过这种适应度转换，使得在进化前期原本函数值小的个体将有更大的概率被选择，保持了种群多样性。

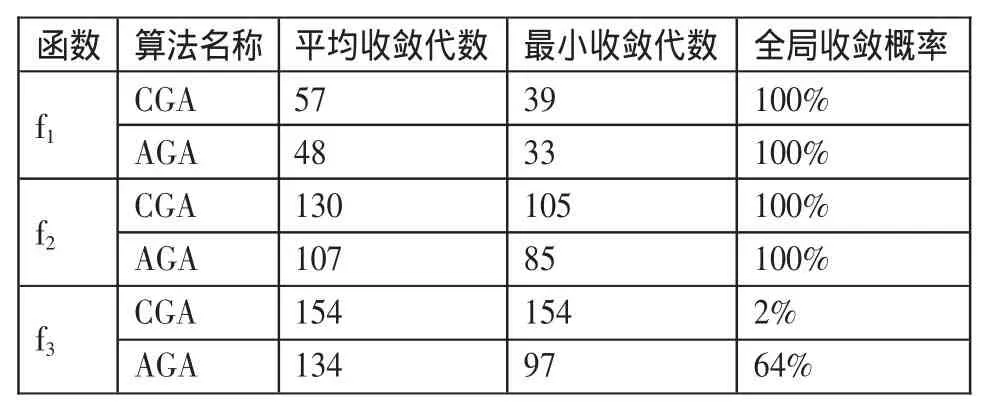
表1 三种算法对测试函数的运行结果

Step4 按照概率Pc在种群中随机选择父代个体，然后应用本文改进的交叉方式进行交叉，最后通过竞争选取两个最好的个体作为子代个体。

Step5 按照概率Pm变异操作如下：假设个体xi中第k个分量xki是待变异个体，通过高斯变异可以得到新的个体分量xiknew，其中：

Step6 最优保存策略，结合文献本文将最优保存策略算法做如下修改：第一步，计算每个个体的函数值，然后排序，找出最优解，最差解；第二步，若上一代最优解的函数值比当前最优解的函数值大，则用上一代的最优解替换当前最优解；若上一代的最优解函数值小，则用上一代的最优解替换当前中的最差解。这样基于Markov链的数学理论分析表明，保留最优个体策略的遗传算法能够以概率1收敛于最优解。

Step7 满足迭代次数即停止，否则代数加1，转入Step2。

三、仿真试验

（一）测试函数。选取参考文献的测试函数为：

其中，f1为单峰二次函数，当（x1，x2，x3）＝（0，0，0） 时有全局最小值 0；f2是一维连续且含三角函数的多峰函数，当x=1.8505时，全局最大值为 3.8503；f3是一个典型的大海捞针类函数，该函数将形成不同严重程度的GA 欺骗问题，当（x1，x2）＝（0，0）时函数有最大值3600，并且函数有4个局部极值点：（5.12，5.12），（-5.12，5.12），（-5.12，－5.12），（5.12，－5.12），函数值为 2748.78。

（二）测试结果对比分析。用本文算法同基本遗传算法进行比较，其中取种群规模m=200，基本遗传算法的交叉概率pc=0.85和变异概率pm=0.1，自适应遗传算法的交叉概率和变异概率分别为：

其中 pc1=0.85，pc2=0.65，pm1=0.15，pm2=0.05，f'为两个要交叉个体适应度大的个体适应度值，最大迭代次数设为T=200，对各测试函数分别独立运行50次得到表1。（表 1）

通过实验表明：本文的算法在对函数的测试中，达到最优值的收敛代数明显减少，得到了令人满意的效果，特别在对函数f3的测试中，本文算法不仅减少了收敛的代数，而且提高了明显算法的收敛概率。所以，本文的算法在减少收敛代数方面和提高收敛概率方面是具有优越性的。

四、结束语

本文提出改进的适应度函数，使得在进化初期一些函数值差的个体也能有更高的概率参与到选择、交叉、变异操作中，保存了种群的多样性，同时在自适应交叉的过程也采用了新的方法使得在避免“近亲繁殖”的基础上扩大了搜索范围，大大提高了算法收敛速度和收敛概率，使本文算法具有较高的计算效率。

[1]李敏强等.遗传算法的基本理论与应用[M].北京：科学出版社，2004.

[2]陈理国，蔡之华.改进的正交遗传算法及其在函数优化中的应用.计算机工程与设计，2008.29.13.

[3]杨春松，程文明.一种进化类混合算法的研究[J].计算机仿真，2007.10.10.

[4]王小平，曹立明.遗传算法——理论、应用与软件实现[M].西安：西安交通大学出版社，2002.

TP3

A