数值仿真在材料力学教学中的应用

2012-03-05蒋敏敏王惠芬肖昭然

河南建材 2012年3期

蒋敏敏王惠芬肖昭然

河南工业大学土木建筑学院（450001）

0 前言

材料力学是工科院校重要的专业基础课程，目前在材料力学的教学中存在着以下的问题:材料在外荷载作用下的基本变形形式，在横截面上的应力分布特征只能通过教师的描述，或通过材料力学试验结果的反分析，推算出可能存在的横截面应力状态，部分学生理解起来存在一定的困难。将有限元数值仿真应用于材料力学基本变形的分析中，使得学生能够直观观察到构件的应力分布特征，能够更形象生动地理解材料力学相关理论。

1 数值仿真在材料力学教学中的优点

材料力学的基本变形有如下假设[1,2]:拉压基本变形假定纵向由许多纤维组成，拉压后纤维均匀伸长或缩短变形；扭转基本变形假设圆轴扭转由很多圆盘组成，扭矩作用下圆盘仅发生转动，圆盘间距没有发生变化；弯曲假定在中性层的纤维不发生变形，凸侧纤维发生伸长，凹侧纤维发生缩短。这些假设比较抽象，学生理解起来相对较困难。

在教学过程中如果通过建立虚拟数值模型，并分析杆件的基本变形特性，将能够更好地帮助学生深入理解材料力学基本原理。一方面，通过数值仿真建立模型,可以提高学生学习力学课程的兴趣，拓展学生的知识面。另一方面，通过数值仿真的矢量结果、云图结果等直观的表示形式，学生将能够深刻地理解构件受力变形的基本特性。

2 数值仿真在教学中的应用

以ABAQUS有限元软件为工具[3]，以材料力学中拉压、扭转和弯曲等几种基本变形形式为例,建立的数值仿真模型，模拟低碳钢材料在不同荷载作用下的受力变形特征。

2.1 拉压基本变形形式

主要模拟各种基本变形的构件在弹性阶段的变形特征,因此材料参数选为:弹性模量E=200 GPa，泊松比ν=0.3。模拟拉压杆件的模型为横截面边长为0.2 m正方形，长度为1 m的受压缩杆件，压缩荷载的大小为1 MN。计算中划分的单元为正方体，大小为0.05m。计算结果如图1所示，图中表示了杆件内应力的矢量分布，从数值计算结果可见，整个压缩杆件内受到的均为压缩应力，且整个横截面内应力为均匀分布。

2.2 扭转基本变形

扭转基本变形模拟的是直径为0.2 m,长度为1.0m的等直圆杆,在大小为10 kN·m的外力偶矩作用下的问题。计算模型在圆轴的径向划分等厚度的6层单元，沿着杆件轴线方向单元的长度为0.05 m。在外力偶矩的作用下，圆轴横截面的应力分布如图2所示，横截面上应力方向垂直于半径方向，且大小与到圆心的距离呈正比的关系。

2.3 弯曲基本变形

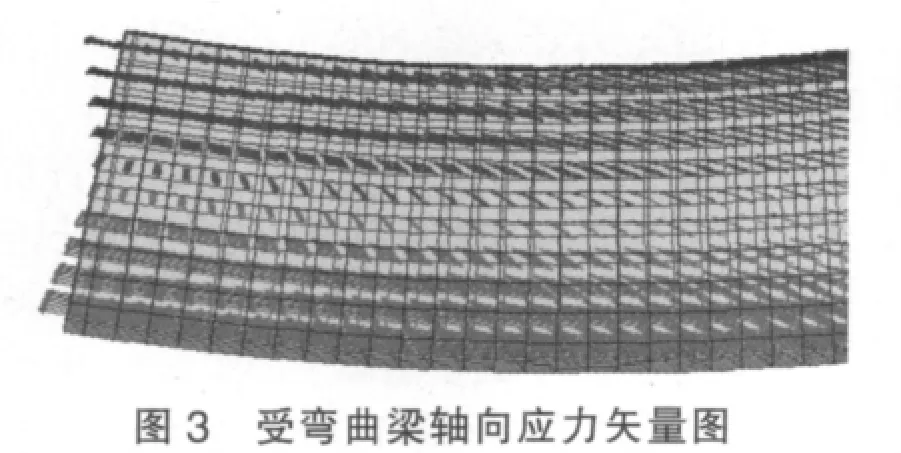
弯曲基本变形数值模型模拟的为一外伸梁的受力特性，梁横截面为边长0.1m的正方形，梁总长度为1.2 m，在靠近梁两端的位置设支座，约束梁y方向的位移,同时在两侧靠近支座位置施加25 kN的y方向荷载,单元划分为边长0.01 m的正方体。集中荷载之间的梁段为纯弯曲的梁段，纯弯曲梁段轴线z方向的应力矢量图如图3所示。从计算结果可见,受纯弯曲梁应力的方向为沿着轴向方向，存在中性轴层，轴向应力为零，梁底端为受拉部分，顶端为受压部分，距离中性轴越远，应力呈线性增大。