明渠急流分流结构数值模拟

燕春林 何孟狄 余 振 汪德金

（中国市政工程西南设计研究总院 四川 成都 610082）

河道或渠道采取分流措施已广泛的应用于各种水利工程中，诸如河道防洪、城市防洪、农业灌溉等方面。明渠分流常见布置是在明渠侧墙部位设置分流渠道，具体体型则由实际效用决定。在明渠分流处，存在有一定的流线分离，从而出现局部回流区和束窄现象。Neary and Odgaard研究了低佛汝德数时非等宽明渠直交分流区的流场结构、分流能力和分流点处的水深。A.S.Ramamurthy等[2]和Jianchun Huang等[3]采用数值模拟研究了分流渠和主渠交角为90°时的分流区的流场结构。Bahareh Pirzadeh,Hamid Shamloo采用二维和三维数值模拟相结合的手段，模拟了分流明渠的水流结构。Amruthur S.Ramamurthy[5]等采用试验研究了分流明渠流态和分流渠进口上游主渠进佛汝德数对分流量的影响。

以上研究的分流明渠底板坡度变化较小，分流渠和主渠坡度基本相同，仅对不同分流渠角度的流场和分流量等水力特性指标进行了详细研究。本文以分流渠与主渠交角为40°，且分流渠底板为急流底坡的三维异型分流结构。

研究对象，并将数值模拟结果与模型试验结果相比较以验证数值模拟的有效性。

1 计算模型及边界条件

1.1 数学模型和计算方法

本文采用引入具有自由面追踪功能的VOF法和标准kε双方程模型来对中闸室出口空腔进行数值模拟，其基本方程为：

式中：ρ和μ分别为密度和粘性系数，其表达式为：ρ＝αwρw＋（1－αw）ρa，μ＝αwμw＋（1－αw）μa，其中，αw为网格上水的体积分数，0≤αw≤1，ρw、μw和ρa、μa分别指水和空气的密度、粘性系数；p为修正的压力；μt为紊流粘性系数，可由紊动能k和紊动耗散率ε求出其中，Cμ为经验常数，fi为流体受到的惯性力，本文仅有重力。σk和σε分别为k和ε的紊流普朗特数，以上各式中的常数取值见表1。

表1 控制方程中的常数值Table1 The constant value of control equation

方程离散采用有限体积法，对流项采用二阶迎风格式，扩散项采用中心差分格式，压力速度耦合采用PISO算法。每个网格上的体积分数变化采用求解下式完成：

其中，t为时间，ui和 xi分别为速度分量和坐标分量。

1.2 边界条件

数值模拟体型如图1所示，由主管道、分流结构、分流管道和主渠收缩段组成。分流结构分为分流中墩、1#分流道和2#分流道分流管道。分流结构进口处设分流墩，其前沿导向角（前沿尖角射线与主渠轴线的夹角）为40°，分流墩段底板为三维异型结构，由多段弧组成。基本参数为：主渠道横断面为3.1×2.9m （宽×高），长33m；1#分流管道进口横断面为5.42×4m （宽×高）；2#分流管道进口横断面为5.17×4m （宽×高）；主管道束窄处断面为1.3×4m（宽×高）；分流管下游主管道典型横断面为4.0×4.0m（宽×高），长41.5m。该结构的主要特点是：分流结构进口不是简单设置于主渠侧墙处，而是将进口设置于主渠内并与主渠收缩段相结合，分流渠底板坡降较大，使水流呈急流形式，以达到增加分流能力的目的。网格划分采用全局非结构化网格，最小计算尺寸为0.1m。进口采用速度边界条件，空气进口和出口均采用压力边界条件，固壁采用无滑移边界条件，粘性底层采用标准壁面函数法处理。

1.3 计算工况

根据模型试验结果，并与模型试验相对应，其数值模拟的计算工况如表2所示。

图1 计算体型Fig.1 Numerical modle

表2 数值模拟工况Table2 Performance of numerical simulation

2 成果分析

2.1 流态及流场分布

数值模拟结果表明：各计算工况下，该体型参数均能满足泄流能力，管道内流态基本稳定，随着流量增加，1#和2#分流道内部沿侧壁有翻转水流，分流墩下游局部有较大水跃，紊流程度剧烈，主渠收缩段后有水力坡降会陡增。当流量小于20m3/s时，管道内水流平顺，分流墩后主渠收缩段对水流束窄能力较小，水流进入分流管道弯段以后，受弯道离心力作用而向外偏转，在水流进入直段前以弱水跃衔接。当流量大于30m3/s时，分流墩后主渠收缩段对水流束窄能力增强，分流管道流量相应增加，导致分流段流速增加，分流管道偏转水流和分流墩下游水跃强度均增加。当流量大于65m3/s时，分流墩后主渠收缩段对水流束窄能力明显增强，水流在分流段段进口形成回流和平面旋流，但受下游水位影响，分流墩后呈淹没水跃（图2～图4）。

图2 分流结构流态（Q=10m3/s）Fig.2 The flow pattern of diversion structure(Q=10m3/s)

图3 分流结构流态（Q=30m3/s）Fig.3 The flow pattern of diversion structure(Q=30m3/s)

图4 分流结构流态（Q=50m3/s）Fig.4 The flow pattern of diversion structure(Q=50m3/s)

2.2 水面线分布

图5 计算结果水面线（主渠）Fig.5 Water surface profile of numerical simulation

水面线分布是衡量分流结构体型是否合理的一个重要水力特性指标，通过与模型试验测量水面线相比较，从而验证数值模拟成果。在流量小于20m3/s时，主渠收缩段对水流的束窄能力有限，主渠内水面线均平顺；流量大于30m3/s后，主渠收缩段对水流的束窄能力逐渐增强，束窄断后水力坡降也逐渐增大。对于分流结构段，在流量Q≤10m3/s时，水面线分布均匀，当流量Q≥20m3/s后，因流速增大并受离心力影响而向左侧墙偏转，流道内横断面水面线分布不均匀。在流量Q≤5m3/s时，分流墩后以弱水跃衔接，当流量Q≥20m3/s后，分流墩后水跃强度逐渐增大，当流量Q≥50m3/s后，随着下游水位升高，水跃会呈淹没状态（如图5、图6）。数值模拟结果与模型试验结果对比表明，二者水面线结构符合良好（如图7、图8）

图6 计算结果水面线(分流渠)Fig.6 Water surface profile of numerical simulation

图7 计算值与模型值对比（主渠道、工况6）Fig.7 Comparison of stream line between numerical and measured(main channel,performance 6)

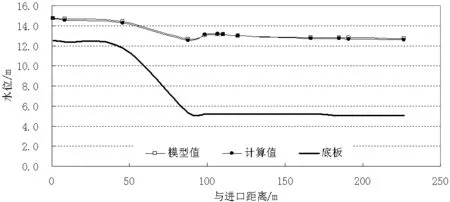
图8 计算值与模型值对比（分流管道、工况6）Fig.8 Comparison of stream line between numerical and measured(diversion channel,performance 6)

2.3 分流比

分流比是衡量分流结构分流能力大小的一个重要指标。比较分析表明，数值模拟成果与模型试验成果符合良好（如表3）。表3说明，各工况下，分流结构分流后两渠道流量比值在1.8∶1～3.3∶1之间，说明分流结构具有较强的分流能力，该体型能满足分流要求。

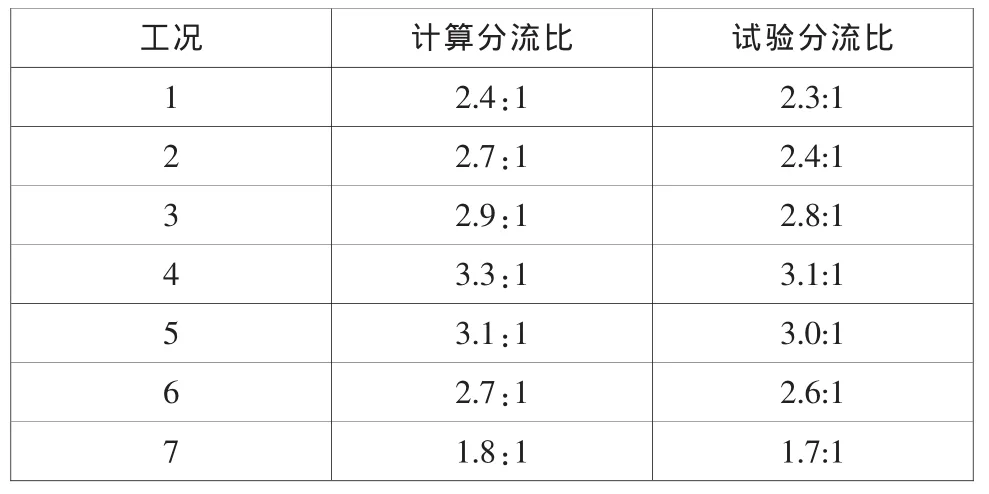
表3 各工况下的分流比（分流渠道流量：分流后主渠道流量）Table 3 The split ration under different operation condition(discharge of main channel:discharge of diversion channel)

3 结论

急流分流结构是一种较为新型的分流结构，其分流能力和分流道体型是影响水力学指标的关键因素。本文通过数值模拟模型试验研究急流分流结构并与模型试验成果相比较，二者在流场、水面线和分流比方面均具有较好的符合性，说明数值模拟结果有效。该急流分流结构能分走主渠2/3以上的流量，说明具有较强的分流能力。

［1］Neary,V.S.and Odgaard,A.J.,(1993).Three-Dimensi-onal Flow Structure at Open Channel Diversions[J].Hydr.Engrg.,ASCE,119(11)∶1223-1230

［2］A.S.Ramamurthy,Junying Qu,Diep Vo,and Chao Zhai.3-D Simulation of Dividing Flows in 90°Rectangular Closed Conduits[J].J. Fluids Eng.September 2006,128(5)∶1126-1129.

［3］Jianchun Huang,Larry J.Weber,and Yong G.Lai.Three-Dimensional Numerical Study of Flows in Ope-n-Channel Junctions[J]. J.Hydr.Engrg.2002,128(3),pp.268-280

［4］Amruthur S.Ramamurthy,Duc Minh Tran,Luis B.Carballada. Dividing Flow in Open Channels[J].Journal of Hydraulic Engineering, Vol.116,No.3,March 1990,pp.449-455.

［5］Bahareh Pirzadeh,Hamid Shamloo(2007).Numerical investigation of Velocity Field in Dividing Open-Channel Flow [A].12th WSEAS Int. Conf.on APPLIED MATHEMATICS,Cairo,Egypt,December 29-31,pp. 194-198.