真空多层绝热性能测试装置及初步实验验证
2012-02-26朱浩唯黄永华吴静怡
朱浩唯 黄永华 李 骏 吴静怡 李 鹏
(1上海交通大学制冷与低温工程研究所上海市低温技术与测试应用服务平台 上海 200240)(2上海宇航系统工程研究所 上海 201108)
1 引言
高真空多层绝热技术(MLI)[1-4]凭借其优越的绝热性能在低温液体储存领域得到了广泛应用。在考虑近地轨道推进剂长期存储技术时,由于存在现成的高真空环境,因此,使用多层绝热可有效地减少进入储箱的漏热,是低温推进剂在轨存储的理想绝热方式。鉴于发生升空过程以及在轨运行的特殊性,地面应用中常规的多层绝热材料布置方式不仅不能达到强度、重量和绝热性能等多参数最优配置水平,甚至可能无法胜任应用条件。变密度多层绝热是一种有潜力的改进技术。
多层绝热材料通常由几十层被间隔的低放射率防辐射层组成,间隔物为低热导率材料。防辐射层一般为铝箔、单层或双层镀铝的聚氨酯薄膜。间隔层则有玻璃纤维布、涤纶丝网、T型纸和P型纸等。
多层绝热系统中的热传导是复杂的,包含了辐射传热、固体导热、残余气体导热以及对流换热。很难以一个统一且精确的模型对多层绝热的传热进行计算。Krishnaprakas[5]通过对不同种配置的 MLI中热流的拟合简化了4种传热的经验模型,论证了热导率和发射率的相关性。Mikhal’chenko等人[6]对残余气体在多层绝热中对温度和压强的影响做了实验及理论阐述。Kokkolaras[7]对传热过程当中的热力学参数做了优化,并得出一套算法来计算多层绝热系统。
从已有的理论分析[4,8]可以看出,在绝热材料的高温段,辐射热流占了总热流的绝大部分;相对地,固体导热、气体导热以及气体对流则可以忽略不计。而在绝热材料的低温段,相邻防辐射屏之间的固体导热所占的比例明显增大,辐射热流所占的比重则越来越小。因此,对于一定数量的防辐射屏和间隔材料,如何选择径向(绝热材料厚度方向)的层密度分布,对于绝热层的绝热性能有很大的影响。本研究建立了一套低温用真空多层绝热材料性能测试装置,用于研究变密度多层绝热材料的特性规律。以内密外疏的层密度分布方式为例,实验研究了绝热层内的温度分布和漏热率情况,初步验证了试验系统的可行性和理论模型的正确性。
2 实验系统介绍
研究所建立的稳态液氮蒸发圆柱型量热器如图1所示,用于对高真空多层绝热材料的传热性能进行实验研究。其中,外筒体(真空壳体)采用夹层结构,夹层内布置常规多层绝热材料并抽真空至10-4Pa量级以尽量减少筒内测试系统和外界环境之间的换热。筒内的测试系统主要由上保护腔、测试腔、下保护腔和热源铝屏组成。上下保护腔内都加注液氮用来隔断测试腔在轴向的辐射换热,同时消除在该方向的边界效应。此外,控制上下保护腔的背压使其稍高于测试腔的背压以防止从测试腔蒸发的气体在穿越上保护腔的管道中冷凝,实际采用鼓泡器来控制实现。绝热层热端布置有带电加热的铝屏作为均匀的热端辐射壁(铝屏在竖直方向覆盖下保护腔、测试腔和上保护腔,避免在测试腔段发生边缘效应)。铝屏上按螺旋状缠绕有薄膜电加热带,根据需要提供所需加热功率,并在其外层粘贴铝箔胶带纸以使电加热的热量更好地传递给铝屏。实验时,首先控制铝屏温度到目标值,当整个绝热系统达到稳定状态时,根据测得的测试腔出口气体流量,可间接获得穿透测试段外侧包裹的绝热层样品的热流量,从而评价绝热系统的性能。
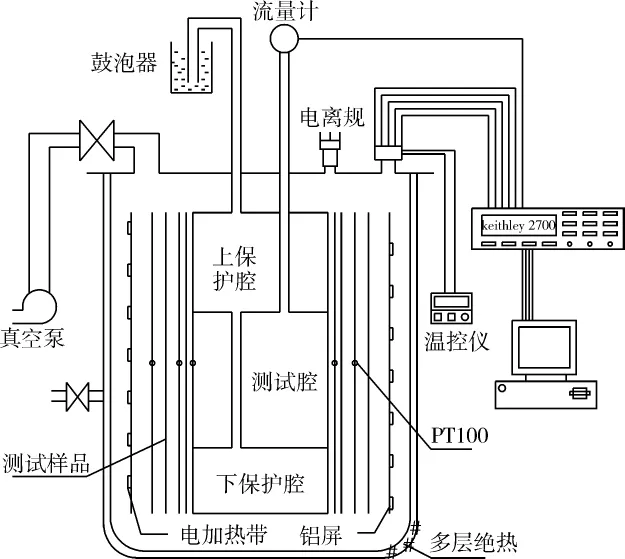
图1 实验装置结构图Fig.1 Schematic diagram of LN2boil-off apparatus
图2为整个系统的实物图。该实验系统由4部分组成:抽真空系统、测量系统、液体充注系统以及数据采集和控制系统。抽真空系统为分子泵机组,常温下将筒内的真空度提高到10-3Pa以上量级,从而消除气体导热和对流的影响。测量系统由铂电阻温度计PT100、FS4001小流量气体流量传感器以及真空电离规组成,分别用于测量绝热层内各处的温度数据、测试腔出口蒸发液氮的流量数据以及筒内的真空度。控制系统根据铝屏的温度来调节输出到薄膜电加热带的功率从而达到控制铝屏温度的目的。数据采集系统由Keithley 2700多通道数据采集仪和PC计算机组成,用来记录温度和流量的变化过程。液体充注系统用来控制保护腔和测试腔内的液氮液位,确保保护腔和测试腔始终处于较高的液位以防止由于液位过度下降而影响测试结果。
所用的多层绝热为双层镀铝的聚氨酯薄膜和T型纸间隔物组成的复合材料(双层镀铝的聚氨酯薄膜厚度为0.01 mm,T型纸薄膜厚度为0.1 mm)。在靠近冷边界处,采用1层镀铝聚氨酯薄膜和1层T型纸交错的方式缠绕多层绝热材料,共布置9层。在靠近热边界处,采用1层镀铝聚氨酯薄膜和5层T型纸交错的方式缠绕多层绝热材料,同样布置9层。在绝热层外侧进行限位,以防止绝热层在系统抽空过程中由于筒内压强的不均匀而发生层位置的变化,绝热层总厚度为12 mm。

图2 试验系统实物图Fig.2 Experimental setup under test with liquid nitrogen
在液氮充注过程中,先对上下保护腔进行液氮充注,然后对测试腔进行液氮充注,充注过程非常缓慢以防止过大热应力的产生以及温度和流量的剧烈波动。待足够长时间后绝热测试系统达到稳态,稳态漏热率可由式(1)计算(由于背压约为101.325 kPa,故认为气体处于理想气体状态):
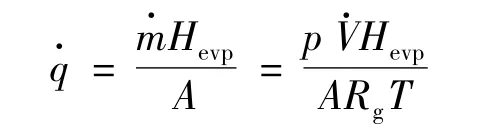
3 实验数据分析
实验过程中,依次将热端辐射背景铝屏的温度控制在35、50、65和80℃,其对应的热边界温度(即最外层防辐射层的温度)依次为279、285、293和301 K。记录绝热层内各测温点温度和测试腔出口流量的变化过程,25小时后温度变化速率达到0.001 K/min,认为已达稳定工况。同时,始终确保上保护腔有充足的液位以防止测试腔出现纵向漏热的情况。
3.1 绝热层温度分布在降温过程中的变化规律
为了解液氮充注过程中冷量在多层绝热材料内的传递规律,图3绘制了热边界温度为285 K时各层温度随时间的变化曲线(其它热端控温情况类似)。其中,各温度计位置如表1所列。其它热边界温度情况类似。

图3 绝热层降温曲线Fig.3 Cooling process within multilayer insulation

表1 各温度计在绝热层中的位置Table 1 Position of each thermometer
从图3中可以看出,绝热层需要很长的时间才进入稳定状态。刚开始冲注液氮时,由于测试装置本身的热容大,各层的温度下降得比较缓慢,之后随着液氮进一步注入,各层温度开始迅速下降。其中,越靠近冷边界温度下降得越快,越靠近热边界温度下降得越慢。约12 h后各层温度接近稳态温度,其变化趋于缓慢。最后,在18 h后基本达到稳定状态(以最后达到稳定的T7为例,从18 h至25 h共下降0.5 K)。在整个降温过程中,靠近冷边界的那一层最先达到平衡;而越远离冷边界,其达到平衡所需的时间就越长。
3.2 绝热层稳态温度分布规律的讨论与研究
根据之前的理论分析[4],内密外疏布置方式的绝热层内温度分布近似为抛物线。本实验中绝热层内的温度分布如图4所示,与理论预测曲线分布趋势吻合。以热边界温度为279 K时的温度分布为例,在靠近热边界的8.0 mm厚度中,温度下降了50 K左右,而在靠近冷边界的4.0 mm厚度中,温差则约为150 K。为了更加直观地揭示热边界温度变化给绝热层内温度分布带来的影响,图5还给出了热边界温度为285、293和301 K(分别对应铝片 50、65和80℃)时绝热层温度分布的差值(以热边界温度为279 K时的温度分布为基准):冷边界处温度梯度最大,之后随着l的增大而不断减小,并最终在热边界处达到最小。

图4 不同热辐射屏温度对应的绝热层温度分布Fig.4 Temperature distribution at different warm boundary temperatures
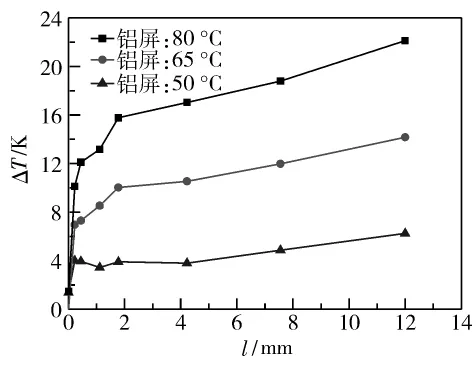
图5 铝屏温度升高时绝热层内部各温度变化Fig.5 Temperature increments within the multilayer insulation
图6给出了热边界温度为301.64 K时,实测绝热层温度分布与理论计算值[4]的比较情况。对比两条曲线可以发现,两者趋势一致,在热边界附近吻合极好;而在冷边界处,两条曲线出现比较大的偏差:理论曲线温度明显低于实验曲线,且其分布曲线趋近于一条直线,而实验曲线的斜率则有一个从大到小的渐变过程。此外,在层密度变化的交界处,理论曲线的温度斜率有明显的变化,而实验曲线在该交界处的过渡则比较光滑。造成这种差别的原因主要有两个方面:一是间隔材料的热导率实际会随着温度的下降而减小;二是由于冷边界处间隔材料会受冷收缩,导致间隔材料纤维之间以及相邻两层间隔材料之间的接触面积减小,使得接触热阻变大(等效于间隔材料的导热率进一步减小)。而在先前的理论计算中,没有考虑这两种变化所产生的影响,使得冷边界处的理论温度分布曲线偏离实验曲线。针对间隔材料等效热导率随温度下降而显著减小的规律,将原迭代计算中使用的间隔材料热导率进行了修正,其结果在图中用虚线表示。可以看到,改进之后的温度分布与实验结果非常接近。

图6 理论和实验的绝热层温度分布Fig.6 Difference between experimental and theoretical temperature distributions
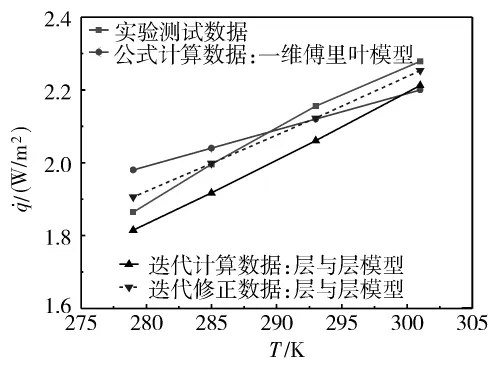
图7 热流随热边界温度的变化关系Fig.7 Heat flux vs.warm boundary temperature
3.3 热流随热边界温度的变化规律
为进一步研究这种内密外疏布置方式的绝热性能,图7列出了单位面积热流密度随热边界温度变化的实验和理论曲线,均大致呈线性关系。迭代计算(包括修正后的迭代计算)所得热流值是根据层与层模型[4]计算得到的。其中,修正后迭代法计算出热流值与实验值相当接近,且斜率也吻合。图中所谓公式计算法即通过一维傅里叶简单模型计算:
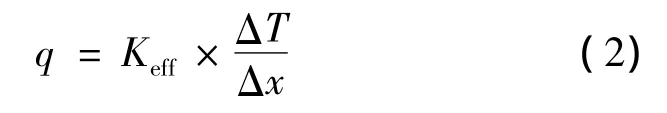
式中:Keff为复合材料的有效导热系数,其值为1.2×10-4W/(m·K)(由材料的供应商提供),Δx为绝热层的厚度,其值为0.012 m,ΔT为冷边界和热边界的温差。计算所得曲线的斜率则稍小于实验曲线的斜率。这是由于公式中所使用的材料的有效导热系数是假设为标准布置方式(一层防辐射屏夹一层间隔材料)的单一导热系数,与本实验中所使用的布置方式有所区别。即同样的厚度中,采用本实验中的层密度布置方式所包含的防辐射屏数比采用标准布置方式所得到的防辐射屏数更少。
4 结论
通过对采用内密外疏方式布置的多层绝热材料的实验测量,验证了实验装置的可行性。发现在沿绝热层厚度方向靠近热边界的很大范围内,温度都比较平缓且大致呈线性关系;而在靠近冷边界的小厚度范围内,存在极大的温差,冷边界处1/6厚度的绝热材料承担了绝热功能的75%。同时,这种趋势会随着热边界温度的升高而变得越发明显。这与理论预测结论一致。实验结果促进了对多层材料热导率随温度的变化关系的考虑,使得进行热导率修正之后的层与层模型可更好地用于指导层密度的优化设计。
1 Bapat S L,Narayankhedkar K G.Lukose T P.Performance prediction of multilayer insulation[J].Cryogenics,1990,30(8):700-710.
2 Bapat S L,Narayankhedkar K G.,Lukose T P.Experimental investigations of multilayer insulation[J].Cryogenics,1990,30(8):711-719.
3 Jacob S,Kasthurirengan S,Karunanithi R.Investigations into the thermal performance of multilayer insulation(300-77K).Part 2:Thermal analysis[J].Cryogenics,1992,32(12):1147-1153.
4 朱浩唯,黄永华,许奕辉,等.变密度多层绝热的理论分析[J].低温工程,2011(6):42-46.
5 Krishnaprakas C K,Badari N K Dutta.Heat transfer correlations for multilayer insulation systems[J].Cryogenics,2000,40(7):431-435.
6 Mikhal'chenko R S,Gerzhin A G.,Arkhipov V T,et al.Heat transport by residual gases in multilayer vacuum insulation[J].Journal of Engineering Physics and Thermophysics,1968,14(1):80-84.
7 Kokkolaras M,Audet C,Dennis J E.Mixed variable optimization of the number and composition of heat intercepts in a thermal insulation system[J].Optimization and Engineering,2001,2(1):5-29.
8 Hastings L J,Hedayat A,Brown T M.Analytical Modeling and Test Correlation of Variable Density Multilayer Insulation for Cryogenic Storage[R].NASA report 213175,2004.
