基于多项式Wigner-Ville分布的膛内弹丸回波信号处理

杨 健，陈 曦，李学连

(1.中国人民解放军73691部队，南京 210014;2.南京理工大学电子工程与光电技术学院，南京 210094)

弹丸膛内运动参数是设计武器并对其进行改进的重要依据。在弹丸试射试验中，需要测量多个物理量来反映弹丸在膛内的运动过程，对弹丸膛内运动速度的连续测定是其中的重要环节。膛内弹丸测速主要使用多普勒测速法。弹丸在膛内做变加速直线运动，回波信号为一非平稳随机信号。弹丸的运动特征表征为回波信号的相位函数，一次相位函数表明弹丸做匀速运动，二次相位函数表明弹丸做匀加速运动，三次相位函数表明弹丸加速度变换率是常数，四次及更高次相位函数表明弹丸做变加速运动。实验表明，弹丸在膛内做变加速运动，根据Stone-Weierstrass理论，闭区间上的任意连续函数可用多项式逼近，采用多项式拟合的方法可以近似拟合弹丸膛内运动曲线。由于弹丸速度的变化与回波信号的多普勒频率之间呈线性关系，故回波信号可近似为多项式相位信号(polynomial phase signal，PPS)。

对PPS信号的分析和处理是目前信号处理领域的热点，现有的PPS信号分析方法可以分为参数化方法和非参数化方法。参数化方法利用信号时变相位的多项式结构估计相位参数;非参数化方法以时频分析技术为代表，利用时频分布中的能量峰值得到低方差的瞬时频率(instantaneous frequency，IF)估计。通常可以利用多项式相位变换、高阶模糊度函数、多项式 Wigner-Ville分布(polynomial Wigner-Ville distribution，PWVD)等方法对PPS信号进行分析。多项式相位变换和高阶模糊度函数存在对噪声比较敏感、交叉项干扰严重等问题。PWVD是一种非线性时频分析方法，具有较高的时频聚集性，对交叉项干扰有着较好的抑制效果。文献［2］将PWVD分解为一系列 Wigner-Ville分布和 L-Wigner-Ville分布的卷积;文献［3］将PWVD与短时Fourier变换的结果按照“与”和“滤波”的方式相综合，均得到了多项式相位信号的时频分布，但算法较复杂。

1 多项式Wigner-Ville分布

1.1 信号模型

采用多项式拟合的方法对膛内弹丸速度曲线进行逼近，膛内弹丸运动过程为变加速运动，需要采用p≥4阶的多项式近似，取 p=4，5，6，7 时，误差 σ2分别为 139.86、56.95、6.76、5.83。可见，随着p的增大误差 σ2下降，当 p≥6时误差已经符合要求。虽然误差随p的增大而减小，但p增大的同时算法复杂度也呈级数提高，故采用p=6阶的多项式拟合弹丸速度曲线较合理。弹丸速度表示为

式中:ai为多项式系数。

设发射信号为

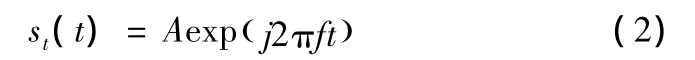
式中:A为信号幅度;f为发射频率。则回波信号为

式中:k为回波信号衰减系数;tr为时延，有

式中:R为弹丸与发射源之间初始距离。

信号的IF定义为

联立式(1)、式(3)和式(4)，可得到弹丸回波信号

代入式(5)可得到信号的IF

1.2 Wigner-Ville分布及交叉项干扰

信号sr(t)的瞬时相关函数为

对kz(t，τ)做延时τ的Fourier变换即得到信号sr(t)的Wigner-Ville分布(Wigner-Ville distribution，WVD)。对弹丸回波信号做WVD如图1(a)所示，在每个采样时间上提取峰值形成“脊线”如图1(b)所示，由于交叉项的干扰，红圈部分提取的“脊线”为交叉项干扰而非IF，造成较大误差。

图1 弹丸回波信号的WVD

针对交叉项干扰，Choi和 Williams于1989年提出了Choi-Williams分布，L.Cohen于1989年将各种改进的WVD核函数的方法统一为Cohen类时频分布。根据要处理信号的不同选用不同的核函数，核函数的性质决定了时频分布的特征［4］。1994年，R˙G Baraniuk和 D˙L˙Jones提出了基于自适应径向高斯核函数的时频分析方法［5］。1995年，B˙ Ristic等提出了基于Radon-Ambiguity变换的多分量线性调频信号的自适应双线性时频分布［6］。以上方法可以改善时频分布的聚集性和减小交叉项，但算法较复杂，对高阶PPS信号产生的交叉项干扰仍无法有效抑制。

1.3 多项式Wigner-Ville分布

1994年，B.Boashash B等人提出了多项式 Wigner-Ville分布(PWVD)，利用高阶差分方法，将PPS信号变换为复指数信号，其频率变化规律反映信号的瞬时频率，然后通过Fourier变换将复指数信号转变为沿信号瞬时频率轨迹的函数［7］。

PWVD定义为

满足方程组(10)的dl取值有很多，文献［7］给出系数为d1=d2=0.675，d3= －0.85，文献［8］给出系数为 d1=0.62，d2=0.75，d3=－0.87，采用这2种系数构造PWVD是传统选择。计算PWVD前需要对PPS信号做N倍内插，采用文献［8］、［9］的系数，符合条件的N值很大;同时计算PWVD时需要对信号进行抽取，抽取是非均匀的，由于插值倍数N较大，抽取数据占采样数据比例很小，其他无用数据占用大量系统资源。这种算法复杂度高，效率低，本文设计PWVD系数如下

将文献［7］系数、文献［8］系数、式(11)系数分别代入方程组(10)，得到 d31+d32+d33的值分别为 0.001、0.001 7、－0.001，可见式(11)的系数设计求解系数方程组得到的误差与文献［7］相等，比文献［8］小。不难看出，采用式(11)的系数，对PPS进行N=10倍内插即可。本文通过对PPS信号的10倍频完成内插，计算PWVD时，需要进行抽取，将抽取间隔增大为原来的10倍以保持结果的一致，这时PWVD的核函数被改写为

2 算法仿真结果及性能分析

采用式(11)的系数设计对弹丸回波信号做PWVD如图2(a)所示，可见完全消除了交叉项干扰，提取“脊线”如图2(b)所示，图1(b)中红圈部分“脊线”提取为信号IF。

仿真中，发射源载波频率fc=200 MHz，采样率fs=10 kHz，设定信噪比SNR=10 dB。下面对WVD、文献［7］系数的PWVD、文献［8］系数的PWVD、采用本文式(11)系数计算的PWVD的性能进行比较。首先对计算时间进行比较，考虑频率分辨率 N=64，128，…，1 024，分别进行100次试验，对试验结果取均值，比较计算时间如图3所示。当N取典型值512时，本文系数的 PWVD计算时间为0.086 4 s，文献［7］系数的 PWVD 为0.855 2 s，文 献［8］系 数 的 PWVD 为1.120 2 s，WVD 为0.023 4 s，整体来说 PWVD 的计算较WVD的计算复杂，采用本文系数的PWVD与另2种系数的PWVD相比，计算效率提高了10倍以上。

图2 弹丸回波信号的PWVD

比较不同信噪比条件下经时频分布提取瞬时频率与原信号瞬时频率之间的误差，考虑 SNR=0，2，4，…，20 dB，分别进行100次独立试验，取100次结果的均值，比较如图4所示，文献［7］系数的PWVD与本文系数的PWVD的误差曲线基本重合，图中没有标绘。从图4(a)可以看出，与WVD相比，PWVD对噪声较敏感，当信噪比低于10 dB时，误差迅速增大，当信噪比低于6 dB时，信号的时频分布峰值已无法辨认。当信噪比取典型值SNR=10 dB时，本文系数的PWVD误差为8.98，文献［7］系数的 PWVD 为 9.12，文献［8］系数的 PWVD 为46.25，WVD 为52.55。从图 4(b)可以看出，当信噪比较高时(SNR≥10 dB)，与WVD相比，PWVD可以将误差降低1个数量级左右。

图3 不同算法计算效率的比较

4 结束语

对弹丸回波信号进行分析可以得到膛内弹丸运动速度曲线，弹丸回波信号是典型的PPS信号，采用WVD分析会产生严重的交叉项干扰，造成“脊线”提取为交叉项干扰而非信号瞬时频率。本文采用PWVD分析弹丸回波信号，从仿真结果来看，有效抑制了交叉项干扰，准确提取了信号的瞬时频率。在构造PWVD核函数时，本文提出一组新的PWVD核函数系数，在处理膛内弹丸回波信号的效率、误差等方面与传统方法进行了比较，新算法将计算效率提高了10倍，误差降低了1个数量级。

图4 不同算法噪声敏感性、误差的比较

［1］ 张贤达，保铮.非平稳信号分析与处理［M］.北京:兵器工业出版社，1994:70－73.

［2］ Wang Yong，Jiang Yi-cheng.Realization of the Polynomial Wigner-Ville Distribution Based On the Convolution In Frequency Domain［J］.Journal of Electronics ＆ Information Technology，2008，30(2):286 －289.

［3］ Guo Han-wei，Wang Yan，Liang Dian-nong.Polynomial phase signal detection by different time frequency method synthesis［J］.Systems Engineering and Electronics，2004，26(4):482－484.

［4］ 吕金飞，袁嗣杰，范少龙，等.基于时频分析的高动态多目标识别与仿真［J］.系统仿真学报，2007(20):4840－4843.

［5］ Boashash B，Mesbah M.Time-Frequency Methodology for Newborn Electroencephalographic Seizure Detection［J］.The electrical engineering and applied signal processing series，2011，9(11):339 －369.

［6］ 谭小刚，魏平，李立萍.利用迭代滤波改进乘积高阶模糊函数［J］.电子科技大学学报，2009(2):182－185.

［7］ 成志峰，宋耀良，是湘全.基于高阶WVD的雷达目标回波信号处理［J］.南京理工大学学报，1999，23(2):137－144.

［8］ 刘清成，李兴国，万援;近程毫米波多普勒目标模拟器的建模与仿真［J］.系统仿真学报，2009(16):4954－4957.

［9］ John M O，Boashash B，Mesbah M.A New Discrete Analytic Signal for Reducing Aliasing in the Discrete Wigner-Ville Distribution［J］.IEEE Trans on Signal Processing，2008，56(11):5427－5434.

(责任编辑鲁 进)