半球头模型空化流场非定常特性的数值模拟

王柏秋，王聪，黄海龙，董磊，张嘉钟

(1.哈尔滨工业大学 航天学院，黑龙江 哈尔滨150001;2.北京宇航系统工程研究所，北京100076;3.哈尔滨工业大学 土木学院，黑龙江 哈尔滨150090;4.中国船舶重工集团公司第703 研究所，黑龙江 哈尔滨150036)

0 引言

空化现象具有强烈的非定常性，数值方法研究空化流场的特性时，需要针对各自特点，采用相应理论下的空化模型。不同的数学处理方法衍生出了不同的空化模型:基于空化流场连续性方程的空化模型，例如Singhal［1］模型，Zwart［2］模型;基于经验得出的空化模型，例如Kunz［3］模型，Merkle［4］模型;通过空泡受力分析得出的空化模型，例如Tamura［5］模型。

以上各种空化模型在表达空化相变率时，各有特点，其中，Singhal 模型是在不可压缩连续性方程中导出了气液两相间的质量交换率，属于直接方法，但是由于空泡动力学模型理论不完备，因此，在Singhal 模型的最后阶段的处理过程中，引入了简化的Rayleigh-Plesset 方程;Zwart 空化模型在相变率的推导上与Singhal 模型类似，但是在最后表达空泡界面运动速度时，同样引入了简化的Rayleigh-Plesset 方程;Merkle 模型是基于经验，认为空化相变率与流体密度成比例;Kunz 模型继承了Merkle 模型中的成比例的思想，在变形后的多相流方程中，采用与流体密度成比例的方法得到了空化相变率的经验表达式;Tamura 空化模型是直接对空泡进行受力分析的基础上得出的。

由以上分析可知，各种空化模型都有各自的数学方法上的优点，但各种空化模型并未有效区分空化现象中的相变过程，使得各自模型系数带宽差异较大，难于确定与空化数之间的关系，因而只能有效捕捉到空化现象中的主空泡，对一些由主空泡内气体泄漏或者其他原因产生的次生空泡无能为力，不能很好地捕捉空化流场的非定常细节。

本文基于Rayleigh-Plesset 空泡运动方程，在考虑了空泡界面上的相变作用后，导出了一个新的空化模型。针对半球头模型的空化流场进行了模型系数的数值标定，进而成功模拟了空化流场中的主空泡、次生空泡和尾空泡。与实验现象相比，所得空化流场更加真实，能够反映空化流场的非定常特性。新空化模型的导出与应用，为进一步研究空化机理提供了一定理论依据。

1 空化相变率

用R 表示发生相变时的空化相变率，则欧拉法描述有质量交换的两相流体运动的连续性方程为

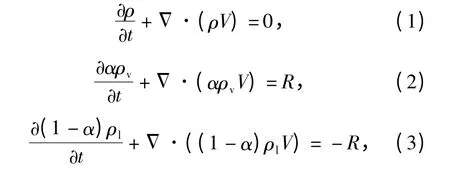
式中:α 为水蒸气体积分数;ρ 表示混合物密度，ρ =αρv+(1 -α)ρl;ρv表示水蒸气密度;ρl表示液体密度。

将(2)式进行变形，并将(1)式代入(2)式可得

不可压缩时，混合物密度变化如下

假定空泡以球形形式在液体中均匀分布，则

式中:n 表示液体中空化核数密度;r 表示球形空泡的半径。

对(6)式进行全微分可得

将(5)式和(7)式代入(4)式:

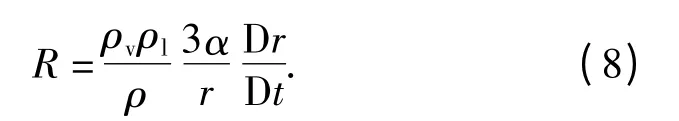
由于空泡的收缩与扩张速度极快，因此可认为在空泡变形过程中，泡内气体经历绝热过程。

当空泡扩张时，泡内水蒸气绝热膨胀，温度下降，其饱和蒸气压快速下降，使泡内气体始终处于过饱和状态，因而不断发生冷凝相变。此时，(8)式代表冷凝率，其中，混合物密度为相变后水的密度，且由于发生了相变，因而α= -1.于是，冷凝相变率为

同理，当空泡在收缩时，空泡内水蒸气同样经历绝热过程，温度迅速上升，泡内饱和蒸气压同时快速上升，使泡内气体始终处于欠饱和状态，因而，不断产生蒸发相变。此时，(8)式代表蒸发率，其中，混合物密度为相变后的水蒸气的密度，且由于发生了相变，因而α= -1.因此，由(8)式可得蒸发相变率为

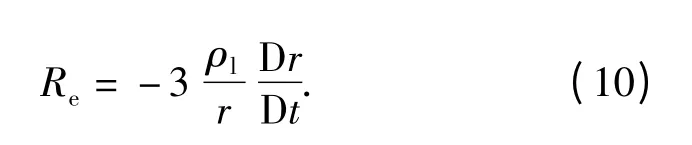
以上各式中:Re表示蒸发相变率;Rc表示凝结相变率。(9)式、(10)式即为发生空化相变时的两相之间的质量传递率。

2 空化模型

为确定以上两式中的空泡半径和空泡泡壁运动速率，考虑不可压缩流体中球形空泡运动方程，Rayleigh-Plesset 方程［6］:

式中:Σ 表示表面张力系数;νl表示液体运动粘性系数;p∞表示无穷远压力;pB表示空泡内气体压力。(11)式中，用符号头上一点表示该物理量对时间的一次导数。

忽略空泡的二阶运动影响，不计表面张力和粘性力影响时，由(11)式可得空泡泡壁运动速率为

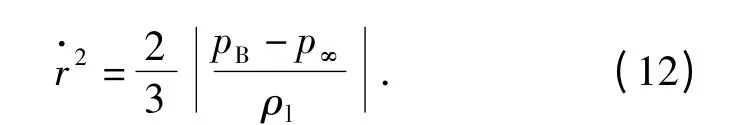
对于相变率中的空泡半径，存在众多不同的处理方式，其中，Zwart 等［2］取rB=1 μm;Martynov 等［7］将空泡半径等效成空泡长度尺度，并通过空泡核数密度来表达;Hosangadi 等［8］的可压缩空化模型和Kunz 等［3］的空化模型中，不曾出现空泡半径或者空泡尺度，而是以时间尺度的形式来衡量相间质量交换;Singhal 等［1］，张瑶等［9］通过引入经验表达式的方式定义了空泡半径。Singhal 等建议用下列半径表达式:

式中:We 表示韦伯数;vrel表示空泡流场中的特征速度。

本文拟采用Singhal 方法表达空泡半径。综合(9)式～(13)式可得相变率如下

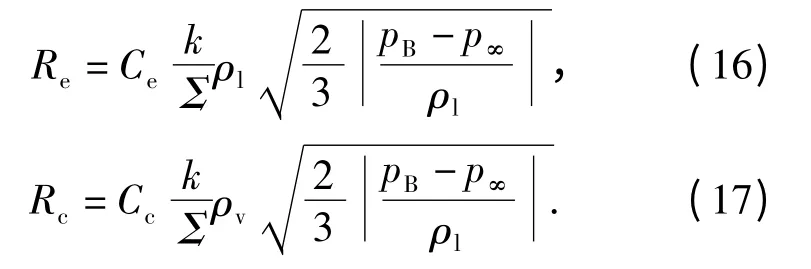
式中:Ce和Cc为综合了其他各种未知因素时的模型系数;Ce表示蒸发系数;Cc表示冷凝系数。

至此，(16)式和(17)式表达了考虑相变作用时的相变率，即空化模型。

由于水中气核的含量对空化过程有着重要影响，在标准状态下，饱和水中的非凝性气体含量约为15 ×10-6［10-12］，因此，本文取fg=1.5 ×10-5.

3 新空化模型的应用

下面利用(16)式和(17)式对半球头模型的空化流场进行二维轴对称数值计算，流场的运动方程为v∞雷诺时均化N-S 方程，数值计算模型及网格划分如图1所示，其中，模型直径为D，模型长度为L.

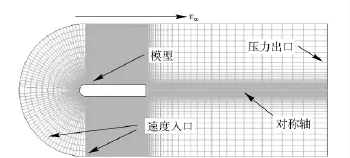
图1 模型边界条件及其网格划分Fig.1 Boundary conditions and mesh

3.1 数值方法及边界条件

根据图1所示的数值模型的特点，计算域左侧边界和两侧边界采用流向出口方向的速度入口，其中，左侧流场边界与模型前端距离为5D，流场两侧边界与模型轴线距离为5D;流场右侧边界为压力出口，与模型尾部距离为20D;计算域中间为对称轴。

边界条件中，由于流场的环境压力不变，因此速度入口按下面的空化数相似准则确定，

式中:σ 表示空化数;u∞表示入口来流速度;pv表示当地液体温度下的饱和蒸气压。

采用有限体积法对流场进行空间离散。采用PISO 算法对压力和速度场解耦。采用标准壁面函数，配合Realizable k-ε 模型模拟湍流项。

3.2 空泡形态对比分析

为与实际现象进行对比分析，在哈尔滨工业大学空泡水洞中进行了空泡实验，实验结果如图2所示。实验水洞为闭式循环水洞，工作段直径0.2 m，工作压力为常压，采用变频控制，电动机转速变化在±1 r/min，保证了工作段流场稳定。

由于空泡的不断泄气和再生，使得空化流场具有强烈的非定常性，因此在同一空化数下，拍摄了不同时刻的自然空泡形态进行对比。图2中，模型直径D=0.04 m，空化数σ=0.52，高速摄像机拍摄帧率为2 000 fps.

对比图2中同一空化数下不同时刻的空泡实验照片可见，由于非定常性及空泡泄气和不断的溃灭再生，空泡水洞实验中产生的空泡分为3 种类型，分别为位于模型前段的主空泡，如图2(a);位于模型后段与主空泡紧挨的次生空泡，如图2(b);位于模型后面的尾空泡，如图2(c).

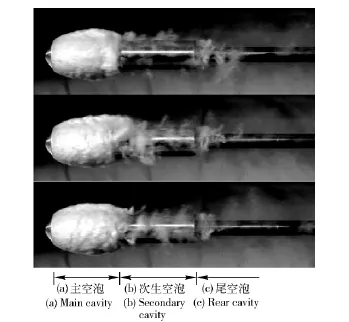
图2 空泡流实验(σ=0.52)Fig.2 Cavitating flow (σ=0.52)

由实验过程可知，流场中的次生空泡是由主空泡的不断泄气而产生的，因而其空间分布不规则，是空化流场具有强烈非定常性的重要来源之一，同时，次生空泡的存在给数值模拟工作带来了难度。

图3为半球头模型空化流场的定常状态数值模拟结果，其中，图3(a)为新空化模型计算结果，图3(b)为Singhal 模型在默认模型系数下的计算结果，图中水蒸气体积分数取值范围0～1.

与图2中的实验现象进行对比可知，图3(a)中，应用新空化模型所得到的计算结果能够同时得到主空泡、次生空泡和尾空泡，与实验现象更为接近，更能真实反映空泡流场的细节。而图3(b)所示的Singhal 模型的计算结果中，次生空泡几乎不出现，且尾空泡流场也较弱，与实验现象存在明显差异。

另外，在进行减压空泡实验时，水洞扩张段内会不断传出强烈的爆裂噪声，这正是由于减压条件增强了流场内的次生空泡的输运，使大量的次生空泡延迟至水洞扩张段内才发生不断溃灭。而常压和增压实验时，次生空泡的输运受到抑制而提前溃灭，因而，水洞扩张段内几乎无爆裂噪声。

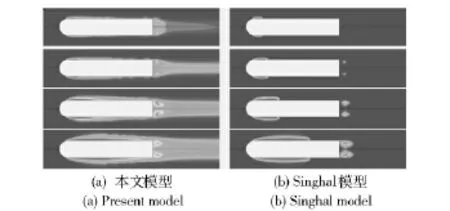
图3 不同空化数下的空泡形态对比(从上至下，空化数σ 分别为0.5、0.4、0.3、0.2)Fig.3 Cavity shape at different cavitation number (from top to down:σ=0.5，σ=0.4，σ=0.3，σ=0.2)

3.3 非定常计算结果分析

实验数据一般反应的是试验点上的某物理量在一个时间片段内的平均值，因此，为定量验证新空化模型的正确性和有效性，有必要取非定常数值计算结果的平均值与实验结果进行对比分析。

下面以图1所示数值模型为例进行非定常数值计算，模型尺寸和数值实验点的分布情况如图4所示，其中实验点的布置参照了文献［1］和文献［8］.

图4 数值实验点Fig.4 Numerical experiment points

由于次生空化区内的模型表面压力波动明显，具有特征意义，因此，图5对次生空化区内任意一点的表面压力系数随时间的波动情况进行了研究。图6是图5所示的数值计算结果的时均值与文献［8］的对比。其中，L/D 代表用模型直径D 无量纲化的模型沿程长度，表面压力系数的定义为

图5和图6的数值计算结果表明，应用新空化模型所得到的表面压力系数的时均值与文献［8］中的实验结果非常接近，证明了新空化模型对空化流场的定量计算是正确有效的。

3.4 定常计算结果分析

图7与图8分别为模型表面压力系数分布的定常计算结果与文献［8］的对比情况(σ=0.4 和σ=0.2).

在图7与图8中，表面压力系数曲线下降时，流体局部压力降低，空泡开始生成和扩张，表面压力系数曲线上升时，流体局部压力升高，空泡开始收缩溃灭。

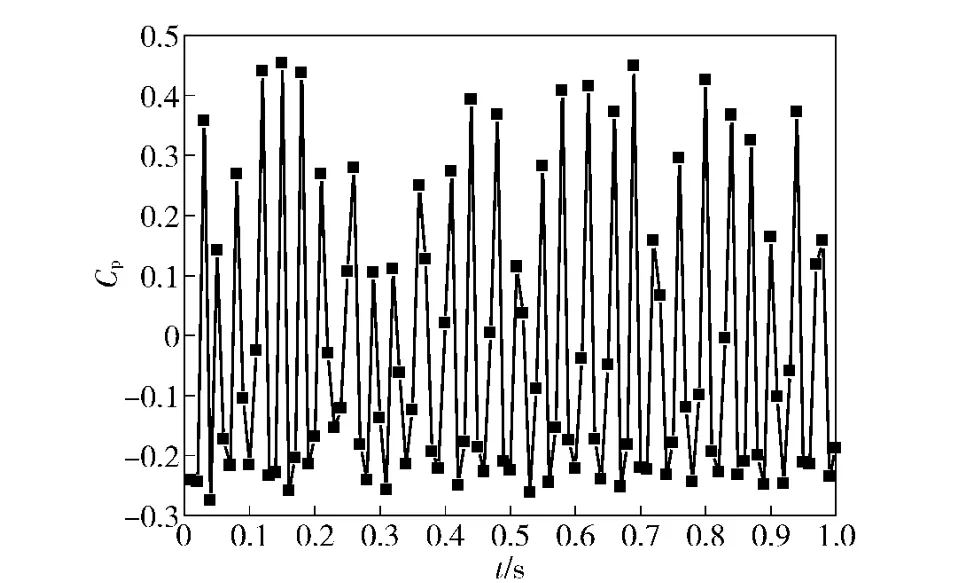
图5 P4 表面压力系数的非定常波动Fig.5 Surface pressure coefficient fluctuations of P4

图6 表面压力系数分布(σ=0.4)Fig.6 Distribution of surface pressure coefficient

由图7中表面压力系数曲线的对比可知，新空化模型计算得到的流场中，由于次生空泡的存在，使得模型表面压力系数曲线沿程波动，符合实验现象。而文献［1］的Singhal 模型计算结果中，空泡的生成与溃灭只出现了一次，没有捕捉到次生空泡，因而表面压力系数曲线平滑，没有非定常特征。

3.5 模型系数的数值标定

由(9)式与(10)式的推导及分析可知，在空泡的扩张过程中，空泡界面上发生的是冷凝现象，冷凝相变占优，而空泡在收缩时，界面上发生了蒸发现象，蒸发相变占优。因此，空化模型中的冷凝系数同时表达了空泡的扩张特性，蒸发系数同时又表达了空泡的收缩特性。由于模型中冷凝系数和蒸发系数互不相关，因此，在数值方法中，采用逐步逼近的方法对模型系数进行数值标定。通过数值模拟与文献［1，8］中的表面压力系数曲线上的主空泡位置进行比对后，针对半球头模型的空化流场，得到了如图9所示的模型系数与空化数之间的关系曲线。

图7 模型表面压力系数分布及相应空泡流场(σ=0.4)Fig.7 Surface pressure coefficient and cavity volume fraction (σ=0.4)

由图9(a)可见，模型系数与空化数关系密切，在当前空化数范围内(0.1 ＜σ ＜0.5)，随着空化数的降低，蒸发系数先减小后增加，而冷凝系数维持在较低水平，几乎保持不变。模型系数随空化数变化而变化的重要原因之一是模型自身理论不完备，例如由于缺乏空泡半径的解析表达式，因而不得不采用与以往模型类似的处理方式，即使用近似表达式来表达模型中的空泡半径。因此，在使用空化模型时，首先应确定对应空化数下的模型系数。

图10所示为使用了不适当的模型系数的计算结果。由图可见，当模型系数过大或过小时，空化流场中的相变作用增强或变弱，引起计算结果严重偏离实验，甚至可能导致流场中的次生空化消失或发生严重变形。

3.6 超空化和弱空化

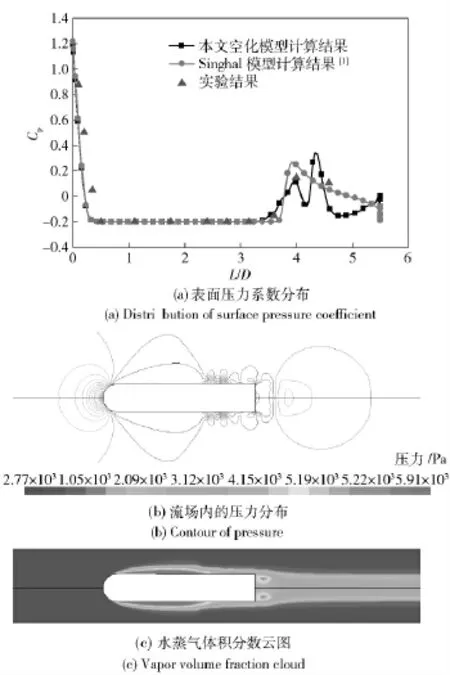
图8 模型表面压力系数分布及相应的空泡流场(σ=0.2)Fig.8 Surface pressure coefficient and cavity volume fraction (σ=0.2)

以上讨论的空化流场尚未超空化流场或者弱空化流场，例如当σ≤0.1 或σ ＞0.5.

为进一步考察模型系数与空化数之间的关系，采用同样的方法，对超空化流场和弱空化流场分别进行了数值模拟，计算结果如图11、图12 所示。

与图9的非超空化流场相比，图11 中超空化流场中的模型系数较大。由于超空泡的形成，原本附着于模型表面的次生空泡完全脱落，并与尾空泡结合形成新的尾空泡。

同时，由图11 可见，不适当的模型系数依然会导致对流场特征的捕捉失败。例如，较小的模型系数将导致流场中的尾空泡区直接消失，如图11(a)所示。较大的模型系数将导致流场发生紊乱，如图11(c)所示。

相对于超空化流场和次生空化流场，弱空化流场的模型系数与空化数之间的关系较为简单，如图12所示。图12 的弱空化流场中，没有次生空泡，甚至没有明显的空化产生，因而，模型系数不再依赖于空化数，可以自由选取。

图9 模型系数与空化数之间的关系Fig.9 Relationship of model coefficients and cavitation number

图10 不适当模型系数下的空化流场(σ=0.4)Fig.10 Cavitation flow field under improper model coefficients

至此，按照空化数的变化，空化流场可以分为3 种:超空化流，次数空化流，弱空化流。图9、图11和图12 的计算结果表明，3 种空化流场中的模型系数与空化数之间的关系有较大差别，在使用空化模型之前，应根据实验或文献资料首先对模型系数进行数值标定。

4 结论

图11 不同模型系数下的超空泡流场(σ=0.1)Fig.11 Numerical results of supercavitation flow field

图12 弱空化流场的数值模拟(σ ＞0.5)Fig.12 Numerical results of weakcavitation flow field

通过引入空泡界面上的相变作用，分析了空化流场中的相变过程。结合简化的Rayleigh-Plesset 方程，给出了一个新的空化模型。将新空化模型应用于半球头水下航行体的空化问题，得到了以下结论:

1)新空化模型的成功应用和验证表明对相变过程的分析是有效的，即冷凝发生于空泡扩张时，而蒸发发生于空泡收缩时。

2)空化流场中存在3 种典型的空泡结构，分别为主空泡、次生空泡、尾空泡。按照这3 种典型结构的空泡在空化流场中出现的可能性，空化流场亦可分为3 种类型，分别为超空化流场、次生空化流场、弱空化流场。

3)由于考虑了空泡界面上的相变作用，应用新的空化模型能够模拟主空泡、次生空泡和尾空泡，得到的计算结果更加接近实验现象。

4)模型中的相变系数不是常数，而是随着空化数改变而改变。在次生空化区内，相变系数随着空化数的减小，先减小后增加，并且，蒸发系数远大于冷凝系数。

5)空泡扩张过程中，发生冷凝相变，空泡的扩张系数又是相变中的冷凝系数;空泡收缩过程中，发生蒸发相变，空泡的收缩系数又是相变中的蒸发系数。

新空化模型物理意义明确，适用于理论分析和数值计算，为进一步研究空化机理提供了理论基础。

References)

［1］ Singhal A K，Athavale M M，LI Hui-ying，et al.Mathematical basis and validation of the full cavitation model［J］.Journal of Fluids Engineering，2002，124(3):617 -624.

［2］ Zwart P J，Gerber A G.Belamri T.A two-phase flow model for predicting cavitation dynamics［C］∥5th International Conference on Multiphase Flow.Yokohama:ICMF，2004:152.

［3］ Kunz R F，Boger D A，Stinebring D R，et al.A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction［J］.Computers ＆ Fluids，2000，29(8):849-875.

［4］ Merkle C L，Feng J，Buelow P E O.Computational modeling of the dynamics of sheet cavitation［C］∥Proceedings of Third International Symposium on Cavitation.Grenoble:［s.n.］，1998:307-313.

［5］ Tamura Y，Matsumoto Y.Improvement of bubble model for cavitating flow simulations［J］.Journal of Hydrodynamics，2009，21(1):41 -46.

［6］ Brennen C E.Cavitation and Bubble Dynamics［M］.Oxford:Oxford University Press，1995:47 -50.

［7］ Martynov S B，Mason D J，Heikal M R.Numerical simulation of cavitation flows based on their hydrodynamic similarity［J］.International Journal of Engineering Research，2006，7(3):283-296.

［8］ Hosangadi A，Ahuja V，Arunajatesan S.A generalized compressible cavitation model ［C］∥Fourth International Symposium on Cavitation.Pasadena:California Institute of Technology，2001:sessionB4.003.

［9］ ZHANG Yao，LUO Xian-wu，JI Bin，et al.A thermodynamic cavitation model for cavitating flow simulation in a wide range of water temperature ［J］.Chinese Physics Letters，2010，27 (1):016401.

［10］ LI Zhi-min，PENG Xiao-feng，LEE Du-zhong.Interfacial mass transfer around a vapor bubble during nucleate boiling［J］.Heat Mass Transfer，2004，41(1):5 -11.

［11］ 褚学森，王志，颜开.自然空化流动数值模拟中参数取值影响的研究［J］.船舶力学，2007，11(1):32 -39.CHU Xue-sen，WANG Zhi，YAN Kai.Parametric study on numerical simulation of natural cavitation flow［J］.Journal of Ship Mechanics，2007，11(1):32 -39.(in Chinese)

［12］ 魏海鹏，郭凤美，权晓波.潜射导弹表面空化特性研究［J］.宇航学报.2007，28(6):1506 -1523.WEI Hai-peng，GUO Feng-mei，QUAN Xiao-bo.Research on cavitation of submarine launched missile’s surface［J］.Journal of Astronautics，2007，28(6):1506 -1523.(in Chinese)